永磁同步电机架悬直驱机构与驱动轴的干涉分析*

罗湘萍 徐 旻 田师峤 张文超

(同济大学铁道与城市轨道交通研究院，201804，上海//第一作者，副教授)

0 引言

传统转向架的驱动电机选用异步交流电机，但异步交流电机的输出特性无法满足轮对低转速、高转矩的特点，需通过传动齿轮加以调整，从而引发驱动装置重量增加、齿轮传动噪声和能量损耗等一系列问题。

永磁同步电机直接驱动型转向架舍弃了传统转向架上电机和轮对之间的传动部件，直接将电机输出的力矩传递给车轮或车轴[1]。相对于传统的齿轮传动转向架，动力驱动系统更加简单，重量更轻，可取消变速箱，减少效率损失，降低维护量和传动噪音。同时，永磁同步电机具有功率密度大、低速输出转矩大、效率高等优点，因此将会逐步替代传统异步交流电机，进而实现传动系统的升级。

永磁同步电机有多种悬挂模式，按照直驱技术模式可分为永磁同步电机架悬直驱和永磁同步电机轴悬直驱，前者采用独立空心轴作为电机转子，电机悬挂于构架，车轴与转子空心轴间采用弹性连接，其结构图如图1所示[2]；后者采用车轴直接作为电机转子的一部分，电机直接悬挂于车轴，其结构图如图2所示[3]。目前，对于中低速的轨道车辆，国外主要采用轴悬直驱模式。而对于较高速的轨道车辆，多采用架悬直驱模式。本文的研究对象为适用于城市轨道交通系统的准高速转向架永磁同步电机架悬直驱结构。

图1 永磁同步电机架悬直驱结构图

永磁同步电机架悬直驱技术，要求轮对与电机空心轴间留有一定间隙，来适应轮对与空心轴之间的动态变位。对于城市轨道交通车辆，此动态变位主要来自空重车变化下的一系弹簧垂向静挠度改变量，轨道非线性病害冲击，以及轨道随机不平顺激励下的轮对和空心轴间动态位移。因此，永磁同步电机架悬直驱结构设计面临如下技术难点：如何实现永磁同步直驱电机和车轴的匹配，并使之在轨缝、道岔或轨道病害等非线性冲击以及轨道随机激励下不互相干涉。

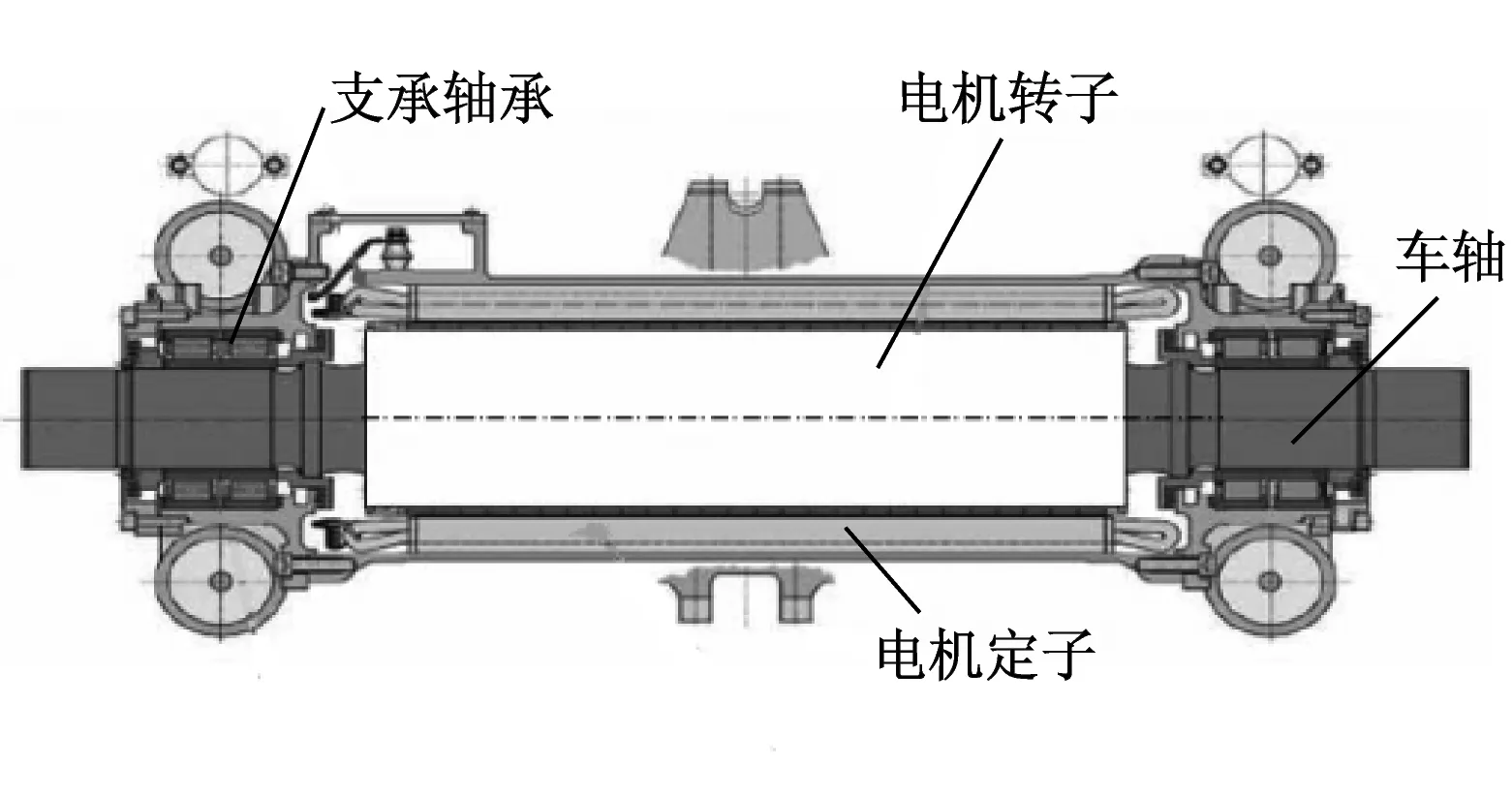
图2 永磁同步电机轴悬直驱结构图

为解决上述技术难点，分别建立永磁直驱柔性构架有限元瞬态响应分析模型及整车动力学模型，并提出架悬直驱结构与驱动轴间动态间隙的干涉评判指标，以此作为间隙大小设定的依据。

1 干涉性评判准则

图3为空心轴与车轴、电机外壳间隙示意图。图3中，Gd为空心轴与车轴以及空心轴与电机下部垂向间隙设计值，Gu为空心轴与车轴以及空心轴与电机上部垂向间隙设计值。

图3 空心轴与车轴、电机外壳间隙示意图

在下述两种工况下，若Gd、Gu分别满足式(1)、(2)的条件,则说明上述间隙值设计合理。

AW0(空载)工况：Gd≥Zi+Zr+S

(1)

AW3(超载)工况：Gu≥Zs+Zi+Zr+S

(2)

式中：

Zs——空重车一系弹簧垂向静挠度变化值；

Zi——非线性冲击下垂向动态间隙变化值；

Zr——轨道随机激励下垂向动态间隙变化值；

S——安全余量。

由式(1)可知，下部垂向间隙值未考虑空重车的变化量，其原因为城市轨道交通车辆存在的空重车变化，致使一系挠度变化较大。故为充分利用有限的间隙空间，采用驱动轴和空心轴内间隙不对称分布设计：AW0工况下，上部间隙较大，下部间隙较小，此时仅需确保驱动轴与驱动机构下部不干涉；AW3工况下，因空重车变化，转向架构架下移，导致驱动机构下移，故此时上部间隙变小，下部间隙变大，这种状态下仅需确保驱动轴与驱动机构上部不干涉。

2 非线性瞬态响应分析

2.1 非线性有限元冲击模型的建立

转向架运行在轨道线路上时，轨道病害会造成轮轨冲击，此冲击力会导致电机与空心轴、空心轴与车轴间垂向动态位移发生变化。这是一个强烈非线性的冲击过程[4-7]，因此需要建立完整的永磁架悬直驱转向架的有限元模型对其进行分析，图4所示为转向架-轨道耦合系统FEA(有限元分析)模型。

图4 转向架-轨道耦合系统FEA模型图

2.2 非线性冲击计算工况

在上述模型中，车辆转向架运行速度为140 km/h。非线性冲击子工况如表1所示。由表1中的5种子工况可排列出30个计算工况。例如，计算工况1：处于AW0状态，左轨轨缝错牙(前矮后高)，右轨无病害；计算工况30：处于AW3状态，左轨存在低接头，右轨轨缝错牙(前高后矮)。

表1 非线性冲击子工况

2.3 非线性冲击工况计算结果

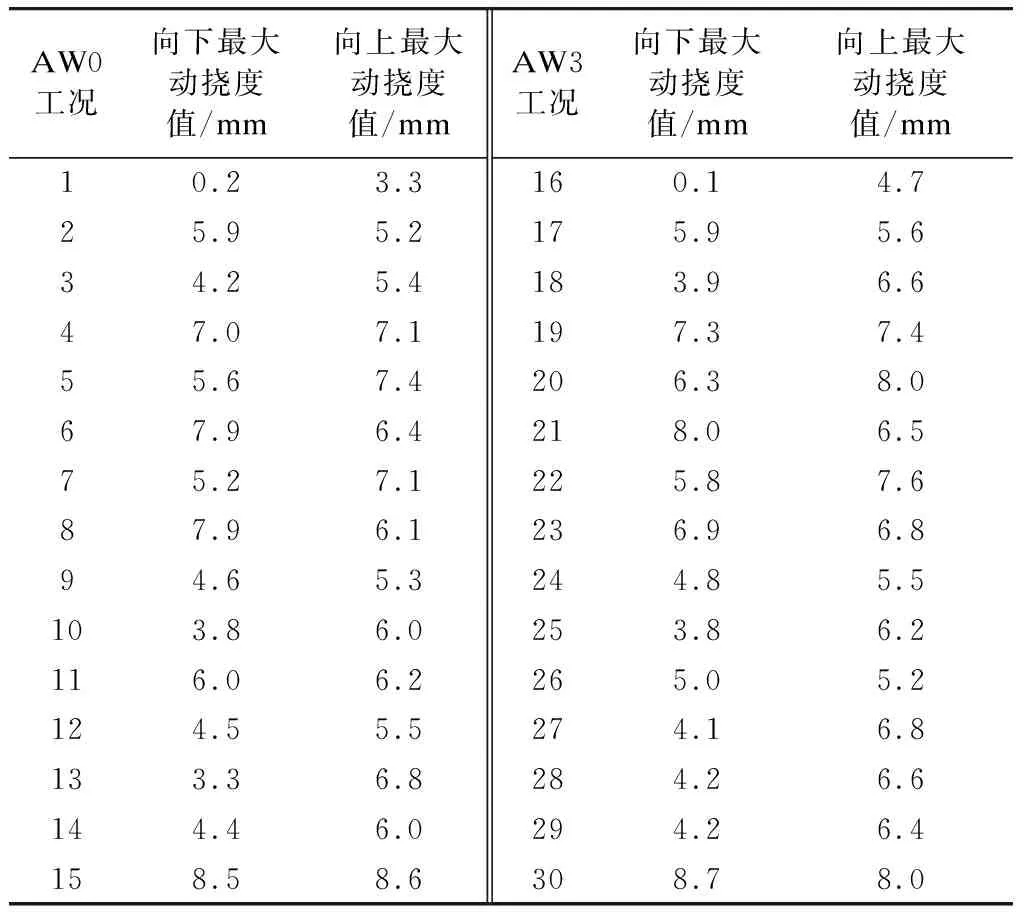
非线性冲击工况均以空心轴与车轴/电机壳体垂向相对动态位移的最大值为结果，其计算结果如表2所示。图5所示为工况29和工况30下的空心轴与车轴和电机壳体垂向相对动态位移随时间变化曲线图。

a) 工况29

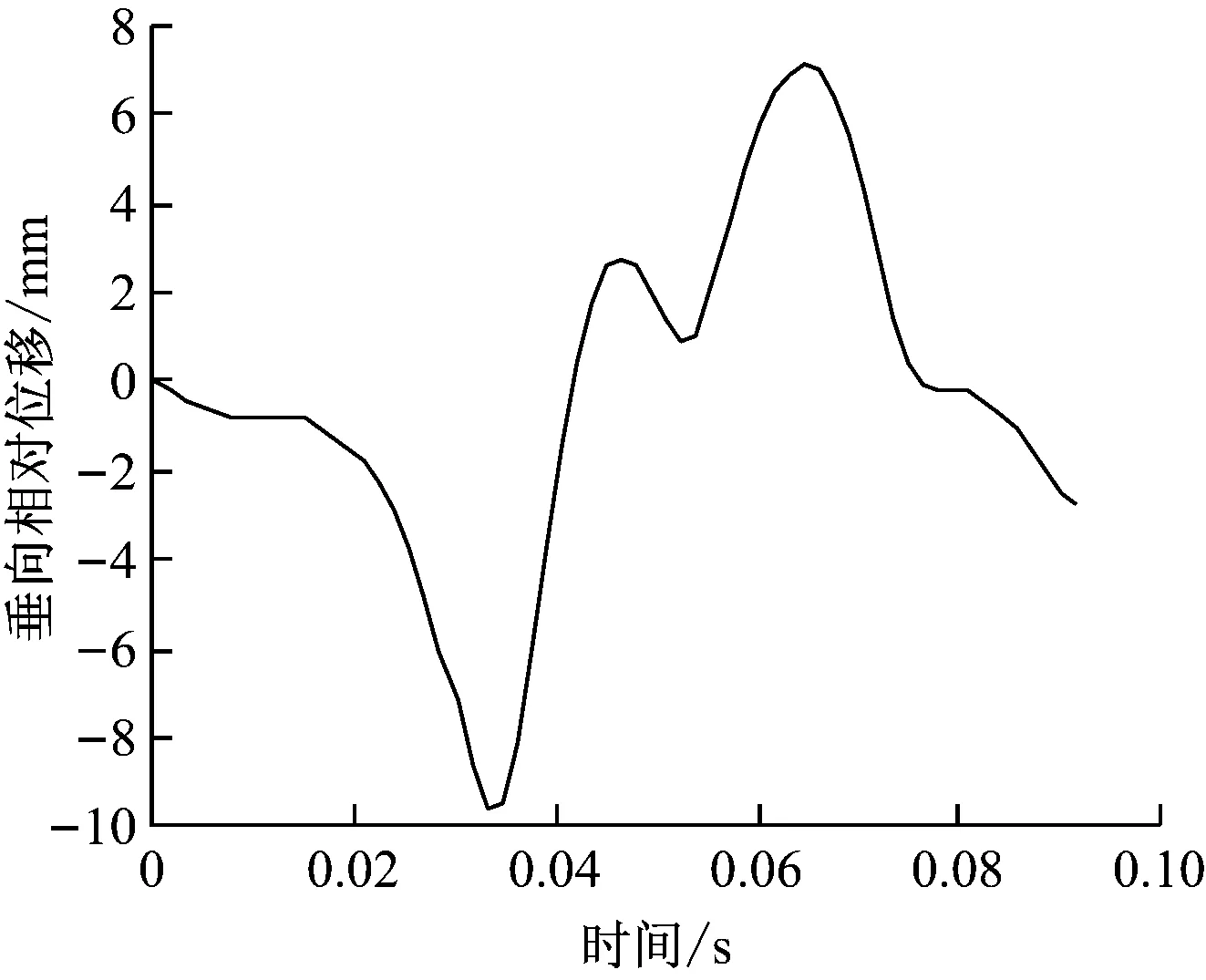
b) 工况30

AW0工况向下最大动挠度值/mm向上最大动挠度值/mmAW3工况向下最大动挠度值/mm向上最大动挠度值/mm10.23.3160.14.725.95.2175.95.634.25.4183.96.647.07.1197.37.455.67.4206.38.067.96.4218.06.575.27.1225.87.687.96.1236.96.894.65.3244.85.5103.86.0253.86.2116.06.2265.05.2124.55.5274.16.8133.36.8284.26.6144.46.0294.26.4158.58.6308.78.0

AW0工况下，轮对与空心轴间下间隙小，故此时应考察各冲击工况的向下最大动挠度值；AW3工况下，轮对与空心轴间上间隙小，故应考察各冲击工况的向上最大动挠度值。

由表2可知:AW0工况下，向下最大动挠度值为8.5 mm；AW3工况下，向上最大动挠度值为8.0 mm，两者较为接近。因为由轨道病害引起的轮轨垂向冲击力主要由簧下质量决定，故由冲击力引起的位移变化与车辆状态AW0/AW3关系不大。

3 随机响应动力学分析

利用Simpack建立配备永磁同步电机架悬直驱转向架的整车动力学模型，分析计算时，加入轨道不平顺的影响，并分别考虑直线轨道与曲线轨道两种计算工况。

随机响应动力学分析以电机与车轴的垂向相对动态位移为输出结果，并取统计学中的3倍标准差，即3σ作为边界值，各工况计算结果汇总如表3～4所示。

表3 直线轨道工况下的计算结果

表4 曲线轨道工况下的计算结果

由表3～4可知：垂向动态相对位移随着车辆运行速度的增加而增大；曲线轨道工况下，线路扭曲引起电机与车轴间存在侧滚偏角，此角度在驱动机构与车轴间附加了一定的垂向位移，故相同速度等级下，曲线轨道工况的动态相对位移值较大。上述各工况下3σ最大值为11.7 mm。

4 干涉性评判

由上述非线性瞬态响应分析及动力学仿真结果可知，车辆在140 km/h的运行速度范围内，非线性冲击动态间隙向上最大变化值Zi为8.0 mm，向下最大变化值Zi为8.5 mm，随机响应动态间隙最大变化值Zr为11.7 mm。空重车一系静挠度变化Zs可由空重车载重变化及一系垂向刚度计算得到，其值为21.2 mm。

由干涉性评判标准可知，直驱机构与驱动轴上、下垂向间隙设计值Gu、Gd应满足：

Gd=19.7+S

(3)

Gu=41.4+S

(4)

考虑一定的安全余量，并圆整上述数据可得到：驱动机构中轮对与内空心轴、内空心轴与电机垂向上空隙设计值Gd定为50 mm，垂向下空隙设计值Gu定为30 mm，以此保证车辆运行过程中直驱机构与驱动轴不发生干涉。

5 结语

本文基于非线性有限元冲击模型、整车动力学模型，分析了各工况下驱动机构与驱动轴间垂向动态相对位移的变化情况，完成了永磁同步电机架悬直驱机构与驱动轴的动态匹配与间隙设计。驱动机构中轮对与内空心轴、内空心轴与电机垂向上空隙设计值Gd定为50 mm，垂向下空隙设计值Gu定为30 mm，以此确保转向架运行过程中驱动机构与驱动轴不发生干涉，保证转向架的运行安全。本文研究结论可为永磁架悬直驱机构的工程化运用提供参考。