基于网络层次分析法与证据理论的无线闭塞中心风险评估研究*

施莉娟 王 健

(1.同济大学道路与交通工程教育部重点实验室，201804，上海；2. 同济大学交通运输工程学院，201804，上海//第一作者，讲师)

无线闭塞中心(RBC)是基于故障-安全计算机平台的信号控制系统，是CTCS-3级列控地面系统的核心设备。RBC根据所控制列车的状态，及其控制范围内的轨道占用、列车进路状态、临时限速命令、灾害防护和线路参数等信息，生成列车行车许可(MA)，并通过GSM-R无线通信系统传输给车载设备，保证其管辖范围内的列车行车安全[1]。因此，对列车运行过程的风险进行分析，继而对RBC的安全风险进行可靠有效评估具有重要意义。

现有的风险评估方法主要有定量分析和定性定量相结合分析两类。定量分析主要采用故障树、事件树、贝叶斯网络等分析法[2-4]。高速列车的故障数据比较难获得，运用定量的概率分析法难以得到理想的结果，因此，定性定量相结合的方法得到了广泛的应用。文献[5]利用ANP(网络层次分析法)与反向传播神经网络建立了安全风险评估模型，并用北京—广州高铁系统进行了验证；文献[6]运用层次分析法(AHP)和熵权法确定各个指标的权重,运用灰色模糊评价模型对京沪高速铁路行车安全性进行综合评价；文献[7]应用AHP、加权平均型综合函数和最大隶属度原则，对微机联锁系统延时建立闭塞的风险程度进行评价；文献[8]针对风险数据的不完整性和不确定性，提出基于模糊推理和模糊AHP的风险分析方法，对铁路系统的风险进行了定性和定量的分析。熵权法是利用信息的熵值来确定各项指标的权重，但是对异常数据比较敏感，某些非重要指标经此法计算出的权重可能过大。AHP可以充分利用专家知识，对各项指标进行有效赋权。然而，AHP的指标一般不超过9个，其前提条件是各指标间相互独立，在实际分析当中，这一条件有时很难满足[9]。而ANP是在AHP的基础上建立起来的，不但继承了AHP的优点，还充分考虑了同一网络层中元素之间的相互关联[10]。在风险等级的评估方面，许多学者采用模糊数学将专家的模糊评语量化，将之作为模型的输入，依据最大隶属原则，对风险进行评估[5-8]。

本文针对RBC的特点，考虑风险因素之间的影响，提出基于ANP和证据融合理论的风险评估模型，对RBC的风险等级进行评估。

1 基于APN与证据理论的风险评估模型

1.1 ANP

ANP充分考虑了同一层级之间和同一层级内不同元素之间的关联关系，其基本结构可以分为控制层和网络层，如图1所示。

图1 ANP基本结构

Wij表示元素组Ci和Cj之间元素的相对重要度矩阵。以元素组Cj的元素ejl(l=1,2，…，n)为准则，构造判断矩阵，将元素组Ci中的各元素与ejl的重要度进行比较。通过一致性检验，即得到网络元素的权重向量，从而形成矩阵Wij。例如，矩阵Wij中的第一列表示Ci中各元素相对于Cj中第一个元素的重要度归一化后的结果。如果Ci和Cj之间无影响，则Wij= 0。

Cjej1 … ejp … ejnWij=Ciei1︙eih︙eimωei1,ej1…ωei1,ejp…ωei1,ejn︙︙︙ωeih,ej1…ωeih,ejp…ωeih,ejn︙︙︙ωeim,ej1…ωeim,ejp…ωeim,ejn

同理得到其他元素组间的重要度矩阵，组成超矩阵W。然后，借用专业软件将W归一化，即可得到各元素相对于各元素组的权重。

(2)

1.2 证据融合理论

证据融合理论是通过识别框架、基本概率分配函数(BPA)和融合规则对不确定性进行描述[12]。

1.2.1 识别框架

假设需要判决某个问题，对于该问题所有的可能结果用集合Θ来表示，且Θ中的所有元素都两两互斥，则称该完备集合Θ为识别框架，可表示为Θ={θ1,θ2,…,θn}。

1.2.2 BPA

由识别框架Θ的所有子集组成的集合称为Θ的幂集，记作2Θ。基本信度分配函数是从集合2Θ到[0,1]的映射。m0(A)为A(A⊆Θ)的BPA值，表示证据对结果为A的信任程度。

1.2.3 证据融合规则

对于同一假设结果有多个证据，每个证据对该结果的信任程度可能不相同，即各个证据间存在冲突。为了解决这一问题，国内外学者提出了很多修正方法，其中就包括对不同证据设置不同的折扣系数[13]。本文采用证据距离式(式(3))来度量证据Ei和Ej间的距离，基于此构造证据间的相似度矩阵(式(4))并得到各证据的折扣系数(式(6))。

(3)

式中：

mEi——表示度量证据Ei的概率分配函数值；

mEj——表示度量证据Ej的概率分配函数值。

计算出d(Ei,Ej)后，再计算两证据之间的相似度Sij=1-d(Ei,Ej)(i,j=0,1,2，…，k)，得到相似度矩阵S。

(4)

对相似度矩阵S的每列进行求和，得到每个证据关于对应结果的支持度Ssup(Ei)：

(5)

每个证据的可信度Ccrd,i可以定义为：

(6)

式中：

Ssup(Ea)——第a个证据的支持度。

将该可信度作为每个证据的折扣系数βi代入式(7)，重新得到各证据的BPA:

(7)

式中：

m(Ei)——证据Ei的可信度；

m(Θ)——Θ的可信度；

mo(Ei)——考虑折扣系数βi的证据Ei的可信度；

mo(Θ)——考虑折扣系数βi的Θ的可信度。

最后，根据新得到的证据BPA，对多条证据进行融合，算得A(A⊆Θ)的BPA:

(8)

1.3 基于ANP与证据理论的风险评估模型

在指标体系构建完整的情况下，基于ANP与证据理论的无线闭塞中心风险的评估步骤如下：

步骤1：构建风险因素集，包括一级风险因素和二级风险因素；

步骤2：运用层次分析法，通过一致性检验，求得一级风险因素Ci的权重矩阵WCi；

步骤3：采用ANP，通过一致性检验，求得网络层二级风险因素的超矩阵，继而得出风险因素相对于上层风险因素的权重；

步骤4：由步骤2和步骤3确定二级风险因素相对于目标层的权重W；

步骤5：建立评估集和专家评语模糊集，根据专家的模糊评价，计算各专家模糊评语的隶属度以及风险因素的BPA；

步骤6：根据融合理论，融合不同专家对于同一风险因素的BPA，确定所有风险因素的BPA矩阵M；

步骤7：根据F=WM进行加权综合评价，得出分析结果。

2 实例分析

2.1 风险因素集

首先需要确定风险因素集，该集合中的因素包含了系统潜在的风险和薄弱环节。以无线闭塞中心为边界，将风险因素分为两级[14]，具体见表1。

表1 风险因素分类

2.2 基于ANP的风险因素权重

2.2.1 一级风险因素权重的确定

根据Saaty 1-9标度，依据专家评判构建判断矩阵(见表2)。通过一致性检验，得出各因素的权重。

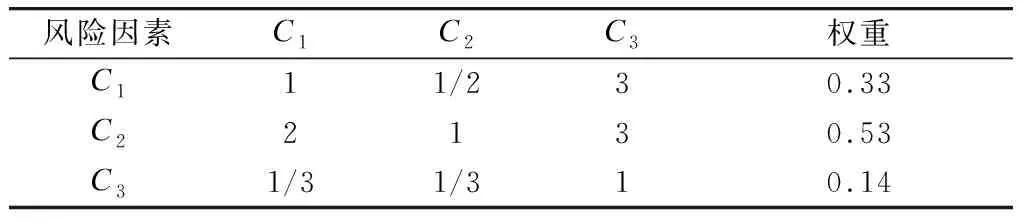
表2 一级风险因素权重判断矩阵

2.2.2 二级风险因素权重的确定

为考虑二级风险因素间的相互影响，例如，提供给RBC的原始线路数据错误(e13)，最后将生成的错误静态速度曲线发送给了车载设备，因此，采用ANP来确定二级风险因素的权重。计算过程以“数据及系统资源错误(C1)”为例，构造风险因素比较判断矩阵(见表3—表6)，进而确定风险因素的权重。

表3 二级风险因素e11下的权重判断矩阵

表4 二级风险因素e12下的权重判断矩阵

表5 二级风险因素e13下的权重判断矩阵

表6 二级风险因素e14下的权重判断矩阵

由以上4个矩阵得到C1的超矩阵子块：

对C2和C3进行同样的计算，得到C2和C3的超矩阵子块：

由于C1、C2和C3相互独立，故Wi j= 0(i≠j)。Wi j组成的超矩阵经专业软件Super Decision计算，得到加权超矩阵(见表7)。表中每一行表示二级风险因素相对于一级风险因素的权重，则对于目标层的权重为：

W=[WC1×[We11,We12,We13,We14],Wc2×[We21,We22,We23,We24],Wc3×[We31,We32,We33]]=[0.036, 0.138, 0.095, 0.061, 0.214, 0.182, 0.049, 0.085, 0.056, 0.024, 0.060]

2.3 基于证据理论的风险因素BPA函数

2.3.1 构建评估集和专家模糊评语集

本文采用证据理论，需要专家根据自身所掌握知识对某一事件做出评价，同时引入评估集和专家模糊评语集概念。

表7 二级风险因素相对于一级风险因素的加权超限超矩阵

评估集是对评估对象风险等级的划分的集合，参照国家标准GB/T 21562对风险等级的划分标准,风险共分为4级，即FR={R1,R2,R3,R4}={可忽略的，容许的，不希望的，不容许的}，对应于证据理论中的识别框架。

专家模糊评语是指专家根据自身经验，对风险发生的频度进行判断。为了更符合表达方式并且灵活地表达专家的评语，依据GB/T 21562对危害事件的发生频率的划分，定义专家模糊评语集U={u1,u2,…,u6}={几乎不可能,极少,很少,有时，经常,频繁}，对应于证据理论中的证据。

语言变量需要通过一定的规则转换成数字，即构建隶属度函数。表8和表9分别为风险等级和专家模糊评语的6元组隶属度函数[15]。

表8 风险等级隶属度函数

采用公式(9)将专家模糊评语集中元素ul映射到风险等级评估集R的各个风险等级，然后再进行归一化处理。

(9)

式中：

k——元组，k=1,2,3,4,5,6；

μk,Rh——元组k对于风险等级Rh的隶属度；

μk,ul——元组k对于专家模糊评语ul的隶属度。

2.3.2 确定风险因素BPA函数

表10为专家对二级风险因素的模糊评语表。

表10 专家对二级风险因素的模糊评语表

2.3.2.1 证据BPA函数计算

专家1对e11的评价为u1,运用式(7)计算该证据对于各个风险等级的隶属度，进行归一化，得me111=(0.928 6，0.071 4，0，0)。同理，可得出其他专家对于对e11的模糊评语隶属于各个风险等级的程度，用矩阵T表示。

2.3.2.2 证据折扣及证据融合计算

由于不同专家之间的意见不同，需要将专家的意见作为证据进行证据融合。融合证据之前，运用式(5)—式(7)计算折扣后的证据BPA,再运用式(8)对各证据的BPA进行融合。

根据式(5)和式(6)，计算得到各专家证据的支持度和折扣系数：

根据式(7)，计算得到折扣后风险因素的BPA：

T0=βi×T=

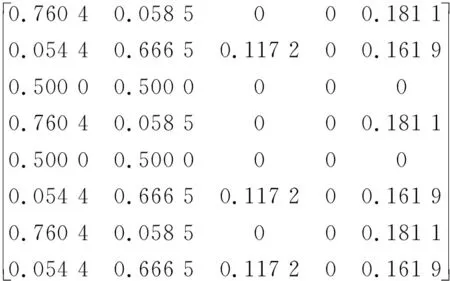
运用式(8)融合8位专家的证据，计算得出8位专家对于风险因素e11所所隶属风险等级的BPA：me11=(0.544 4，0.455 6，0，0，0)。同理算得其他风险因素所隶属风险等级的BPA，组成矩阵M。

2.4 风险评估

根据确定的风险因素权重W和各风险因素所隶属风险等级的BPA，RBC的评估结果F=WM=(0.384 9，0.615 1，0，0，0)。根据最大隶属原则，该RBC所处风险等级为R2。由矩阵M可知，收到错误的TSRS命令(e23)、收到错误的CBI紧急区域消息(e24)、TSRS状态发生变化(e31)、与ATP通信中断(e32)处在R2级的可能性超过0.99。虽然说是容许的，但是要进行重点防范。

3 结语

本文根据RBC的特点，提出了ANP和证据理论的风险评估模型。将风险因素分为3个大类、11个小类，通过ANP分析风险因素的权重，充分考虑了风险因素之间的相互影响。通过计算折扣证据理论，在降低专家意见主观性的同时，实现对专家不同意见的有效融合。通过实例分析，验证了模型良好的适应性，该评估模型亦可用于其他信号系统。