基于遗传优化算法的城市轨道交通多列车运行节能计算方法*
周翔翔 刘鑫荣 张 永 李海玉
(1. 南京理工大学自动化学院,210094,南京; 2. 广州地铁国家工程实验室, 510330, 广州∥第一作者,硕士研究生)
0 引言
城市轨道交通系统是较为复杂的多目标、多列车动态系统,且列车在该系统的运行过程中存在频繁的能量交换[1]。单车运行时,列车仅考虑在区间运行的状况,无须考虑其他车的影响以及在每个站停车时间的影响[2]。然而列车节能最重要的是制动能量的回收利用。因此,对多列车运行时的节能研究对提高能源利用率具重要的现实意义。
国内外专家对地铁多列车的节能优化已经有了一定的研究。文献[3]以广州地铁1号线为例,对正线运行过程中的列车进行能耗分析,研究了再生制动能量利用的过程,表明行车密度较大时,制动能量回收利用的效率是非常可观的。文献[4]引入乘客满意度概念,通过改变列车发车间隔研究全局能耗,并将最优方案绘制成运行图。文献[5]建立了以能耗成本、碳排放量、列车运行时间为优化目标的单线多列车调度模型,并采用多目标模糊优化算法进行求解。文献[6]研究了基于富裕时间分配方案的站间运行时间优化原理,该优化方案以总能耗为目标函数,对富裕时间进行了合理优化。以上研究对多列车节能运行均做出了巨大贡献,但在通用性和收敛速度方面仍存在着一定的缺陷。
本文提出一种基于遗传优化算法的多列车运行节能研究方法,并以我国某地铁线路4个区间组成的短线进行多列车列车节能仿真分析,优化得到停站时间和发车间隔时间。结论可为多列车节能运行提供有效指导。
1 多列车能量利用原理
多列车节能可以分为同向列车制动能量回收利用和对向列车制动能量回收利用[7]。由于同向行驶的两辆列车相隔较远,且一般处于不同的供电区间内,当远距离输送制动能量时会产生大量线路损耗,造成制动能量不能有效利用,因此本文仅讨论对向列车行驶的情况。对向列车行驶情况分为两种:一种是上行列车制动、下行列车牵引(见图1);另外一种是上行列车牵引、下行列车制动(见图2)。列车制动能量利用距离较近,一般处于同一供电站内,且制动能量利用率较高。

注:箭头所指示方向为列车运行方向
图1 对向列车行驶情况一(上行制动、下行牵引)
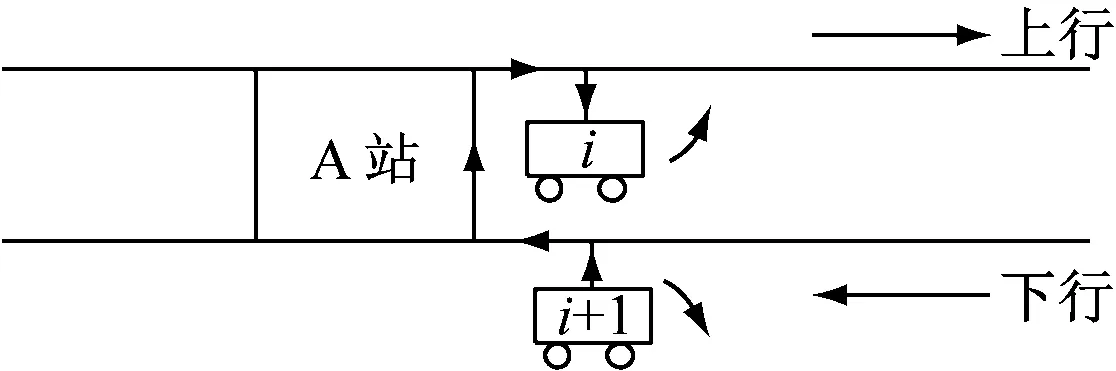
图2 对向列车行驶情况二(上行牵引、下行制动)
2 多列车运行约束条件与优化目标函数
2.1 多列车运行约束条件
综合考虑各方面可能影响多列车运行的因素,选取发车间隔、停站时间、旅行时间和安全距离等多个重要的约束条件进行分析。
2.1.1 发车间隔约束
由于每列车的“速度-距离”曲线都是固定的,因此对列车运行影响最大的就是发车间隔,发车间隔过大或过小都会引起严重的后果。按照客流特点,该地铁线路全天列车运营主要分为早/晚低峰、次高峰、早/晚高峰和正常峰6个部分,具体情况如图3所示。将06:00—07:00、22:00—24:00的早晚低峰段发车间隔定为Hthrough,将白天正常峰的发车间隔定为Hnormal,将07:00—09:00、17:00—19:00的早/晚高峰段发车间隔定为Hpeak1,将09:00—10:00的次高峰发车间隔定为Hpeak2,单位均为s。
按照该地铁线路的运行规划,列车的最小、最大发车间隔分别为Hmin、Hmax,则:
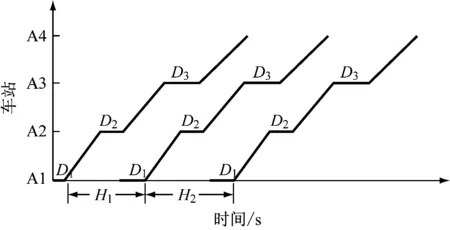
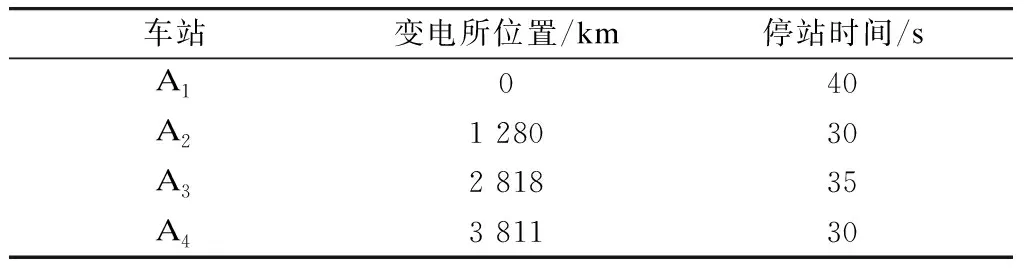
Hmin (1) 图3 某地铁线路全天列车运营分布图 此外,列车全天的出行对数Npair是一个固定值,则: (2) 2.1.2 列车停站时间约束 列车的停站时间由开门时间、乘客上下车时间和关门时间3部分组成[8]。停站时间越长,车站的通行能力越强。停站时间较短时,乘客前往目的地的旅行时间可能会变长,并极有可能引起推搡事故。因此,每个车站的停站时间应根据年平均客流量进行初步限制,为每个车站做出参考的停站时间范围,且停站时间要求为5 s的整倍数。设车站编号为1,2,3,…,i,…,N,则每个车站对应的停站时间为D1,D2,D3,…,Di,…,DN。 第i个车站的停站时间下限为Di,min,停站时间上限为Di,max,则每个车站的停站时间约束为: Di,min≤Di≤Di,max (3) Di%5=0 (4) 式(5)为取余运算。 2.2.1 多列车运行能耗目标 在城市轨道交通系统中,不仅列车消耗电能,而且由于接触网和导轨有电阻的存在,同样会消耗能量[9]。尤其在线路运行高峰期,由于负荷较大,供电电流较大,则线损亦比较大。因此,多列车运行的能耗目标要综合考虑线路的损耗和列车的能量消耗。以所有牵引变电所发出的能量总额为目标,设全线牵引变电所的编号为P=[P1,P2,P3,…,Pi,…,PN],Pi站的电压和电流分别为UPi和IPi,对应的能耗为EPi,则列车全天的能耗量为: (5) 2.2.2 多列车运行旅行时间目标 列车旅行时间是指列车从始发站开始出发到从终点站退出运行的所有时间之和,过长的旅行时间则预示线路中可能发生延误现象[10]。在日常管理中,允许实际旅行时间与规定运行时间存在很小的误差。设列车在线路中的停站时间为D=[D1,D2,…,Di,…,DN](N为车站总数),列车在每个区间的运行时间为t=[t1,2,t2,3,…,t(N-1),N],则得到列车运行的旅行时间目标为: (6) 本文优化的目标是建立一个最优的时刻表,该时刻表需要满足: (1)分别针对高峰期和非高峰期的发车间隔进行优化,高峰期的发车间隔误差为±10 s,非高峰期发车间隔的误差为±30 s。 (2)停站时间的误差为±5 s。 (3)列车单程运行时间和全天运行时间等其他配置均保持不变。 (4)优化过程应同时考虑列车运行能耗和再生制动能量,并计算得到两者的平衡点,以求达到全局(变电站)能量最优。 根据多列车运行的约束条件和优化目标,建立以下多列车优化模型: min{Em,ΔT} (7) 其中,Npair代表一天中整条线路的发车对数;ΔT=|Ttable-Ttravel|,Ttable代表计划时刻表规定的运行时间。 在多列车优化模型中,需要建立地铁线路全天的列车运行时刻表。列车运行时刻表由两方面组成,一是单列车在各站台的停站时间,另一个是每列车之间的发车间隔[11]。本文采用遗传算法对多列车运行优化进行求解。地铁线路全天停站时间和发车间隔示意如图4所示。 注:H1为第一车与第二辆车之间的发车间隔;H2为第二辆车与第三辆车之间的发车间隔;A1,A2,A3,A4表示线路区间的4个车站 图4 某地铁线路停站时间和发车间隔示意图 采用遗传算法对列车运行时刻表进行优化的步骤如下: (1)编码:根据实际线路的站台数,将列车在各站的停站时间序列D=[D1,D2,D3,…,Di,…,DN]和发车间隔H= Hpeak1,Hpeak2,Hnormal,Hthrough 进行综合编码,即定义遗传算法的染色体为 C=[D1,D2,D3,…,Di,…DN,Hpeak1,Hpeak2,Hnormal,Hthrough 。按照实际需求,D大多处于30~60 s范围内;而发车间隔H在高峰段约为120~300 s,在低峰段约为180~600 s。由此可确定基因的长度,并相应随机选择50个个体组成种群。 (2)将种群中的50组解分别带入目标函数,得到全天的列车运行时刻表。计算出列车的全天能耗、变电站负载数据以及列车旅行时间,并将运行结果代入适应度函数,得到每组解的适应值。 (3)根据适应度值,对种群中的50组解排序,并进行遗传操作得到新一代的包含50组全新可行解的种群。其中,交叉和突变的比率分别为0.8和0.005。 (4)重复步骤(2)和步骤(3),直到计算出的可行解满足下列两个条件之一:①两代种群的最佳适应度值相差0.001以内;②种群总数不超过50代。 为了满足能耗越小、旅行时间差越小和个体适应度越大的需要,选择以下适应度函数Fit进行多列车遗传优化算法的研究: (8) 式中: A,B,C,D——常数。 为了验证多列车节能计算模型的准确性,本文以某地铁线路4站3区间进行仿真分析。其中,线路区间牵引变电所位置及各站停站时间如表1所示。 表1 某地铁线路区间牵引变电所位置及各站停站时间 地铁线路采用第三轨供电,额定电压等级为750 V,第三轨单位电阻率取0.125 Ω/km,钢轨电阻率取0.02 Ω/km。根据单列车运行节能仿真模型,求出列车在3个区间的距离曲线和功率曲线,作为多列车运行的输入。每个车站的停站时间调整为±5 s或者保持不变。仿真运行时间设置为2 h。列车在第一个小时内的发车间隔为420~450 s,在第二个小时内的发车间隔为540~570 s。 首先,在第一小时内发车间隔为450 s,在第二个小时内发车间隔为550 s,停站时间序列为[40,30,35,30] s时,只有1/4的重叠能够实现制动能量内的有效利用。在使用多列车运行节能优化后,前端最优解为:列车在第一小时内发车间隔调整为463 s,在第二小时内发车间隔调整为556 s,停站时间序列调整为[35,35,40,25] s。在 2 h的仿真时间中,有3/4可以产生制动能量的有效利用。优化前后的区间能耗结果如表2所示。 表2 优化前后区间能耗表 由于仿真区间较短,所受限制较少,多列车节能优化仿真效果明显。时刻表优化前后,全线运行时间442 s维持不变,列车能耗下降约7.87%,线路损耗下降约29.21%,全线能耗下降约8.23%。优化后,由于线路中电流无较大范围内的波动,线路损耗下降较多,且列车能够有效地使用制动能量,从而降低全线损耗。 本文提出一种基于遗传优化算法的多列车运行节能研究,并根据列车制动能量利用的原理对多列车运行的多目标优化问题进行求解。以我国某地铁线路3个区间组成的短线进行多列车节能仿真,优化得到各站停站时间和发车间隔。仿真结果表明,通过调整停站时间和发车间隔,能够有效地降低全线能耗,从而肯定了多列车节能计算中的优化模型和遗传算法的合理性。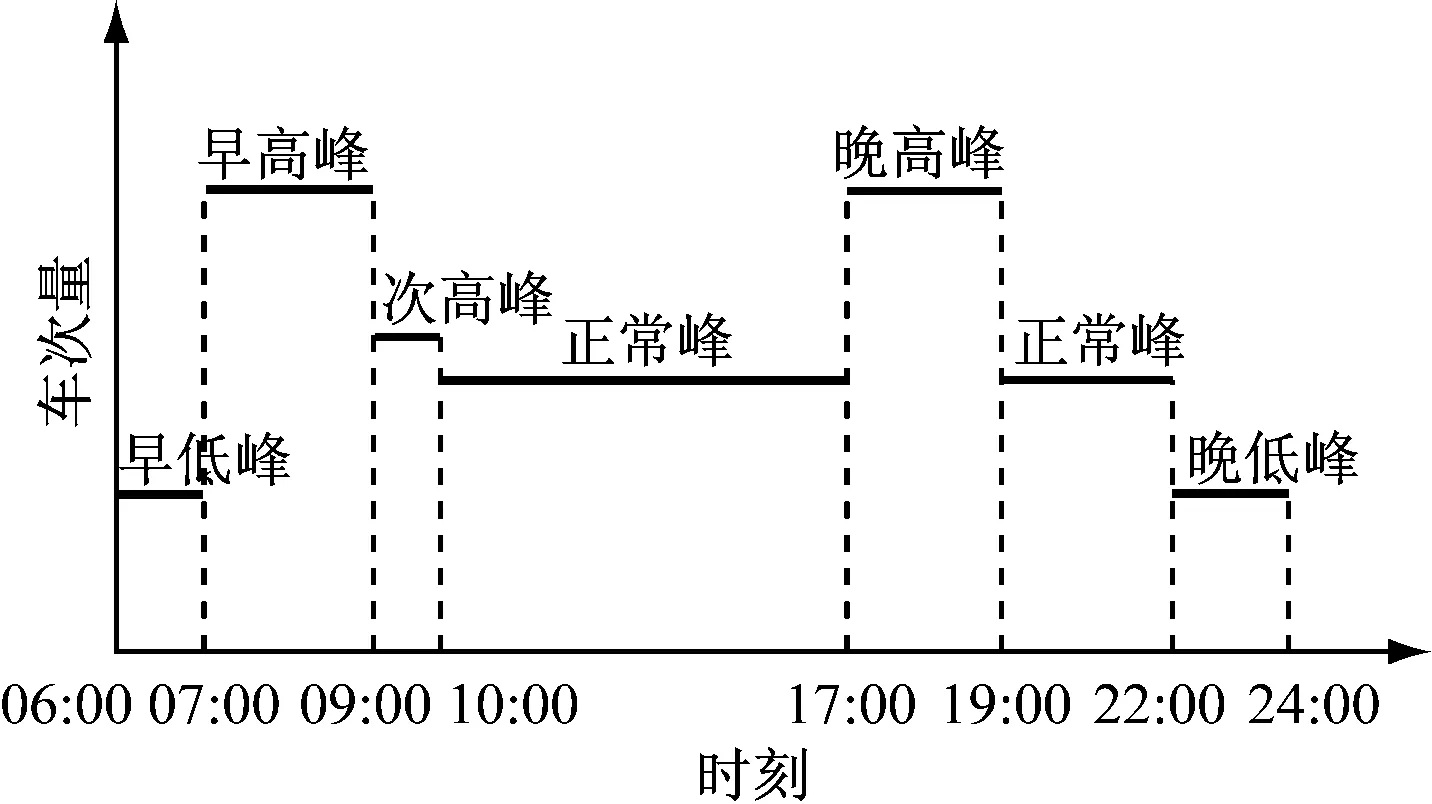

2.2 多列车优化目标函数
2.3 多列车运行多目标优化模型
3 基于遗传算法的模型求解




4 仿真分析
4.1 仿真背景
4.2 仿真结果

5 结语

