长方体变形记

刘善娜（特级教师）

【教学时机】

人教版五年级下册，《长方体、正方体的表面积》《体积》学习之后。

【教学目标】

1.通过画多个叠加的长方体草图，让学生掌握“虚”“实”画法，提升利用几何直观解题的能力。

2.使学生进一步感受面与体的变化，培养其空间观念。

【教学过程】

一、方法回顾

师：之前，我们画过在一个长方体的基础上添加一个长方体的草图，画法上要注意什么？

（板书：前面→上面→侧面，标注数据）

师：先画一个棱长为2厘米的正方体草图，再在其右侧添加一个同样大小的正方体，拼成一个长方体。你能提出并解决哪些问题？

（板书：减少的面；表面积；体积）

【设计意图：回顾基本画法，然后画正方体叠加图，关注数据的标注和问题解决意识的培养。】

二、以练推进

师：今天，我们要画更加有难度的草图。

1.画五个棱长为2厘米的正方体，拼成一个长方体。

（1）尝试画图。

（2）反馈交流。

反馈一：依次添加。

反馈二：一次构图。

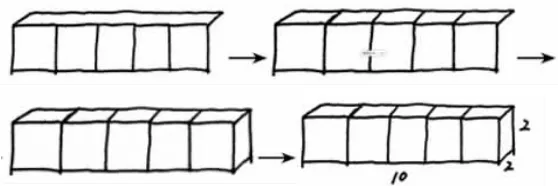
问1：大家对他们所画的草图有什么看法呢？

问2：草图需要标注数据，要标注清楚什么数据？

小结：一次性构图画起来更快、更方便，依次添加正方体画起来麻烦，但“减少的面”很清楚。标注数据，要关注图形的基本数据，如正方体的棱长、长方体的长、宽、高。

问3：根据这个草图和标注的数据，你能提出并解决哪些问题？请口头解答。

问4：五个正方体还能拼出其他形状的长方体吗？

【设计意图：通过两种画法比较，引导学生关注基本数据的标注，掌握合理、简洁的画法；通过提问与解答，让学生进一步感受草图对解题的助力；教师追问“还能拼出其他形状的长方体吗？”进一步培养学生的空间观念。】

（过渡：拼不出了，那就来用长方体拼）

2.有两个长21厘米、宽15厘米、高1厘米的长方体，要拼成一个大长方体。拼成的大长方体的表面积、体积分别是多少？

（1）解读问题。

师：你从条件和问题中读懂了什么？

小结：拼法不止一种，答案不止一个。

（2）想象拼法。

师：先想象一下，这两个小长方体大概什么样子？类似于什么物体的形状？（厚笔记本）你认为有几种拼法？

（3）尝试画图。

师：请画出三种拼法的草图，再解决问题。

（4）反馈交流。

第一种拼法：

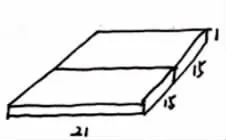
第二种拼法：

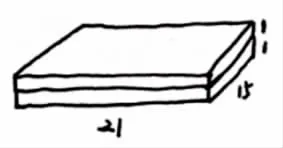
第三种拼法：

问1：说说每一种拼法怎样画最方便？（师生讨论，教师示范，学生跟着再画一次）

小结：露的多的面先画。前后拼时前面的长方体先画，上下拼时上面的长方体先画，左右拼时右边的长方体先画。（如果画线条习惯于从左往右，左边的先画也可以）

问2：哪一种拼法的表面积最大？哪一种最小？为什么？

（先指着草图说明，再关联式子：原先两个长方体的表面积的和－拼合面的面积=现在的表面积）

问3：体积为什么不变？

问4：草图上标注的基本数据有什么用处？

问5：在拼的过程中，得到的新的长方体的表面积和体积有什么特点？

小结：立体图形的不同拼组方式，表面积会发生变化，但体积不会变。

（5）体会用草图解决问题的优点。

师：说说画草图解决问题的好处在哪里？

（过渡：通过画草图我们轻松地解决了类似两本厚笔记本相关的表面积、体积问题，那如果现在有50本笔记本呢？）

3.有50本长21厘米、宽15厘米、高1厘米的厚笔记本，要打包寄送，怎样包装所用的包装纸最少？（连接重叠处忽略不计）

（1）解读信息与问题。

师：这是求表面积最少的问题。

（2）讨论方法。

问1：要先确定如何打包表面积最少吗？

问2：确定了全部是上、下面叠加后，请画草图找到新的长方体的长、宽、高，看谁画的草图能帮助自己快速找到准确的基本数据。

（3）草图展示。

展示一：

展示二：

问1：说说你是怎么画的，怎么想？

问2：这两个草图都能让我们找到基本数据，对此你有什么想说的？

小结：草图中具体个数的数据不一定都要画完整，画一部分想一部分，能帮助我们找到需要的数据，画草图的目的就达到了。

【设计意图：通过增大数据，让学生感受到画数学草图不似美术作图，画数学草图的目的是帮助自己解决问题、找到基本数据，因此要用上一些推理等方法，简洁作图，能找到关键信息即可，不必画出所有细节。】

三、拓展延伸

1.把一个长方体的高增加2厘米，它就变成了正方体，表面积增加了40平方厘米。原来的长方体体积是多少立方厘米？

2.快递公司要邮寄20本《现代汉语词典》，每本词典长25厘米，宽15厘米，厚3厘米。如果打包成一包邮寄，该怎么包？请你画一个草图，并标上数据。算一算需要包装纸多少平方分米？（连接重叠处忽略不计，材料越省越好）

【教学建议】

本节课是学生在充分掌握了长方体表面积、体积的基本概念，会做基本练习后适合学习的内容。学生经由此课学习，会在原有的画草图经验上生发技巧，提升解决相对抽象的、较难的表面积、体积问题的能力，本课也可以视为一节练习课。本节课的学习素材就是将物体“打包”，在实际教学中要凸显两个重点：

一、充分感受变化中的“不变”

几个立体图形拼合切割，会导致表面积发生增减变化。学生遇到这些变化，常常会觉得束手无策，出现大量的错题。这节课中，要教学生利用作图以“不变”应“万变”。不管怎么变化，长方体和正方体的表面积计算公式不会变，那么，就要有在各种“变化”的信息中去寻找基本数据——长、宽、高或者棱长的意识。在画图的过程中，要重点引导学生养成寻找并标出长、宽、高或者棱长的习惯，感受万变不离其宗之妙。

二、草图不一定要完整，但要有助于基本数据的确定

有些数学问题中蕴含较大的数据，如果画图时要完整呈现的话，既耗费时间又给学生增加了难度。“画数学”的“画”是培养学生的空间想象能力，只要“画”到能帮助自己找出基本数据即可。一半画 ，一半想象，长、宽、高都标注出来了，长方体表面积的问题也就迎刃而解。教学中，要让学生充分认识到自己画图的目的，理解草图的“合理性”与“简洁性”，学会在草图中寻找关键信息，力争让学生通过草图提升几何直观能力。