空间碎片环境的长期演化建模方法

张育林，张斌斌，王兆魁

(1. 国防科学技术大学空天科学学院，长沙 410073；2. 清华大学航天航空学院，北京 100084)

0 引 言

空间碎片环境是在人类航天事业发展过程中才逐渐形成的一类“人造”空间环境，是由大量空间碎片构成的。根据美国空间监视网的观测数据，截至2016年仍在轨运行的空间目标超过17000个，而在轨运行的编目目标中，近90%是空间碎片[1]。由于空间碎片的运动是无控且很难精确预测的，碎片一旦与航天器相撞，将会引起航天器故障甚至会使航天器解体，给航天器在轨运行带来巨大威胁。历史上已经发生多次航天器被空间碎片撞击的事件[2-3]，如1991年俄罗斯COSMOS 1934卫星被一个碎片撞击，导致卫星部分解体；2009年美国Iridium 33卫星和一个大的完整空间碎片——俄罗斯失效的通信卫星COSMOS 2251相撞，直接导致两个卫星解体，产生近2000个编目解体碎片和大量未编目的碎片[4]。另外，还有10起以上已经确认由空间碎片碰撞而引起的航天器失效或故障事件[5]。空间碎片环境已经对人类航天活动已产生严重的影响。

随着空间碎片规模的持续增加，空间碎片环境带来的空间安全问题日益突出。对碎片环境的长期演化趋势进行预测和分析，获取碎片碎片环境演化的内在机理和整体分布指标，则是开展碎片环境评估以及制定碎片环境减缓策略的重要基础[6]。早在1978年，Kessler和Cour-Palais等人，通过分析空间目标的相互碰撞作用，建立描述空间碎片数量变化的数学模型[7]，对碎片的增长趋势进行分析。近些年，碎片环境演化建模研究的工作得到了快速发展。根据演化模型选取的演化状态量，可将演化模型可分为两类[8]：

一类是以宏观状态量为变量的整体演化模型。利用宏观量作为描述碎片演化的状态量，如碎片在空间中的分布密度、碎片的数量等，建立碎片环境整体演化模型，利用解析或数值方法得到碎片环境的长期演化规律。Rossi[9]、Telant[10]、Lewis[11]、Nazarenko[12]以及Kebschull[13]等人在整体演化模型方面开展了研究。当选取空间碎片数量作为状态量时，利用常微分方程(组)建立演化模型，能够得到碎片数量的长期增长趋势；当选取空间密度作为状态量时，利用偏微分方程(组)建立演化模型，能够给出碎片在空间中的演化分布趋势。由于选取宏观量描述碎片的演化状态，不跟踪单个碎片的运动状态，演化效率通常较高。另一方面，由于对碎片环境的演化进行了理想的近似假设，限制了整体演化模型结果的精度。如上述模型中，Rossi等人假设碎片运行在圆轨道上。整体演化模型中碎片受到的作用力模型一般较为简单，如Rossi、Letizia等人在建立整体模型时仅考虑了大气阻力作用。

另一类是以单个碎片的运动状态为变量的演化模型。如低地球轨道到地球静止轨道(GEO)环境的碎片模型(LEGEND)[14]、流星体和空间碎片环境参考模型(MASTER)[15]、空间碎片减缓长期分析模型(SDM)[16]、地球碎片环境演化模型(MEDEE)[17]、地球同步轨道碎片环境分析和监视模型(DAMAGE)[18]以及长期碰撞分析工具(LUCA，LUCA-2)[19]等。上述模型中，首先利用确定性或随机性方法，建立摄动力作用、航天发射活动、空间目标的相互碰撞解体以及在轨目标爆炸解体等影响因素的计算模型；再利用轨道更新计算方法，不断对碎片的运动状态进行推演，从而得到碎片环境的长期演化结果。通过跟踪单个碎片的运动状态，可以建立精确的力学模型来确定碎片的运动状态。但跟踪每一个空间碎片的运动状态，当碎片规模不断增加时，需要消耗大量的计算资源才能得到碎片环境的长期演化结果。对于空间目标相互碰撞事件、目标在轨爆炸事件，一般通过蒙特卡罗随机仿真的方法实现。基于上述模型运行得到的一次演化计算结果只是众多随机结果的一种可能，需要在多次计算结果的基础上，统计得到期望的演化结果，这进一步提高了对演化计算资源的需求。因此，针对影响碎片环境演化的复杂因素，在建立精确可靠的计算模型的条件下，进一步设计高效的演化计算方法，是跟踪单个碎片的运动状态，构建碎片环境演化计算模型的关键。

本文针对空间碎片环境的演化建模问题，从宏观和微观两个方面，分别构建了碎片环境的整体演化模型和数值演化计算模型。通过对比两种模型的长期演化结果，分析了两种模型的特点和适用条件。利用演化模型的结果，讨论了碎片环境的长期演化趋势和稳定性。

1 空间碎片环境长期演化建模

1.1 分层离散化演化模型

针对低地球轨道碎片碎片环境，以碎片空间密度作为描述碎片环境分布状态的宏观量，考虑影响碎片环境演化的主要影响因素，建立空间碎片环境整体演化动力学方程。

首先，将碎片分布空间分层离散化。根据当前编目目标的运动状态[1]，近90%以上的编目目标运行在圆轨道上。且圆轨道目标解体产生的碎片中绝大部分运行在圆轨道上。为了方便讨论，假设空间碎片均运行在圆轨道上，且碎片为匀质球形。可将近地轨道上的空间碎片划分到Nh高度层内。在摄动力作用下，认为空间碎片在同一个高度层内是均匀分布的[9, 20]。为了体现大气阻力对碎片环境的影响，进一步将同一个高度层内的碎片，按照其尺寸大小划分到Na个面质比区间内。综上，我们可以将空间碎片分成Nh×Na个碎片组。

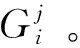
(1)

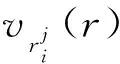
(2)

式中：(A/m)j是第j个面质比区间的平均面质比；ri0和Hi分别是第i个高度层的参考地心距和密度标高；ρi0是ri0处的参考大气密度。对于不同高度层，ri0、ρi0和Hi取值不同，可以通过查表获取，如参考文献[21]。

为了简化，进一步将式(2)中的系数定义为：

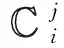
(3)

(4)

(5)

(6)

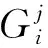
(7)

将方程(4)和(5)代入到约束控制方程(1)中，并令Δr足够小，即令Δr→0，可以得到微分形式的分层离散化模型：

i=1,2,…,Nhj=1,2,…,Na

(8)

求解模型(8)中包含的Nh×Na个偏微分方程组，得到低地球轨道上空间碎片的长期演化结果。

1.2 空间碎片环境的长期演化计算模型

通过跟踪逐个碎片的运动状态，建立碎片演化过程中的摄动力作用、目标之间相互碰撞解体、航天发射活动等影响因素的计算模型，在高效数值计算方法的基础上，构建碎片环境的长期演化计算模型。长期演化计算模型的基本框架如图2所示。

图2中目标爆炸解体、目标相互碰撞解体以及人类的航天发射活动等会引起空间碎片规模不断增加；而碎片在空间运动过程中的受力，尤其大气阻力的作用，会引起碎片运行轨道高度降低，最终导致碎片再入大气层销毁。在多种影响因素综合作用下，空间碎片数量将随时间不断动态变化。

长期演化计算模型中考虑的摄动力因素包括：大气阻力，采用Harris-Priester模型计算大气密度；基于4×4阶重力场模型确定的地球非球形摄动；太阳、月球引力摄动；太阳光压摄动。上述摄动力计算模型是在综合计算精度和复杂度的基础上确定的，确保能够反映碎片环境长期分布规律，且具有较高的计算效率。

空间目标之间剧烈的碰撞作用会导致目标解体，产生大量的解体碎片，严重影响着空间碎片环境的长期演化。对空间碎片环境演化过程的碰撞事件进行建模研究，包含两个方面，一方面是建立碰撞概率计算模型，确定演化过程可能发生碰撞的空间目标；另一方面是建立目标解体产生碎片的模拟方法，产生目标解体碎片。在确定目标之间发生碰撞的概率时，借鉴“立方体”碰撞概率模型[24]的离散化空间思想，即将空间碎片分布的空间划分成离散的空间体积元，在每个体积元内确定目标相互碰撞的概率。如图3所示，沿着地心距、赤经和赤纬方向，分别按照间隔Δh、Δλ和Δφ，将碎片分布空间划分成若干空间体积元。空间体积元Ci,j,k定义为：

(9)

式中(ri,λj,φk)是体积元Ci,j,k中心的球坐标。

对于碎片环境演化过程的某一时刻，当一个体积元目标数量大于1个时，通过对两两目标之间的相对运动状态进行，确定碰撞概率。定义垂直于相对运动速度矢量的平面为相遇平面，在相遇平面内将碰撞概率计算转化为二维平面概率密度积分问题，进一步利用级数展开得到近似的解析解[25-26]。记同一个体积元内两目标的碰撞概率为PC，则

(10)

式中:u和v分别定义为

(11)

由于式(10)具有解析的表达式，提高了大规模空间目标之间的碰撞概率的计算效率。确定目标之间发生碰撞的概率后，可进一步利用NASA标准解体模型，通过随机抽样方法确定两目标是否发生碰撞。

航天发射活动是导致空间大尺寸目标增加的唯一原因，是产生大量空间碎片的物质基础，对碎片环境的演化产生着重要影响。发射率L定义为每年发射入轨的航天数量，可用下式确定：

L=f(t,h)

(12)

式中:t是时间，单位是年；h是高度。对于给定的时刻和高度，L可取常值，也可依据历史发射任务确定。本文选取2012～2016年的发射活动作为演化计算中连续5年的航天器发射活动，每隔5年重复一次该发射规模。即发射模型是时间的周期性函数，周期为5年。新发射入轨的航天器在不同高度的分布情况，由2012～2016年的航天器发射分布情况确定。2012～2016年间年发射规模在表1中给出。

表1 2012～2016年间的航天器发射情况Table 1 The spacecraft launch traffic over 2012～2016

进行碎片环境长期演化计算中，需要对碎片的运动状态按照一定时间步长进行推演更新。由于空间碎片数量众多，且在长期演化过程中不断动态变化，对碎片的状态推演更新方法的效率和精度均提出了较高的要求。在演化计算模型中，通过对碎片的运动状态在一个轨道周期内求平均，分离出短周期运动部分，得到碎片运行的平均轨道。建立摄动力作用下，描述平均轨道变化率的运动方程。由于分离了短周期运动部分，可以采用较大的积分步长，如可将积分步长设置为1天，能够大大提高碎片运动状态的演化计算效率[8]。

最后，基于MPI(Massage Passage Interface)并行标准[27]，设计了大规模空间碎片演化的并行计算框架，能够高效利用“天河一号”等超级计算机平台的计算资源进行大碎片环境的长期演化。

2 模型求解

2.1 简化分层离散化模型的解析解

对分层离散化模型进行简化，忽略碎片之间的相互碰撞作用，分析在大气阻力作用下空间碎片环境的长期演化特点。将碰撞相关项从方程(8)中去除，整理可以得到仅有大气阻力作用下，碎片环境演化的约束方程：

(13)

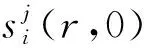
(14)

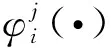
(15)

(16)

(17)

进一步求解方程(16)，得到简化分层离散化模型的通解为：

(18)

式中:变量α利用(17)来确定。

i=1,2,…,Nhj=1,2,…,Na

(19)

2.2 分层离散化模型的数值求解

当考虑空间目标之间的相互碰撞作用时，可通过求解方程(8)得到碎片环境的演化状态。将方程(8)改写成式(19)的形式。可以看出，考虑目标相互碰撞时的分层离散化模型由Nh×Na个高度耦合的一阶线性双曲型偏微分方程构成，可通过逼近双曲方程的差分格式进行数值求解。将改写成标准的双曲型形式为：

(20)

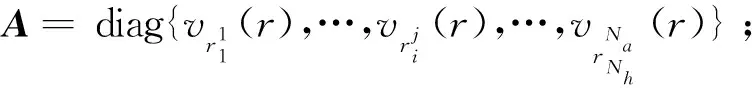
(21)

式中

(22)

式中:τ和h分别是差分逼近时的离散时间间隔和离散高度间隔，下标n表示第n个离散时间步长。容易证明，当满足条件约束条件(23)：

(23)

差分格式(21)可以对方程(19)实现稳定逼近。需要说明的是，为了确保约束控制方程(19)成立，在选择离散时间间隔和离散高度间隔时，应保证每一步计算时，同一高度层内的碎片最多衰减到下一个高度层内。

2.3 长期演化计算模型的蒙特卡罗仿真实现方法

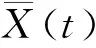
(24)

3 碎片环境的长期演化结果与分析

低地球轨道空间是当前目标分布最为密集的区域。本节以低地球轨道碎片环境为研究对象，利用分层离散化模型和长期演化计算模型，开展碎片环境长期演化分析。这里选取低地球轨道碎片环境的空间分布范围是距地面高度在200～3000 km的空间。仅考虑尺寸大于10 cm的空间碎片，并假设航天器在轨工作期间的轨道构型不发生变化，不进行碰撞规避机动。

演化计算中，空间目标的初始状态利用观测数据确定。根据空间监视网(SSN)的观测数据，截至到2016年9月，低地球轨道上运行着12000个编目目标。将低地球轨道空间，按10 km间隔划分为280个高度层；对于同一个高度层内的碎片，按照等对数间隔的原则将碎片划分到10个尺寸区间内，即要求各尺寸区间边界对数值的差值相等。根据1.1节中的分层离散化方案，在表2中，将低地球轨道上的空间碎片划分到2800个碎片组，并给出了每个碎片组的初始空间密度。

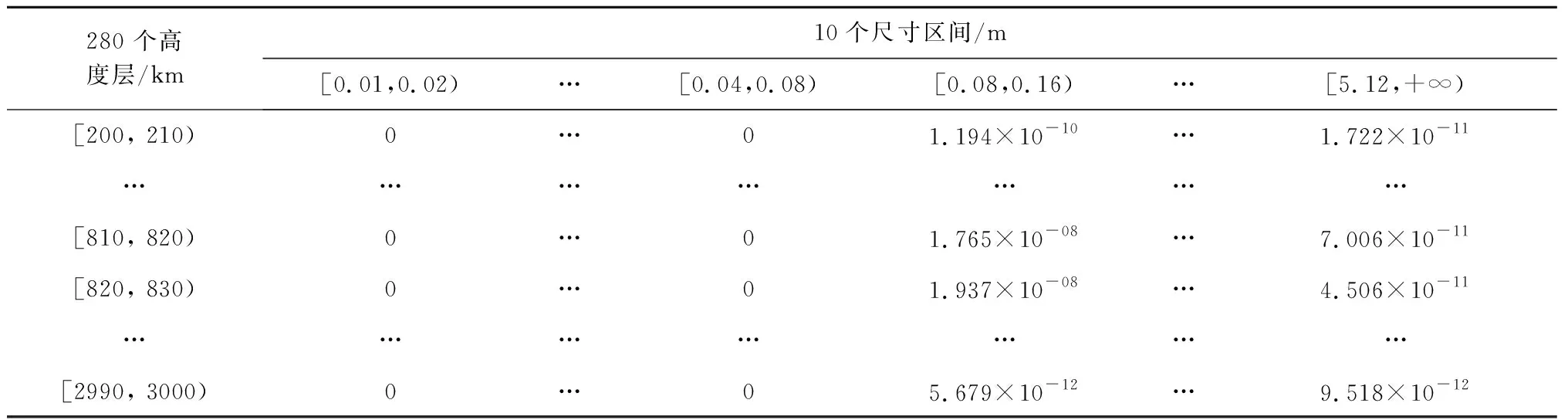
表2 编目目标的初始空间密度分布(1/km3)Table 2 Initial spatial density of the catalogued objects (1/km3)

3.1 摄动力作用下碎片环境的自我净化能力分析

仅考虑动力学约束，对碎片环境进行长期演化，可用来分析分层离散化模型和演化计算模型的力学条件是否一致，并讨论碎片环境的自我净化能力。

仅有摄动力的作用下，基于解析的分层离散化演化模型即方程来获取碎片环境的长期演化结果。碎片环境的初始状态si,j(r,0)在表2中给出。针对尺寸大于10 cm的碎片在未来200年内的演化增长趋势和分布状态分别如图4和图5所示。

从图4可以看出，仅有考虑摄动力的作用下，经过200年的演化，碎片的规模从从初始12000个减少到5800多个。进一步从图5可以看出，位于1000 km高度以下碎片的密度减少趋势较为明显，1000 km高度以上碎片的空间密度没有明显变化。

作为对比，利用长期演化计算模型，对低地球轨道碎片环境未来200年内的状态进行演化分析，如图6和图7所示的碎片环境演化结果。对比图4和图6、图5和图7可以看出，仅考虑摄动力作用下，利用两种模型计算得到的碎片数量的减少趋势、碎片在空间中的分布状态的变化都是一致的。综合两种模型的演化结果可以看出，碎片数量在未来200年内减少了约50%。这说明在摄动力的作用下空间碎片环境具有一定的自我净化能力，但这种自然清除过程是缓慢的。

两种模型均能给出碎片环境的长期演化结果，但两种模型所需要的计算量相差较大。表3给出了两种模型所需要计算量的统计，可以看出，长期演化计算模型需要的计算量大约是分层离散化模型所需计算量的104倍。

因此，分层离散化模型适合在计算资源有限的条件下，以较少的计算量，得到碎片规模的长期增长趋势，从整体上把握碎片环境的演化特点。长期演化计算模型中包含的摄动力因素较为全面，能够跟踪空间目标之间发生的每一次碰撞事件，适合在具有大量计算资源的条件下，对碎片环境的增长规模、空间分布状态进行精确、可靠的分析。

表3 仅考虑摄动力作用时两种演化模型的计算量统计Table 3 Compute assumptions of the two evolution models

3.2 考虑目标相互碰撞作用时碎片环境的稳定性分析

假设一种理想演化条件，即停止一切未来的航天发射活动，考虑碎片受到的作用力和空间目标之间的相互碰撞作用，分析当前碎片环境的稳定性。首先，定义碎片环境的两种长期演化状态：(1)稳定演化状态。处于稳定演化状态的空间碎片环境，空间碎片数量保持不变，甚至在不断减少。(2)不稳定的演化状态。当碎片环境处于不稳定演化状态时，空间碎片的数量在持续增加。

从理想条件下碎片数量的增长趋势看以看出，近地轨道上总碎片数量随演化时间在不断增加，200年内增加为初始碎片数量的近3倍，如图8所示。其次，从碎片的来源看，空间碎片中碰撞解体碎片所占的比例在逐年增加，演化结束时80%以上的碎片均为碰撞解体碎片。因此，即使停止一切航天发射活动，大量解体碎片仍将促使总的碎片数量持续增加，表明当前低地球轨道上的空间碎片处于不稳定演化状态。

图10给出了，从长期演化模型计算结果中，统计得到的目标累积灾难性碰撞次数随时间变化曲线。可以看出，在200年的演化时间内，目标之间发生了近30次灾难性碰撞，累积碰撞次数随演化年份呈现线性增长的趋势，这与LEGEND模型的演化结果是一致的[29]。

表4给出了理想演化条件下不同尺寸目标之间发生碰撞的次数。统计时若包络尺寸半径超过1 m，则目标为空间大尺寸目标，包络尺寸半径小于1 m的为小尺寸目标。可以看出，近三分之二的碰撞解体发生在大尺寸目标和小尺寸目标之间，大尺寸目标和小尺寸目标发生碰撞次数是大尺寸目标之间发生碰撞次数的3倍多。因此，大尺寸目标解体会产生大量解体碎片，解体碎片会进一步与大尺寸目标发生碰撞，产生更多的解体碎片，这种“碰撞—解体碎片—碰撞”反馈连锁碰撞效应，使得解体碎片数量迅速增加。

3.3 航天发射活动对碎片环境演化的长期影响

针对低地球轨道碎片环境，利用航天发射活动模型，分析发射活动对空间碎片环境的影响。通过对碎片环境的20次演化结果进行统计平均，得到200年的演化结果如图11和图12所示。考虑航天发射活动后，空间碎片数量急剧增加，在200年内尺寸大于10 cm碎片数量增加到约16万。碰撞解体碎片占总碎片比例也在逐年增加，至演化结束时刻，95%以上空间碎片是由目标碰撞解体产生的，如图11所示。

表4 理想演化条件下不同尺寸目标发生剧烈碰撞的次数Table 4 The catastrophic collision numbers between different size of space objects under the ideal condition

结合剧烈碰撞次数的统计结果，如图13和图14所示，可以看出，由于航天发射活动在不断向空间中引入大尺寸空间目标，“碰撞-解体碎片-碰撞”的反馈连锁碰撞效应加强，导致近地轨道上空间碰撞解体碎片数量迅速增加，这在[500, 800] km高度范围内表现尤为明显，如图14所示。

表5给出了不同尺寸目标之间发生剧烈碰撞的次数，与理想演化条件下的演化结果相比，大尺寸目标之间发生碰撞的次数、大尺寸目标与小尺寸目标发生碰撞的次数都明显增加了，进一步说明航天发射活动促进了碎片环境的连锁碰撞效应。

表5 考虑航天发射活动时不同尺寸目标发生碰撞的次数Table 5 The catastrophic collision numbers between different size of space objects with spacecraft launch traffic

4 结 论

随着空间碎片数量的不断增加，空间碎片在占据有限轨道资源的同时，也使在轨工作航天器面临着日益严峻的碰撞风险，空间碎片环境已严重影响了人类对空间资源的可持续开发利用。本文紧跟空间碎片环境研究这一热点问题，对空间碎片环境的长期演化建模问题进行了研究，建立了空间碎片环境的长期演化计算模型和分层离散化演化模型，并讨论了碎片环境的长期演化趋势和稳定性。结果表明，空间目标的相互碰撞解体，是空间碎片不断增加的主要因素；即使停止一切航天发射活动，空间碎片的数量仍在不断增加，表明低地球轨道空间碎片规模已经超越稳定临界点；如不采取有效的碎片减缓策略，未来航天发射活动会进一步增强空间碎片环境演化的不稳定性，加剧“碰撞-目标解体-碰撞”反馈连锁碰撞效应。论文的研究为掌握碎片环境的长期演化机理奠定了理论基础，提供了有效的分析工具；将为航天器的安全运行和空间资源的可持续开发利用提供重要支撑。