采用观测器的偏置动量小卫星姿态容错控制
袁斌文,尤 政,孟子阳,杨 登
(1. 清华大学精密仪器系,北京 100084;2. 中国卫星海上测控部,江阴 214431)
0 引 言
近年来,容错控制方法被广泛应用于无人机、卫星等领域[1-2]。容错控制[3]是指在故障发生的情况下,通过设计控制器使系统能够自动补偿部件故障的影响,维持系统的稳定性,尽可能地将系统的工作性能恢复至故障前的水平,保证系统可靠运行。小卫星由于受质量、尺寸、能耗等的限制,具有控制机构单一、防护措施简单、冗余配置少、星上资源有限等特点,这就使得对小卫星进行容错控制非常必要。尤其对于小卫星的姿控系统,其工作可靠性、稳定性决定了小卫星能否正常完成各项飞行任务,直接影响着小卫星的工作性能和在轨寿命。因此,对小卫星姿态容错控制策略进行研究,对于提高姿控系统在轨运行的可靠性和稳定性、提高小卫星在轨自主运行能力有着重大的理论和现实意义。
近年来,航天领域中,已开展了很多关于飞行器姿态容错控制的研究[2]。2006年,Tafazoli等[4]采用反馈线性化策略设计容错控制器,实现了挠性航天器在执行器故障、外界干扰力矩等情况下的姿态自主恢复。2010年Baldi等[5]考虑在轨航天器执行机构失效故障,采用非线性几何方法进行干扰解耦,通过获得的故障信息自主调整控制器参数,保证航天器姿态稳定控制。2011年,李波等[6]针对采用四反作用轮的过驱动航天器,基于自适应滑模控制方法和动态控制分配算法设计容错控制器,有效提高了系统可靠性。2013年Li等[7]考虑航天器机动中可能出现的轨道不确定性和推进器故障,基于李亚普诺夫稳定性理论和遗传算法,通过求解线性矩阵不等式设计了容错控制器。2014年肖冰[8]基于非线性观测器技术设计可重构控制方法保证配备冗余执行器的航天器具有自主姿态容错控制性能。2016年,李冬柏等[9]针对未知飞轮摩擦力矩和环境干扰力矩下的姿态跟踪问题,提出了一种鲁棒自适应姿态控制律。2017年,陈嘉文等[10]针对任务约束条件下航天器姿控系统在轨故障重构问题,提出一种基于自适应动态规划的重构优化决策算法。总的来说,在航天器姿态容错控制领域,国内外学者已经开展了较为系统性的研究,运用不同的观测、控制理论对外部干扰、不确定参数、执行器故障等进行容错控制。然而,其中大多数方法对姿控系统执行器运行状态数据依赖性强,且仅适用于三/四反作用轮姿控系统,对广泛应用于小卫星的偏置动量姿控系统的容错控制研究还比较少。
偏置动量姿控系统采用三轴磁力矩器和俯仰轴偏置动量轮作为执行机构,具有造价低、结构简单、能量消耗少、适应性强等优点,因而被广泛应用于小卫星系统。本文立足于工程应用实际,针对偏置动量姿控系统中客观存在的执行器故障、外部干扰力矩等不确定项,提出一种基于不确定项观测器的容错控制方法,在此基础上,运用Lyapunov稳定性原理分别对观测器、控制器的收敛性进行了分析,并通过数值仿真校验该方法的有效性,仿真结果表明,该方法能够实现对执行器故障、外部干扰力矩等不确定项的容错控制。
1 偏置动量姿控系统数学模型及控制流程
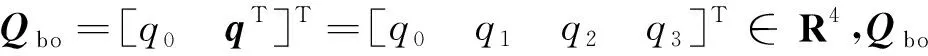
(1)
此即卫星的运动学方程,其中,H(Qbo)为正交矩阵,满足H(Qbo)HT(Qbo)=I4:
(2)
设I为卫星转动惯量矩阵,对于质心惯性主轴坐标系ObXbYbZb,有
I=diag(Ix,Iy,Iz)
(3)
式中:Ix,Iy,Iz分别为卫星绕x,y,z转动的转动惯量。同时,设卫星相对于惯性坐标系的角速率为ωbi,h为动量轮相对于卫星平台的角动量矢量,TMT为磁力矩器输出的控制力矩,d为作用于卫星的外部干扰力矩的总和,则卫星的角动量定理可写为[11]
(4)
(5)
对于安装在俯仰轴上的动量轮,设l为动量轮的转轴方向单位矢量,TMW为动量轮由于相对转速变化而产生的对卫星的反作用力矩,则对该轮,有下式成立
(6)
结合式(4)和式(6),可得卫星动力学方程如下:
(7)
式中:Tact=TMT+lTMW,表示执行器的总控制力矩。
采用俯仰轴偏置动量控制方式的小卫星在星箭分离后或长时间不进行姿态控制时,需要采用Y-Thomson初态控制方法[12],依次经过角速率阻尼、俯仰轴起旋、姿态过渡等控制阶段,才能最终进入三轴稳定状态。角速度阻尼阶段将小卫星滚动、偏航轴方向的角速率阻尼至零附近,为进入俯仰轴起旋阶段作好准备。俯仰轴起旋阶段在继续对滚动轴、偏航轴角速率进行阻尼的同时,使小卫星俯仰轴起旋并将其角速率稳定在某一预定值ωy-ref(ωy-ref<0)附近,该预定角速率可通过下式得出
(8)
式中:J为动量轮转动惯量,ΩMW为动量轮额定转速。该阶段使星体俯仰轴起旋的目的有两个:一是使星体俯仰轴进动到与轨道面垂直的位置[13];二是储存一定的角动量以便于在下一阶段与动量轮进行角动量交换。姿态过渡阶段动量轮启动,其转速保持在额定转速附近,通过磁力矩器阻尼使三轴角速率保持在零附近。完成姿态过渡阶段后,小卫星进入对地定向三轴稳定模式,这也是小卫星的长期工作模式。三轴稳定控制阶段由动量轮控制俯仰轴的姿态,由磁力矩器完成滚动轴、偏航轴的姿态控制并对动量轮进行加/卸载,将动量轮转速稳定在额定转速附近,防止其因转速饱和而失去控制能力。
2 基于不确定项观测器的滑模容错控制方法
2.1 容错控制方法总体设计
俯仰轴动量偏置姿控系统的初始控制阶段大多在地面站控制下完成,对执行机构容错要求较低,因此,本文主要对三轴稳定状态下的执行机构容错控制进行讨论。
(9)
(10)
将式(9)、式(10)代入卫星动力学方程即式(7)中,可得
(11)
(12)
将式(12)代入式(11)中,可得
(13)
(14)
当执行器出现故障时,其实际输出力矩看成是由两部分组成,一部分为控制指令对应的理想情况下的执行器输出力矩即标称控制力矩Tc,另一部分为输出力矩偏差Terror。因此有:
(15)
对式(1)的两边求导,可得
(16)
将式(15)代入式(16)
(17)
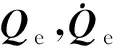
(18)
则式(17)可进一步改写为
(19)
式中:
(20)
针对姿控系统中客观存在的不确定项,为了实现小卫星姿态稳定控制,参考文献[8]中所提出的针对三轴反作用轮姿控系统的故障重构方法,本文将引入一种基于不确定项观测器的滑模容错控制方法,其控制流程如图1所示。图1中,不确定项观测器用于对Tuncert进行估计,姿态控制量包含常规控制项与补偿控制项两部分,常规控制项由滑模控制器计算得到,补偿控制项根据不确定项观测器得出的Tuncert的估计值进行设计,用于补偿执行器故障等对姿控系统的影响。此时姿态控制器可表示为:
Tc=Tc_nor+Tc_comp
(21)
2.2 不确定项观测器设计
针对式(19)中所表示的二阶非线性系统,本文借鉴一种适用于欧拉-拉格朗日系统的非线性观测器[14-15]对姿控系统中的不确定项进行估计。该观测器适用于形如式(19)的欧拉-拉格朗日系统,但要求M(Qbo)为对称正定矩阵。对于本文的姿控系统,虽然M(Qbo)不是对称正定矩阵,然而M-1(Qbo)主对角线两侧对称的项反号,因此可通过Lyapunov稳定性原理证明该非线性观测器依然适用于本文的姿控系统。设计不确定项观测器如式(22)所示。
(22)
(23)
式中:λ为大于零的控制参数。
(24)
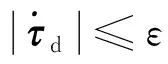
(25)
进一步有式(24)的后两项之和为零,消去后两项得
(26)


(27)
一般来说,在小卫星姿态受控的情况下均能保证q0≠0。
(28)
2.3 滑模控制器设计
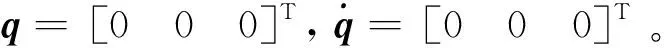
(29)
(30)
根据二阶非线性系统滑模控制方法,选取如下滑模面[8]:
(31)
式中:α,β,γ为控制参数,γ>0,α,β为正奇数且满足1<α/β<2;同时对任意向量x∈Rn,定义xα/β为
(32)
设计滑模控制器的控制律如下:
(33)
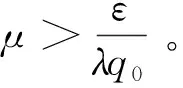
(34)
记
(35)
则有
(36)
在小卫星姿态受控的情况下,近似有q0≈1,因此根据式(36)可进一步得到系统常规控制项表达式
(37)
综上可知,基于不确定项观测器的容错控制器最终输出的控制力矩为
(38)

证. 选取Lyapunov候选函数V2(t)=0.5sTs,可得V2(t)对时间的一阶导数
(39)
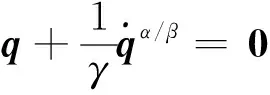
值得注意的是,由于函数sgn[s(t)]不连续,因此应用式(38)进行控制时,容易出现滑模控制中普遍存在的抖振问题,为削弱此抖振,在实际的实施过程中,应用连续函数s(t)/(|s(t)|+σ)代替非连续函数sgn[s(t)],此时控制律变为
(40)
3 仿真结果分析
为了校验本文所提出的基于不确定项观测器的滑模容错控制方法在执行器容错、抗环境干扰方面的有效性,利用MATLAB/Simulink软件,对该算法的容错控制性能进行数值仿真分析。同时,为体现本文所提容错控制方法的控制效果,选用广泛使用的PD控制器与之进行对比。仿真参数以某型在轨小卫星的实际设计参数和轨道参数为依据,详细参数如表1所示。
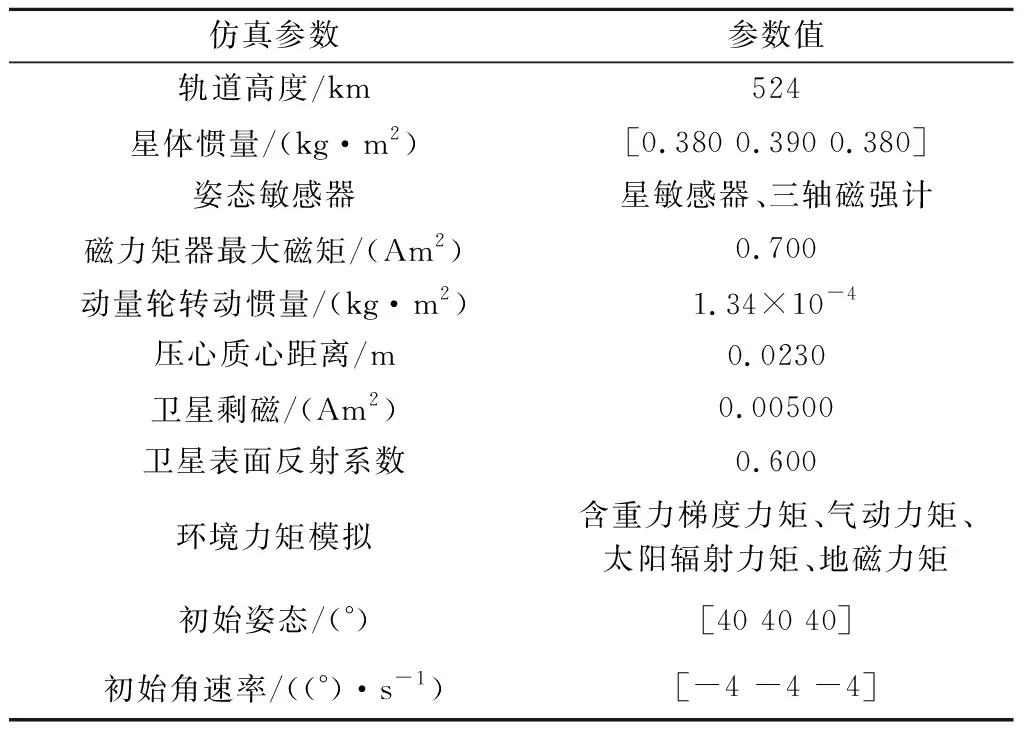
表1 小卫星姿控系统数值仿真参数Table 1 Numerical simulation parameters
仿真过程中的不确定项观测器参数、滑模控制器参数及对比所用的PD控制器参数见表2。

表2 仿真控制器参数Table 2 Simulation controller parameters
仿真时选用转动惯量为J=1.34×10-4kgm2的动量轮,动量轮额定转速设定为ΩMW=1500 r/min,转速控制精度为3 r/min (3σ)。利用磁力矩器对动量轮进行加/卸载,卸载力矩为
Tload=η(Ω-ΩMW)
(41)
式中:Ω为飞轮当前转速,η为控制系数,仿真中取η=4×10-8。
设磁力矩器的命令控制力矩为Tc,T,动量轮的指令控制力矩为Tc,W。仿真时:
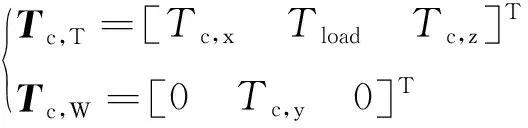
(42)
3.1 环境力矩作用下仿真结果
针对小卫星在轨运行过程中客观存在的环境力矩,为校验本文所提容错控制算法的性能,将小卫星所受干扰力矩调整为正常干扰力矩的4倍并进行仿真。图2为小卫星实际所受环境干扰力矩与不确定项观测器估计值的对比图,其中俯仰轴观测器估计值除环境干扰力矩外,还包含动量轮转速控制误差部分。两种控制方案下的姿态误差和角速度误差曲线分别如图3、图4所示。从仿真曲线可以看出,相比于PD控制器:
1)容错控制器能够显著提高俯仰轴姿态控制精度,但对滚动轴和偏航轴控制精度提高效果稍差。这主要是因为滚动轴和偏航轴的姿态依靠磁力矩器控制,而磁力矩器仅能产生垂直于当地磁场方向的力矩,欠驱动影响了容错控制效果。
2)如表3所示,由于滑模控制的“抖振”现象,使得容错控制器下的角速率控制误差大于PD控制。容错控制方式下,俯仰轴角速率标准差较大,约为1.50×10-3(°)/s。

表3 三轴角速率控制误差对比Table 3 Three axes angular rates errors comparison
3.2 动量轮性能故障仿真结果
在动量轮运行过程中,驱动电机老化、轴承润滑变差、轴承保持架不稳定等因素,均有可能致使动量轮输出力矩异常。假定动量轮发生式(43)所表示的性能故障[8],其中,Tin(t)为动量轮指令对应力矩,Tout(t)为动量轮实际输出力矩,δ(t)为随机噪声。
Tout(t)=0.7Tin(t)+7×10-6sin(0.01t)+δ(t)
(43)
在同时存在环境力矩和动量轮性能故障的情况下进行仿真。仿真结果中,滚动轴和偏航轴姿态受动量轮性能故障影响较小,仿真曲线与环境力矩情况下相似,此处省略,两种控制方案下俯仰轴的姿态角误差和角速率误差曲线如图5所示。
结合环境力矩、动量轮性能故障两种条件下的仿真结果可以看出,本文提出的基于不确定项观测器的姿态容错控制方法具有良好的观测性能和优越的控制性能,能够实现对执行器故障、小卫星外部扰动力矩的容错控制。
4 结 论
针对偏置动量姿控系统,提出一种基于不确定项观测器的滑模容错控制方法。设计了不确定项观测器对执行器故障、小卫星外部扰动力矩等不确定项进行估计,理论证明该观测器的观测误差一致最终有界(UUB)。容错控制器在非奇异终端滑模控制器的基础上,结合不确定项观测器进行反馈补偿,进而实现小卫星姿态容错控制。稳定性分析表明,该方法能够快速收敛到滑模面并进一步实现三轴稳定控制。仿真实例表明该容错控制方法具有可行性,且具有实际应用价值。

