分块变换和GPU并行的遥感影像快速正射校正方法

方留杨 何红艳 张炳先



分块变换和GPU并行的遥感影像快速正射校正方法

方留杨1何红艳2,3张炳先2

（1 云南省交通规划设计研究院有限公司 陆地交通气象灾害防治技术国家工程实验室，昆明 650041）（2 北京空间机电研究所，北京 100094）（3 先进光学遥感技术北京市重点实验室，北京 100094）

正射校正是整个遥感数据处理过程中计算量最大、耗时最长的步骤之一，已经成为制约整个遥感数据处理快速完成的瓶颈。为了提高正射校正处理效率，文章系统地探讨了基于分块三维直接线性变换和图形处理单元（GPU）并行的遥感影像快速正射校正方法。首先针对正射校正坐标转换计算量过大的问题，提出了分块三维直接线性变换策略，有效地降低了坐标转换的计算量；在此基础上，采用“渐进式”策略开展GPU并行处理，首先通过GPU并行映射（核函数任务映射、基本设置），使方法在GPU上可执行，然后通过“两层次”性能优化（核函数性能优化、整体流程性能优化），进一步提高了方法的执行效率。在CPU和GPU组成的实验环境中，使用文中方法对“高分二号”卫星全色标准景影像进行实验，GPU执行时间仅为5.13s，与CPU相比，相应加速比达到142.42倍，可以满足对大数据遥感影像的快速正射校正需求。

正射校正 分块三维直接线性变换 图形处理单元并行映射 核函数性能优化 整体流程性能优化 遥感数据处理

0 引言

正射校正是遥感影像数据处理的关键环节，也是整个遥感数据处理过程中计算量最大、耗时最长的步骤之一。对大数据遥感影像的处理时间过长，已成为制约整个遥感数据快速处理的瓶颈，给遥感影像在灾害防治和救援、应急抢险等高时效行业领域的应用带来了巨大挑战[1-3]。近年来，以图形处理单元（Graphics Processing Unit，GPU）为代表的通用计算硬件逐渐成为国际上解决大数据计算和实时处理问题的主流方案，GPU专门为计算密集型、高度并行化的处理任务设计，为许多对计算速度有很高要求的问题提供了全新的解决方案[4]，其中在正射校正方面开展的研究和应用主要包括：2009年，Pro-Lines GeoImaging server软件（由PCI Geomatics公司研发）的正射校正模块引入了GPU并行处理技术，有效提高了其处理效率[5]，文献[6]基于GPU顶点图形渲染和纹理映射技术实现了航空影像正射校正，但该方法并未涉及GPU通用计算技术。在国内，文献[7]对遥感影像GPU正射校正的效率和正确性进行了验证，说明了该技术的可行性；文献[8]提出了基于GPU的高光谱影像几何校正模型，但未对实现方法进行详细阐述；文献[5]探讨了GPU/CPU协同的遥感影像正射纠正方法，但受实验环境等客观条件限制，并未对性能优化方法进行深入分析；文献[9]和文献[10]先后提出了星载高分辨率SAR影像的GPU几何校正方法；文献[3]使用“层次性分块”策略设计了基于CPU和GPU协同处理的正射校正方法，但上述方法仅将算法简单移植至GPU上进行处理，并未进行充分的算法简化和性能优化，尚有较大的提升和完善空间。

本文首先针对传统正射校正方法中逐像素坐标转换计算量过大的问题，提出了一种分块三维直接线性变换策略，以有效减少坐标转换的计算量。在此基础上，从GPU并行映射（核函数任务映射、基本设置）、性能优化（核函数性能优化、整体流程性能优化）两个方面出发，探讨了使用GPU并行技术进行快速正射校正的方法。

1 快速正射校正方法

1.1 分块三维直接线性变换

遥感影像正射校正分为直接法和间接法两种方案[11]，其中间接法方案基于输出影像（即校正后影像）进行任务划分，根据坐标投影转换关系、有理多项式（RPC）模型和数字高程模型（DEM），逐像素建立输出影像物方空间坐标与输入影像（即待校正影像）像方坐标的转换关系，然后对输入影像进行重采样。该方案的并行程度较高，可以直接获取输出影像上每个像素的灰度值（不涉及输出影像灰度值再分配），适合于在GPU进行并行处理，但其坐标转换和重采样的计算量都很大。为了有效降低坐标转换的计算量，本文提出一种分块三维直接线性变换策略（如图1所示）：即对输出影像进行格网划分，仅在格网顶点处严格按照坐标投影转换关系、RPC模型和DEM求解输出影像和输入影像像点的坐标对应关系，格网内各像点坐标则通过近似的简化模型建立联系。由于描述的是输出影像三维空间坐标和输入影像二维像点坐标之间的关系，因此选择三维直接线性变换模型作为简化模型，即

式中s和l为输入影像二维像点坐标；x、y、h为输出影像三维空间坐标；a0~a6、b0~b6为三维直接线性变换模型参数。

三维直接线性变换模型包含14个参数，需至少列出14个方程才可求解，但每个格网同名顶点仅可列2个方程，4个格网同名顶点合计只能列8个方程，无法求解。为增加方程数，本文引入虚拟格网同名点的概念，即首先根据坐标投影转换关系、RPC模型和DEM计算得到4个真实格网同名顶点坐标，再将DEM中真实高程分别增加和减少一个常数，保持坐标投影转换关系和RPC模型不变，求解得到8个虚拟格网同名点坐标，这样格网同名点数量从4个增加至12个，能列出24个方程，可以通过最小二乘法求解出14个参数，求解思路如图2所示。

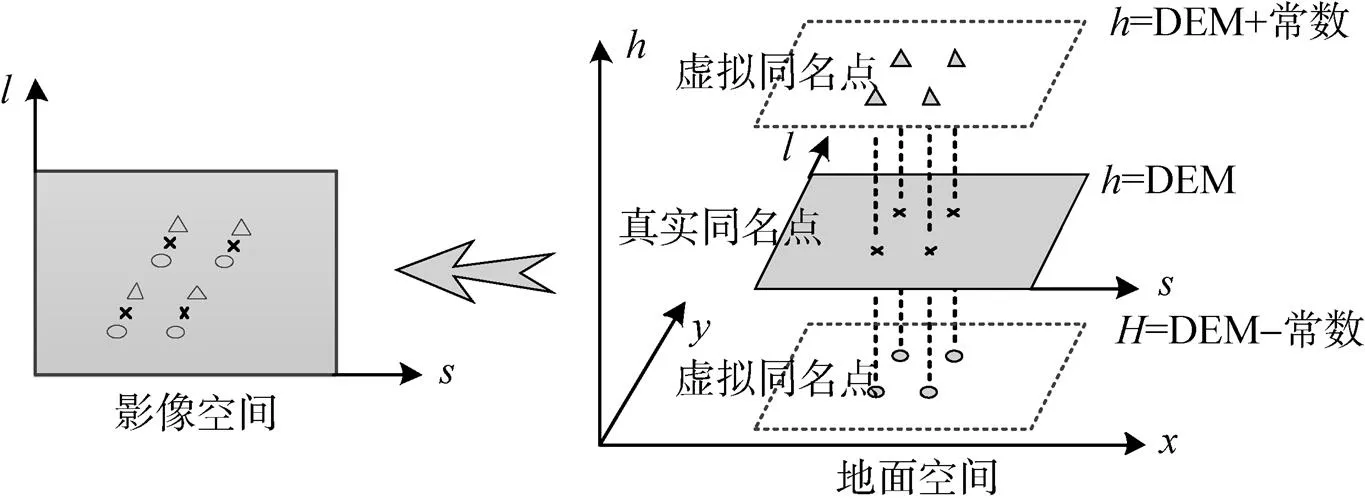
图2 引入虚拟格网同名点计算三维直接线性变换模型参数

1.2 GPU并行处理

引入分块三维直接线性变换后，虽然有效降低了坐标转换的计算量，但却额外引入了变换模型参数拟合的计算量，并且重采样的计算量并未减少，因此整个正射校正的计算量仍然很大，需要使用GPU并行处理技术，进一步提高方法的执行效率。本文选择目前主流的统一设备计算架构（CUDA）作为GPU并行处理框架[12]，采用“渐进式”策略开展GPU并行处理：首先通过GPU并行映射，明确核函数执行流程和基本设置，确保方法在GPU上可执行；然后通过“两层次”性能优化，进一步提高方法在GPU上的执行效率。

1.2.1 GPU并行映射

（1） 核函数任务映射

首先进行核函数任务映射，以确定GPU上正射校正执行的逻辑流程。由于格网同名点坐标转换计算、三维直接线性变换模型参数计算、影像重采样计算都具有逐格网/像素独立的特点，具有很高的并行性，因此，基于最大限度的GPU端并行执行原则[13]，将上述3个步骤都映射至GPU执行。考虑到3个步骤的逻辑连续，为减少反复调用核函数带来的额外开销，进一步将3个步骤分别映射为3个独立的核函数GC_CorPtsCal、GC_Dlt3DCal、GC_Resample实现，映射关系如图3所示。

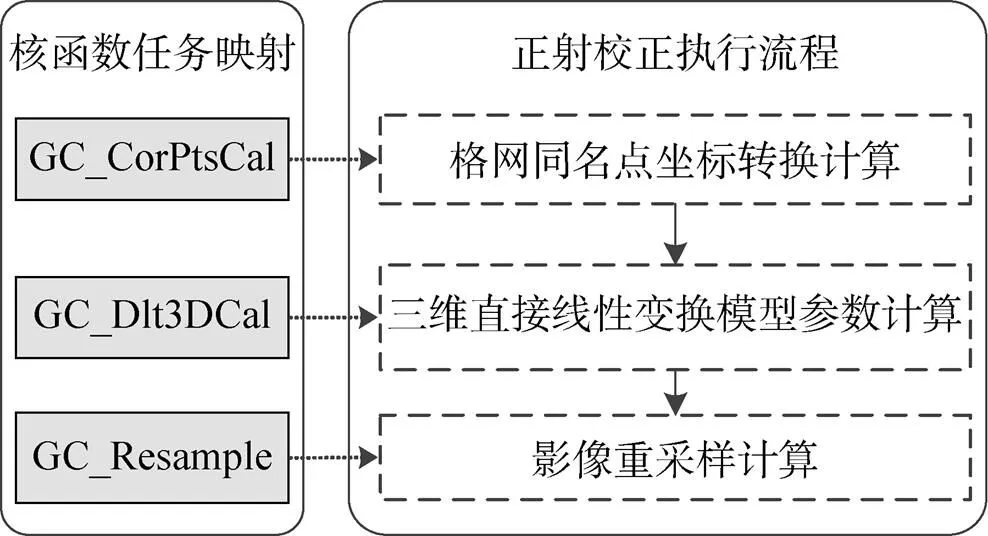
图3 正射校正核函数任务映射

（2） 基本设置

进行核函数任务映射后，接下来需要进行基本设置，使算法在GPU上可执行，具体包括：

1）将每个CUDA线程设置为仅对一个元素进行计算。具体来说，对于GC_CorPtsCal核函数，每个CUDA线程负责一个格网同名点坐标转换的计算；对于GC_Dlt3DCal核函数，每个CUDA线程负责一组格网三维直接线性变换模型参数的计算；对于GC_Resample核函数，每个CUDA线程负责对一个像素进行重采样。

2）将核函数线程块大小设置为256像素（16像素×16像素）。

3）为减少对全局存储器的多次访问，使用程序默认的L1 cache缓存模式。

4）为减少使用循环指令带来的开销，使用程序默认的循环展开模式。

5）坐标投影转换参数和RPC模型参数较少且为常数值，满足常数存储器的存储容量和对数据只读的要求，因此将其载入常数存储器中，以提高参数的访问效率。

1.2.2 GPU性能优化

GPU性能优化分为两个层次进行：核函数性能优化和整体流程性能优化。首先对3个核函数进行性能优化，以提高核函数的执行效率；然后进行整体流程性能优化，通过传输计算堆叠隐藏CPU和GPU的数据传输开销，以进一步提高方法的整体执行效率。

（1） 核函数性能优化

对核函数进行性能优化的方法包括：线程多元素重访、线程块大小和形状最优选取、存储层次性访问[14]。

线程多元素重访基于GPU网格和线程寻址指令可以多次使用以及存储访问流水化的特性，同时分配多个元素（格网或像素）处理任务给单个GPU线程处理，以提高任务的整体处理效率[14]，但线程多元素重访的效率受数据划分模式、负载大小等因素的影响，对不同核函数的性能提升程度并不相同，因此需通过实验分别确定3个核函数GC_CorPtsCal、GC_Dlt3DCalGC_Resample中各线程处理元素的具体数量，使算法执行效率达到最优。此外，随着线程处理元素数量的不断增长，若待处理数据不变，在线程块大小固定的情况下，线程块的数量将会逐渐减少，在该种情况下，需要保证给每个流式多处理器中至少分配1个线程块，以充分利用GPU的计算性能。

线程块大小选取时需考虑以下因素：1）线程块的大小应至少在64线程以上；2）线程块最大不能超过1 024线程；3）线程块的大小应该是线程束数量（32线程）的整数倍，以避免在未完全展开的线程束上进行无意义的操作。此外，由于线程块的宽度会影响全局存储器的合并访问效率，并且GC_CorPtsCalGC_Dlt3DCalGC_Resample三个核函数的全局存储器访问模式各不相同，因此将各线程块的宽度从1线程增加到最大，并记录3个核函数的执行时间，以寻找核函数执行时间最短时对应的线程块宽度。

存储层次性访问利用GPU的多级缓存提高方法的访存效率。通用计算GPU提供了两级缓存，在基本设置中，核函数采用了默认的一级缓存（L1 cache）进行数据缓存，但二级缓存（L2 cache）同样可进行数据缓存。此外，GC_Resample核函数进行影像重采样时的数据内插具有明显的二维局部性访存特点，该特点适合于使用纹理存储器进行优化。因此在实验部分，分别记录核函数GC_CorPtsCal、GC_Dlt3DCal采用L1 cache、L2 cache时的执行时间，以及核函数GC_Resample采用L1 cache、L2 cache、纹理存储器时的执行时间，确保将核函数性能调至最优。

（2） 整体流程性能优化

通用计算GPU内部固化有一个数据拷贝引擎和一个核函数执行引擎[15]，而基于分块变换的GPU正射校正也包含1次内存至显存的数据拷贝操作、3次核函数执行操作（GC_CorPtsCal、GC_Dlt3DCal、GC_Resample）和1次显存至内存的数据拷贝操作。因此可使用流处理机制，将2次数据拷贝操作（内存至显存，显存至内存）分配给数据拷贝引擎，将3次核函数执行操作分配给核函数执行引擎，并指定多组流操作，同时进行多组数据拷贝和核函数执行，以提高两个引擎的使用效率。但由于对大数据量遥感影像进行处理时，有时受GPU显存容量的限制，需要进行多轮数据拷贝操作，如果在数据拷贝过程中出现数据叠掩和重复拷贝现象，会降低流的整体执行效率，因此需要通过具体实验确定流的数量，使GPU上正射校正的执行效率达到最优。

综上所述，分块变换和GPU并行的遥感影像快速正射校正方法流程如图4所示。

图4 分块变换和GPU并行的快速正射校正流程

2 实验结果与分析

2.1 实验数据及平台

2014年8月19日，我国在太原卫星发射中心成功发射“高分二号”卫星，该卫星搭载了2台分辨率为0.8m的全色相机和1台分辨率为3.2m的多光谱相机，可提供多种产品和应用服务，是迄今为止中国研制的空间分辨率最高的民用低轨遥感卫星[16]。其中全色相机标准景影像大小为29 200像素×27 600像素，采用10bit量化，数据量较大（约1.5 Gbyte），具有明显代表性，因此本节选择该影像作为实验数据。

本文实验平台的CPU为Intel Xeon E5650，主频2.66 GHz，含6个处理核心；GPU为NVIDIA Tesla C2050，含448个处理核心，显存容量为3 Gbyte，内部含有一个数据拷贝引擎和一个核函数执行引擎；主机内存为32 Gbyte。

2.2 方法性能

为定量评价算法性能，本节定义加速比评价加速后算法与加速前算法相比的速度提升程度，计算公式为

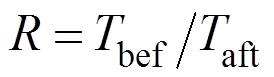
式中bef为加速前算法的执行时间；aft为加速后算法的执行时间；为加速比。加速比越高，说明算法的执行效率越优。

进行正射校正时需要同时为输入影像和输出影像分配GPU显存空间，但由于实验影像数据量太大，无法一次性全部载入，因此需要分块处理。本文按照行优先原则进行分块，将每次处理影像块的宽度固定为整幅输出影像的宽度，每次处理影像块的高度则按照式（3）计算：

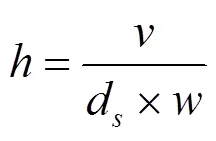
式中为算法分配给输出影像的内存空间，此处为512 Mbyte；d为影像数据类型需要占用的字节数，全色影像为10bit量化，因此其值为2；为输出影像宽度，其值为34 100像素。

将式（3）各项数值代入计算，得到每次处理的输出影像高度为7 872像素。由于整幅输出影像的高度为35 000像素，因此为了对整幅输出影像进行处理，正射校正需分为5次进行。此外，对算法作如下约定：输出影像坐标系为UTM投影坐标系，因此坐标转换通过UTM投影和RPC模型进行；格网大小为64像素×64像素；重采样方式为双线性内插。另外，为了专注于对方法本身效率进行讨论和分析，本节不涉及磁盘上数据的读/写（I/O）时间，仅讨论方法本身的执行时间（包括各步骤计算时间，以及CPU和GPU间的数据传输时间）。

首先，在Intel Xeon E5650 CPU上，记录对“高分二号”卫星全色标准景影像进行传统逐点坐标转换正射校正和分块三维直接线性变换正射校正的执行时间，结果如表1所示。由于UTM投影转换的计算量很大，因此逐点坐标转换正射校正中同名点坐标转换计算的耗时很长（471.06s），占整个校正时间（730.61s）的64.5%；进行分块三维直接线性变换优化后，虽然额外引入了三维直接线性变换模型参数计算的时间（53.41s），且重采样的计算时间相同（出现微小区别的原因在于程序执行时硬件性能的微小波动和计时误差），但由于同名点坐标转换计算时间（1.38s）大幅减少，因此整体上正射校正的执行时间（314.24s）仍显著缩短，相应加速比达到2.33倍。

表1 两种正射校正方法CPU逐步骤执行时间和加速比

Tab.1 CPU step-by-step run times and speedup ratios of two ortho-rectification methods

然后，通过GPU并行处理，进一步提高分块三维直接线性变换正射校正的执行效率。表2列出了GPU并行映射后正射校正各个步骤的执行时间，包括CPU→GPU数据传输时间、核函数执行时间、GPU→CPU数据传输时间以及其余项耗时（包括了显存分配、核函数启动、计时开销等操作的时间开销）。可以发现，进行了GPU并行映射后，正射校正处理效率得到了显著提升，3个核函数的加速比均达到了100倍以上，但由于额外增加了CPU和GPU之间双向数据传输和其余耗时项的执行时间开销，因此整体加速比为55.91倍，相应的执行时间5.62s。此外，对数据传输时间进行分析，发现CPU→GPU数据传输时间（1.07s）长于GPU→CPU数据传输时间（0.67s），这是由于卫星特有的成像特点使得正射校正算法在对某一输出影像块进行重采样时，需要的输入影像块范围比输出影像块大。由于该现象的存在，导致正射校正多次分块进行时，各输出影像块对应的输入影像块出现重叠，从而使得CPU→GPU数据传输量（3.58 Gbyte）大于GPU→CPU数据传输量（2.22 Gbyte），进而造成CPU→GPU数据传输时间长于GPU→CPU数据传输时间。

表2 GPU并行映射后方法各步骤执行时间和加速比

Tab.2 Run times and speedup ratios of ortho-rectification after GPU parallel mapping

采用1.2.2节中设计的性能优化策略对上述核函数进行性能优化。首先使用线程多元素重访策略，令一个CUDA线程处理多个元素，相应的核函数执行时间如图5所示。从图5中可知，对于3个核函数GC_CorPtsCal、GC_Dlt3DCal、GC_Resample，当每个CUDA线程分别处理8、16、128个元素时，核函数执行时间取得最小值，分别为9.8ms、366.2ms、1 331.6ms。进一步发现，GC_Resample的执行时间变化较为平稳，而GC_CorPtsCal、GC_Dlt3DCal的执行时间在每个CUDA线程处理16个元素后开始显著增加，造成该现象的原因是：在开始实验时，已确定分块格网大小为64像素×64像素，且线程块初始大小设定为16线程×16线程，因此当每个CUDA线程负责计算4×4个（即16个）格网点坐标和三维直接线性变换模型参数时，每个线程块的覆盖范围即可达到4 096像素×4 096像素，要覆盖每次处理的影像块（34 100像素×7 872像素），仅需9×2个线程块即可；NVIDIA Tesla C2050 GPU共有14个流式多处理器，要充分发挥其计算性能，需要至少给每个流式多处理器分配1个线程块，此时恰好可以满足要求，若再将每个CUDA线程处理的元素量增加，线程块数量会更少，已无法保证给每个流式多处理器分配一个线程块，在这种情况下，GPU的硬件计算资源没有得到充分利用，因此核函数的执行效率明显下降，对应的执行时间显著增加。

接下来讨论使用不同大小、形状和缓存模式的线程块时，3个核函数执行时间的变化情况，其中核函数GC_CorPtsCal的实验结果绘制于图6（a），核函数GC_Dlt3DCal、GC_Resample的实验结果绘制于图6（b）。柱状子图记录核函数执行时间（该执行时间为线程块宽度从1增加到最大时的最短执行时间），折线子图记录对应的线程块宽度。观察图6中所示的柱状子图及折线子图可以发现：

1）改变线程块大小对核函数GC_CorPtsCal、GC_Resample的执行时间无明显影响。这是因为这两个核函数涉及的坐标转换和重采样的计算逻辑较为复杂，其计算指令远多于访存指令（将RPC模型载入常数存储器后，GC_CorPtsCal甚至不需要访存），计算访存比高。因此，在线程块逐渐增大过程中线程占有率最低时，流式多处理器中驻留的线程束的数量也足够隐藏访问延迟[17]。此外，发现当线程块小于384线程时，改变线程块大小对GC_Dlt3DCal的执行时间无明显影响，原因同上；但当线程块大于384线程时，GC_Dlt3DCal的执行时间明显上升，这是因为当线程块大于384线程时，线程块数量已减少至无法保证给每个流式多处理器分配一个线程块，导致GPU的硬件计算资源没有得到充分利用，因此核函数的执行效率明显下降。

2）采用不同的缓存模式时，3个核函数的执行时间无明显差别。虽然核函数GC_Resample中存在着明显的二维局部访存模式，且该访存模式非常适合于使用纹理存储器进行加速，但在性能上纹理存储器并未体现出对于L1/L2 cache的优势。

3）当核函数执行时间取得最小值时，GC_Dlt3DCal和GC_Resample的线程块宽度总体上小于GC_CorPtsCal的线程块宽度，这是因为GC_Dlt3DCal和GC_Resample的访存模式较为复杂，其中GC_Dlt3DCal访问的是存储控制点坐标的结构体，因此每个线程访问的显存地址并不相邻，而是间隔了结构体大小的地址范围；GC_Resample的访存无固定模式，由于重采样反算的不规则性，不同行的输出影像反算到输入影像后有可能对应同一行，使得显存访问被合并，因此GC_Dlt3DCal和GC_Resample的执行时间在线程块宽度较小时即可取到最优值。GC_CorPtsCal不存在显存访问操作，因此核函数执行时间基本不受线程块宽度增加的影响，此处其执行时间在线程块宽度相对较大时取到最优值。

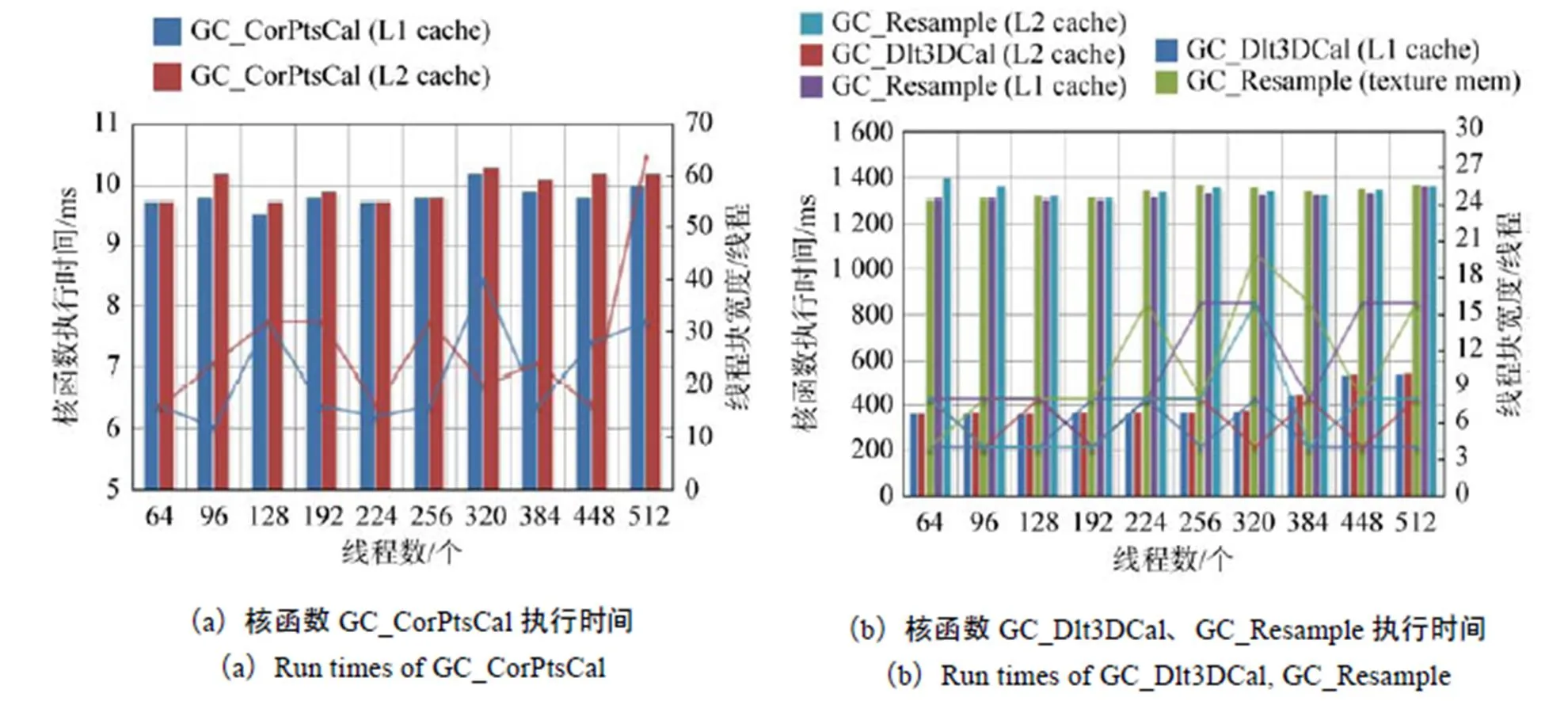
图6 改变线程块大小、形状和缓存模式时核函数执行时间

表3列出了核函数性能优化后的配置、执行时间和性能提升比。可以看出，经过性能优化后，3个核函数的性能都得到不同程度的提升，其中GC_Resample的性能提升比最高，达到了18.1%。

表3 核函数性能优化后的配置、执行时间和性能提升比

Tab.3 Configurations, run times and performance improvement ratios after kernel performance optimization

完成核函数性能的优化配置后须进行整体流程性能优化，通过流机制实现传输计算堆叠，进一步提高整个正射校正的执行效率。表4为分别创建2、3、4个流时，方法执行时间和性能提升比。从表中可知，创建2个流和3个流时，正射校正的性能得到小幅提升，其中创建2个流时性能提升比最高（6.45%），创建4个流时，性能不但没有提升，反而下降（−7.05%）。造成该现象的原因是，当创建多个流时，CPU→GPU数据传输量多于不使用流时。如图7所示，当不创建流时，对输出子影像（图7（b）中影像蓝色框标识区域）进行重采样需要从显存载入对应的输入子影像（图7（a）中影像蓝色框标识区域）；当使用2个流时，每个流负责对一半的输出子影像（图7（b）中影像黄色和绿色标识区域）进行重采样，但此时输入影像会发生叠掩（图7（a）中影像黄色和绿色标识区域发生重合）。这种由于使用流而引入的冗余数据传输极大影响了正射校正的执行效率，并且流的数量越多，冗余传输的数据量越大，因此算法性能不仅没有进一步提升，反而出现下降。

表4 整体性能优化后的方法执行时间和性能提升比

Tab.4 Run times and performance improvement ratios after overall performance optimization

最终经过整体性能优化，GPU上分块三维直接线性变换正射校正的执行时间压缩至5.13s，与CPU逐点坐标转换正射校正方法、CPU分块三维直接线性变换正射校正方法相比，加速比分别达到142.42倍、61.26倍（如表5所示），可以满足对大数据遥感影像的快速处理需求。进一步将文献[9]、[10]中提出的GPU并行处理方法应用至本文，由于仅进行了GPU基本映射，未进行性能优化，因此其执行时间仅为5.62s；文献[3]在文献[9]、[10]的基础上进行了线程块大小和形状的选取优化，因此其执行时间提升至5.51s。综合比较，由于本文提出的方法进行了更加充分、全面的性能优化，因此执行效率更优。

表5 三种方法的执行时间和加速比

Tab.5 Run times and speedup ratios of three ortho-rectification methods

3 结束语

本文系统地探讨了基于分块三维直接线性变换和GPU并行的遥感影像快速正射校正方法。首先针对正射校正坐标转换计算量过大的问题，提出了分块三维直接线性变换策略，有效地降低了坐标转换的计算量，在求解三维直接线性变换模型参数时，引入了虚拟同名点的概念，通过增加方程个数确保模型参数可解。然后，采用“渐进式”策略开展GPU并行处理，提高了方法的执行效率。在Intel Xeon E5650 CPU和NVIDIA Tesla C2050 GPU组成的实验环境中，使用本文方法对“高分二号”卫星全色影像进行实验，发现引入分块三维直接线性变换后，CPU上正射校正执行时间从730.61s压缩至314.24s，加速比为2.33倍；进一步将算法映射至GPU并进行性能优化后，执行时间缩短至5.13s，最终加速比达到142.42倍，可以满足对大数据遥感影像的快速正射校正需求。

随着高性能计算技术的快速发展，GPU计算架构和型号会持续演变更新，新的计算架构加入了一些新功能（例如动态并行、线程格网管理等），使得并行处理方式更加灵活，但GPU底层的硬件设计、执行框架（线程组织）、层次性存储结构未发生明显改变。因此，本文方法可以为基于新计算架构的GPU进行正射校正提供借鉴。此外，近年来，众核CPU、加速处理器（APU）等高性能处理硬件已逐渐发展成熟，因此可以研究正射校正在上述硬件上的并行处理方法，并逐步探索其余遥感数据处理瓶颈算法的并行处理技术。

[1] 杨靖宇. 摄影测量数据GPU并行处理若干关键技术研究[D]. 郑州: 信息工程大学, 2011. YANG Jingyu. Study on Parallel Processing Technologies of Photogrammetry Data Based on GPU[D]. Zhengzhou: Information Engineering University, 2011. (in Chinese)

[2] 蒋艳凰, 杨学军, 易会战. 卫星遥感图像并行几何校正算法研究[J]. 计算机学报, 2004, 27(7): 944-951. JIANG Yanhuang, YANG Xuejun, YI Huizhan. Parallel Algorithm of Geometrical Correction for Satellite Images[J]. Chinese Journal of Computers, 2004, 27(7): 944-951. (in Chinese)

[3] 方留杨, 王密, 李德仁. CPU和GPU协同处理的光学卫星遥感影像正射校正方法[J]. 测绘学报, 2013, 42(5): 668-675. FANG Liuyang, WANG Mi, LI Deren. A CPU-GPU Co-processing Orthographic Rectification Approach for Optical Satellite Imagery[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(5): 668-675. (in Chinese)

[4] 于英, 张元源, 薛武. 基于CUDA的核线影像并行生成技术[J]. 测绘通报, 2013(7): 27-29. YU Ying, ZHANG Yuanyuan, XUE Wu. Epipolar Image Parallel Generation Technology Based on CUDA[J]. Bulletin of Surveying and Mapping, 2013(7): 27-29. (in Chinese)

[5] 杨靖宇, 张永生, 李正国, 等. 遥感影像正射纠正的GPU-CPU协同处理研究[J]. 武汉大学学报·信息科学版, 2011, 36(9): 1043-1046. YANG Jingyu, ZHANG Yongsheng, LI Zhengguo, et al. GPU-CPU Cooperate Processing of RS Image Ortho-rectification[J]. Geomatics and Information Science of Wuhan University, 2011, 36(9): 1043-1046. (in Chinese)

[6] JAVIER R S, MARIA C C, JULIO M H. Geocorrection for Airborne Pushbroom Imagers[J]. IEEE Transactions on Geoscience and Remote Sensing, 2012, 50(11): 4409-4419.

[7] 侯毅, 沈彦男, 王睿索, 等. 基于GPU的数字影像的正射纠正技术的研究[J]. 现代测绘, 2009, 32(3): 10-12. HOU Yi, SHEN Yannan, WANG Ruisuo, et al. The Discussion of GPU-based Digital Differential Rectification[J]. Modern Surveying and Mapping, 2009, 32(3): 10-12. (in Chinese)

[8] 李娜, 白勇, 赵慧洁, 等. 基于多核CPU和GPU的高光谱数据并行几何校正[J]. 现代电子技术, 2013, 36(2): 110-112. LI Na, BAI Yong, ZHAO Huijie, et al. Hyperspectral Data Parallel Geometry Correction Based on Multicore CPU and GPU[J]. Modern Electronics Technique, 2013, 36(2): 110-112. (in Chinese)

[9] 侯明辉, 邱虎. 基于GPU的高分辨率星载SAR系统几何校正[J]. 现代雷达, 2013, 35(9): 40-44. HOU Minghui, QIU Hu. High Resolution Space-borne SAR Geometric Correction Based on GPU[J]. Modern Radar, 2013, 35(9): 40-44. (in Chinese)

[10] 杨景辉, 程春泉, 张继贤, 等. GPU支持的SAR影像几何校正大规模并行处理[J]. 中国图像图形学报, 2015, 20(3): 374-385. YANG Jinghui, CHENG Chunquan, ZHANG Jixian, et al. GPU Supported Massively Parallel Processing for Geometric Correction of SAR Imagery[J]. Journal of Image and Graphics, 2015, 20(3): 374-385. (in Chinese)

[11] 李德仁, 王树根, 周月琴. 摄影测量与遥感概论[M]. 2版. 北京: 测绘出版社, 2008. LI Deren, WANG Shugen, ZHOU Yueqin. An Introduction to Photogrammetry and Remote Sensing[M]. 2nd ed. Beijing: Surveying and Mapping Press, 2008. (in Chinese)

[12] KIRK D B, HWU W M W. Programming Massively Parallel Processors[M]. Amsterdam: Elsevier, 2010.

[13] NVIDIA. CUDA C Best Practices Guide, v5.0[Z]. Santa Clara: NVIDIA Corporation, 2012.

[14] NVIDIA. Fermi Hardware and Performance Tips[Z]. Santa Clara: NVIDIA Corporation, 2011.

[15] SANDES J, KANDROT E. An Introduction to General-purpose GPU Programming[M]. Boston: Addison-wesley Professional Press, 2010.

[16] 潘腾, 关晖, 贺玮. “高分二号”卫星遥感技术[J]. 航天返回与遥感, 2015, 36(4): 16-24. PAN Teng, GUAN Hui, HE Wei. GF-2 Satellite Remote Sensing Technology[J]. Space Recovering & Remote Sensing, 2015, 36(4): 16-24.

[17] VOLKOV V. Better Performance at Lower Occupancy[EB/OL]. [2018-03-27]. http://www.nvidia.com/content/GTC-2010/ pdfs/2238_GTC2010.pdf.

A Fast Remote Sensing Image Ortho-rectification Method Based on Block-wise Transformation and GPU Parallel Processing

FANG Liuyang1HE Hongyan2,3ZHANG Bingxian2

（1 National Engineering Laboratory for Surface Transportation Weather Impacts Prevention, Broadvision Engineering Consultants, Kunming 650041, China）（2 Beijing Institute of Space Mechanics & Electricity, Beijing 100094, China）（3 Beijing Key Laboratory of Advanced Optical Remote Sensing Technology, Beijing 100094, China）

Ortho-rectification is one of the most computationally and time-consuming steps in remote sensing data processing, and has become a bottleneck restricting the rapid completion of remote sensing data processing. Therefore, a fast ortho-rectification method, based on block-wise three-dimensional linear transformation and GPU parallel processing, is proposed in this paper. First, a three-dimensional linear transformation is introduced to reduce the computational amount of coordinate projection conversion. Then, based on progressive strategy, the GPU parallel mapping (including kernel mapping and basic settings) is conducted. Furthermore, two performance optimization methods, i.e., kernel performance optimization and overall performance optimization, are used to further improve the efficiency. The approach is tested with GF-2 panchromatic images with CPU and GPU. The experimental results show that the processing time is only 5.13 s, with a speedup ratio of 142.42, which can meet the requirement of fast ortho-rectification for big-data-volume remote sensing images.

ortho-rectification; block-wise three-dimensional linear transformation; GPU parallel mapping; kernel performance optimization; overall performance optimization; processing of remote sensing image data

P237

A

1009-8518(2018)06-0080-11

10.3969/j.issn.1009-8518.2018.06.010

2018-03-27

国家自然科学基金（41601476）

方留杨，男，1987年生，2015年获武汉大学测绘遥感信息工程国家重点实验室摄影测量与遥感博士学位，高级工程师。主要从事遥感数据处理、交通灾害防治应用等研究工作。E-mail：fangliuyang@stwip.com。

（编辑：夏淑密）