超声速条件下伞盘模型的气动干扰数值研究

戴刚 薛晓鹏



超声速条件下伞盘模型的气动干扰数值研究

戴刚 薛晓鹏

（中南大学航空航天学院，长沙 410083）

盘缝带降落伞是目前已成功实施的火星着陆任务均采用的主流伞型，为了探究盘缝带伞衣中不同的伞盘模型形状对于降落伞性能的影响，文章基于计算流体力学方法针对不同构型的伞盘模型进行数值模拟研究，分析和预测其超声速条件下的气动性能表现。结果表明：随着伞盘模型凹陷深度的减小，伞前脱体激波更接近伞体，导致伞内表面驻点区域的压力变大；当伞盘凹陷深度增大时，气流从伞端部流出时更容易使得端部压力升高，因此获得更大的平均压力分布，导致其阻力系数增大，然而这也会引起可观的侧向力，使得伞衣稳定性降低。另外，当来流马赫数增大，其阻力系数会随之减小。该结果对于火星降落伞的伞形的设计有一定的参考价值。

盘缝带伞 盘模型 超声速流 数值模拟 火星探测

0 引言

迄今为止，美国向火星发射了多颗探测器，其中部分已经成功在火星表面着陆，在火星探测器减速着陆过程中降落伞是不可或缺的气动力减速装置[1]。从“海盗号”（Viking）到最近的“火星科学实验室”（Mars Science Laboratory，MSL），这些成功降落在火星表面的探测器所使用的降落伞系统均为盘缝带降落伞（Disk-Gap-Band Parachute，DGB Parachute）[2-4]。自20世纪60年代开始，就有众多研究者针对盘缝带降落伞展开了研究[5-16]，其中文献[7]对Viking型盘缝带降落伞10%的缩比模型进行了风洞试验研究，发现阻力系数最小值出现在马赫数为1.0的情况下，随马赫数继续增加，阻力系数最大增加了20%。文献[8]通过整理NASA不同超声速降落伞的风洞试验数据，对比分析了在火星低密度的大气条件下盘缝带降落伞具有较好的减速特性与稳定性。文献[9，10]针对伞盘面积相对较小的MPF（Mars Pathfinder）型降落伞和伞盘面积相对较大的Viking型降落伞进行了风洞试验，分析显示MPF型降落伞阻力系数较小，稳定性较好。另外，随着计算机和数值模拟方法的发展，利用数值模拟技术针对火星降落伞的研究成为了可能。文献[11]通过求解三维可压缩 Navier-Stokes方程发现，存在伞缝的半球形伞体的伞前激波较无缝伞体更贴近伞体端口，导致该区域压力分布增加，并且由于缝隙的存在使得伞内压力显著下降。文献[12]基于一种简易“浸入边界技术”与流固耦合方法，分析了攻角范围在0°~10°的带有伞绳的刚性半球体伞型系统的流动特性及其对伞体性能的影响，发现伞体的气动特性受到拖曳距离比的影响，阻力系数有随着攻角增加而增大的趋势。文献[13]使用大涡模拟模型计算了柔性有伞缝的三维薄壳降落伞的流固耦合过程，在超声速条件下观测到了伞衣的呼吸现象。文献[14]采用风洞试验和数值模拟技术分析比较超声速来流下刚性凸形平板和凹形平板的流场，发现凹形平板相比于凸形平板阻力较大、稳定性较低。文献[15]数值模拟了马赫数为4.0的刚性半球形伞体流场情况，观测到了伞体周围流场的非定常特性，发现随着时间的推进，半球形伞前激波由最初的轴对称小幅度脉动模型演变为完全非轴对称的大幅度脉动变化。

总之，在高马赫数条件下，不同的降落伞伞盘模型有着不同的流场分布和流动特性，特别是盘缝带降落伞的阻力特性以及稳定性与其结构有着重要的关系。但是目前尚没有针对降落伞的不同伞盘构型对于阻力特性以及稳定性影响的研究，本研究将在现有盘缝带降落伞系统的基础之上，利用数值模拟技术探索不同形式伞盘的气动特性和阻力性能表现。

1 伞盘模型

本研究仅针对伞盘结构进行数值模拟研究，不考虑降落伞系统中前体（太空舱）以及伞带和缝隙造成的气动干扰。本研究通过分析流场分布情况确定伞衣的稳定性与阻力来源，为便于与前期研究中的日本航空航天局（JAXA）的风洞试验结果作对比[11]，将降落伞伞盘简化为刚体模型，并采用试验中的尺寸。

针对常见的半球形伞型与近平板式的滑翔伞型，结合火星降落伞最常用的盘缝带降落伞伞型，对4种具有代表性的伞盘模型进行研究，如图1所示，在半球形伞盘模型基础上分别取伞口角为90°、60°、30°以及0°（伞盘的半径趋近于∞，即为平板）的情况下，通过改变，保证其投影面积=0.011 3m2条件。对4种不同的伞盘模型进行数值计算。为描述方便，分别定义伞盘 A、B、C、D，各伞盘形状详细尺寸如表1所示。

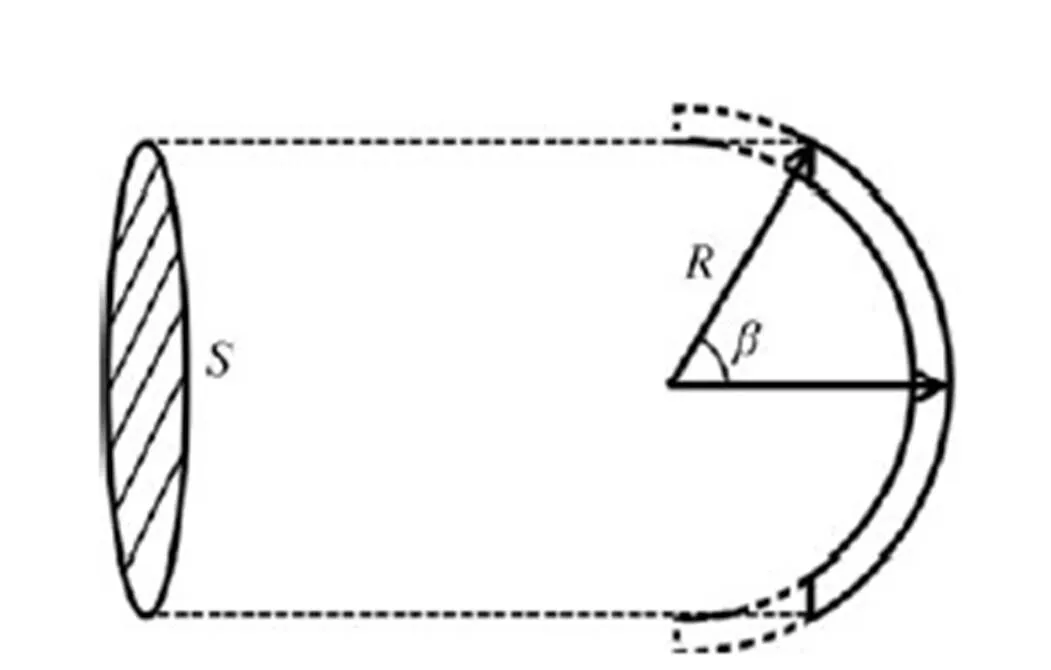
Fig.1 The canopy disk model used in this study

表1 4种伞盘尺寸

Tab.1 The size of the four canopy disk models

2 数值计算

2.1 模型简化

通过改变伞口角度所得到的伞盘如图2所示。当由90°变化至0°时，其最主要的变化为伞盘内部的凹陷深度减小。4种伞盘全部为轴对称模型，为简化计算，本研究对模型子午线截面进行数值模拟。在保证一定的准确性的同时，可以相应地减少计算资源的使用。

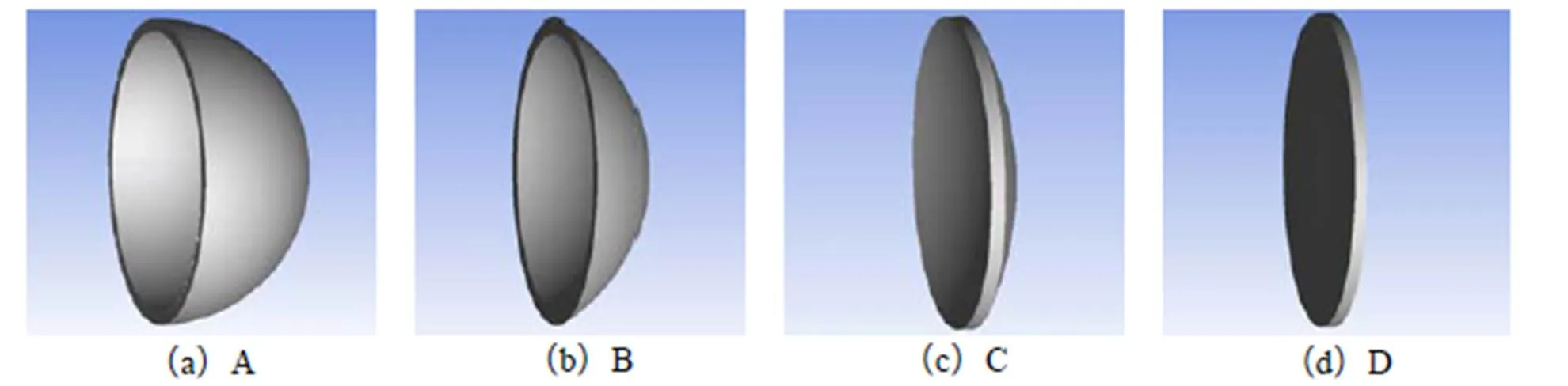
图2 不同伞盘的3-D模型

2.2 数值模拟验证

本研究数值计算中的来流条件如表2所示，该来流条件来源于文献[16]的风洞试验条件。计算网格采用结构网格，4个伞盘的近壁面网格划分如图3所示。伞盘A、B、C、D数值模拟计算网格数目分别为87 724、78 224、65 480、76 220，所用网格数与文献[17]网格结构密度相似，并且此类密度的网格已经获得了比较好的数值模拟结果。4组模型最小网格间距都为0.008mm。

表2 本文研究计算所用的来流条件[16]

Tab.2 Free stream conditions employed in this study

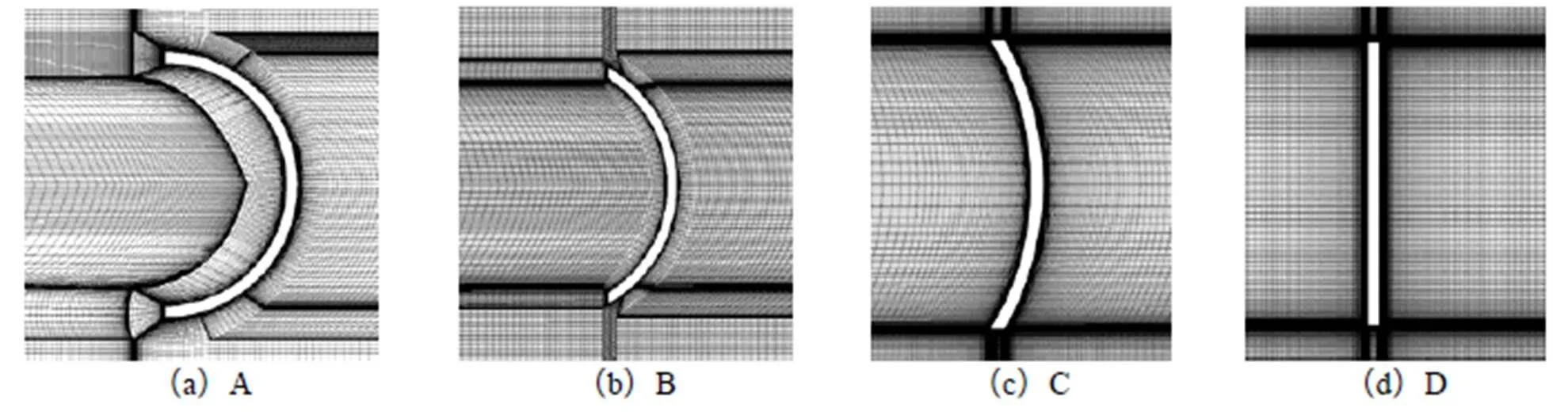
图3 不同伞盘的近壁面网格划分

本研究使用CFD++14.0软件进行计算，采用基于密度解算器，计算方程选用可压缩理想气体N-S方程，模型采用Spalart-Allmaras（SA）一方程湍流模型，非定常瞬态格式，时间推进采用2阶TVD隐式推进。伞盘A的内表面压力分布与试验数据对比如图4所示。图4中伞内、外表面位置标度用/表示，其中为伞内、外表面距离中心的弧线长度，为伞内、外表面最大弧长，以伞内、外表面中心为原点。数值模拟结果与JAXA风洞试验结果[16]相差在2%以内。该数值模拟方法适用于本文来流条件下的超声速降落伞的数值模拟。

3 数值模拟结果分析

由于火星降落伞的主要开伞速度在马赫数为2.0左右，本研究参考了文献[3]中美国NASA进行的盘缝带刚性降落伞风洞试验中的来流马赫数（=2.0、2.2、2.5），为了较为系统地分析不同伞盘模型的气动性能表现，基于以上验证的数值模拟方法对伞盘A、B、C、D分别进行来流=2.0、2.2、2.5的数值模拟计算，计算过程中保持=2.04×107[17]。

3.1 不同伞盘模型的气动表现

在来流=2.0的情况下，4种伞盘的内表面压力分布如图5所示，伞盘A、B的内表面压力分布表现较为均衡，驻点区域压力与周围压力大小相近；伞盘C内表面高压力分布区域开始集中于靠近驻点位置；而伞盘D驻点区域的压力更是明显高于远离对称轴位置压力。

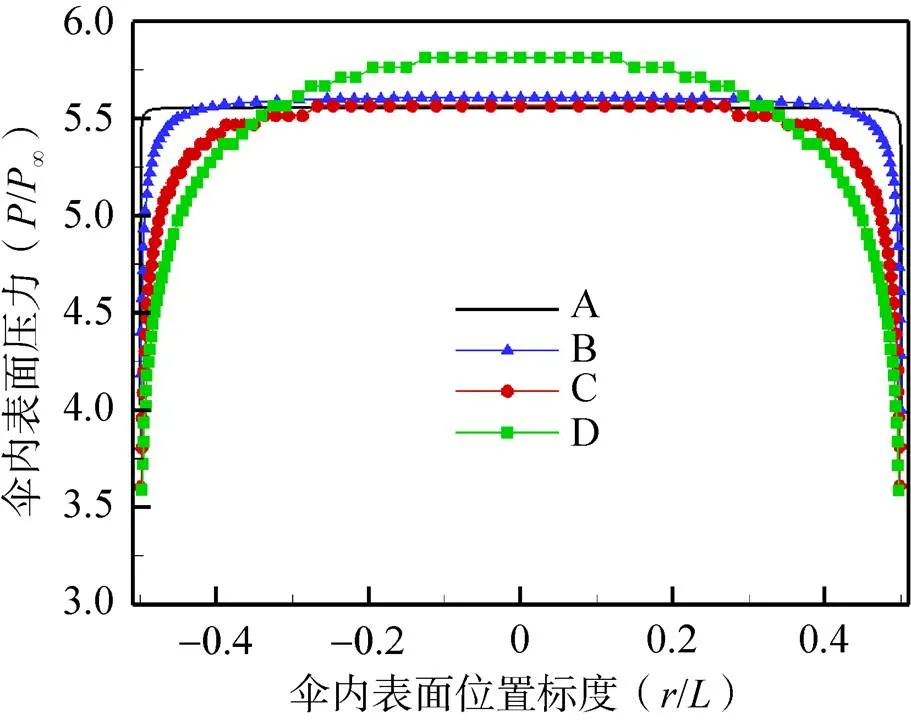
图5 Ma=2.0不同伞盘的内表面压力分布

各伞盘流场压力分布及流线分布如图6所示。可以看出，4种伞盘流场分布相似，其中高压力区域（红色区域）面积大小表现为伞盘A>B>C>D；伞盘C与D的内表面的驻点区域相对较窄，压力分布相对集中。从流线分布来看，伞形A中伞内驻点区域分布在伞体的轴对称中心下侧，这会造成伞内流场分布不均匀，从而使得压力分布不对称。通过对数值模拟结果（见图5）的计算分析，伞体内表面位置标度为正的部分，平均压力比为5.417 0，位置标度为负的部分平均压力比为5.403 2，这必然导致在流动过程中产生可观的侧向力，从而使得伞体的稳定性降低。在三维情况下，由于三维的叠加效应，该不平衡现象可能会更加明显。相比之下，其他伞盘均观测到较为对称的流场分布，所以凹陷深度较浅的伞盘具有较好的稳定性。

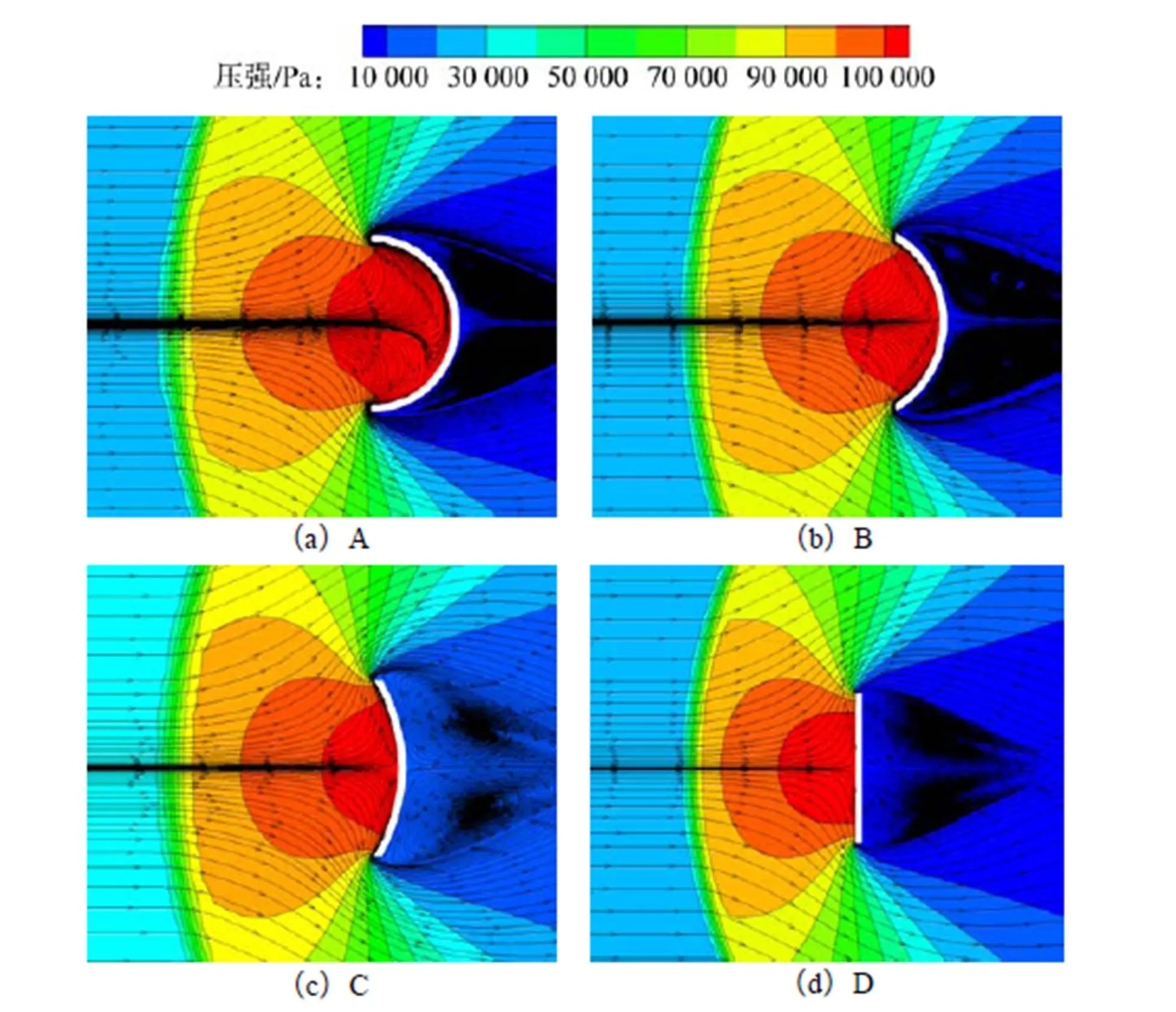
图6 Ma=2.0来流条件下4个不同伞盘模型的瞬时流场

降落伞的减速作用通常由阻力表征，该阻力作用在来流方向，可由伞体表面的内外压力差计算。在超声速流场条件下，表征该阻力的阻力系数d[18]定义为

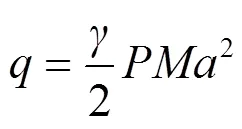
各伞盘的阻力系数如图7所示。另外，图7中还对比了不同伞盘的伞前激波的脱体距离（用/表示，其中为激波位置至伞体中心点距离；为伞体端口对应弦长）。从图7中可以看出，伞盘A的阻力系数为1.871，与相同来流条件下的JAXA风洞试验[16]结果中的1.64相差在15%以内。此外，从图7还发现，随着凹陷深度的减小（角度减小），伞前脱体激波更接近伞体，这导致伞体内表面驻点区域的压力变大。但是，当伞体凹陷深度增大，气流从伞体端部流出时更容易使得该部位压力升高，从而获得更大的平均压力分布，导致其阻力系数增大。

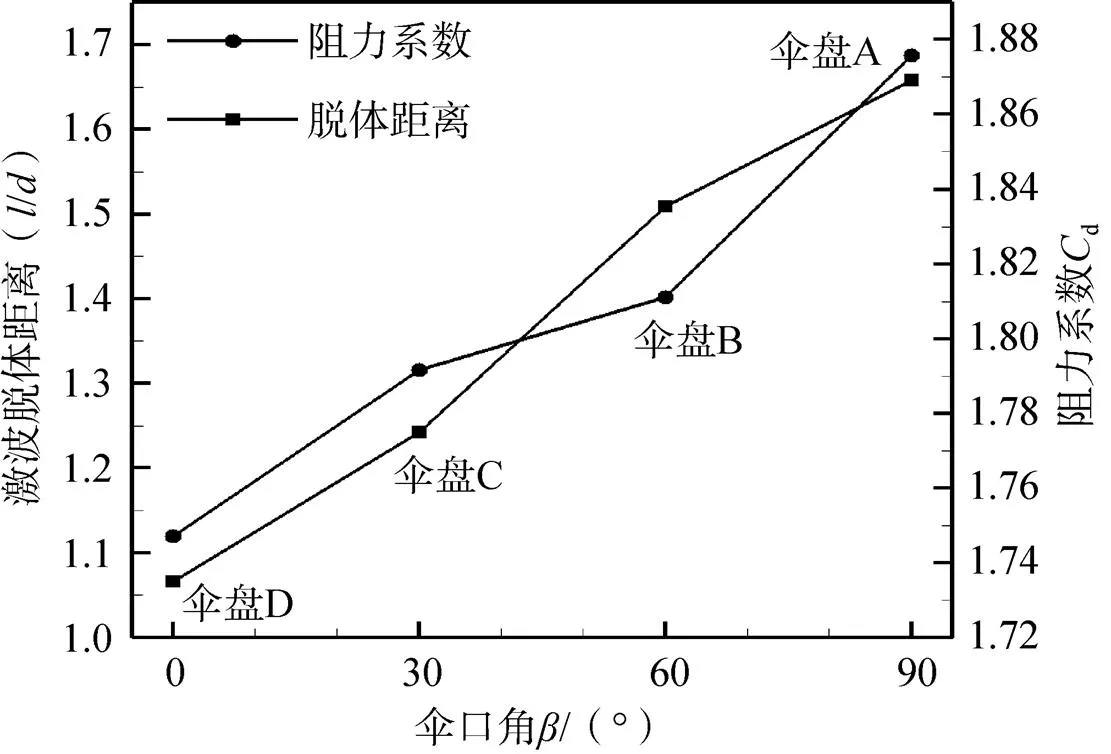
图7 Ma=2.0时各伞盘的阻力系数与脱体距离

3.2 不同来流马赫数的影响

伞盘A、B在不同马赫数下的压力分布云图如图8所示。通过比较发现，当来流马赫数逐步增加时，伞前激波会更加靠近伞体入口，且激波锥度逐渐减小，而伞盘C、D流场表现与此类似。该结果与文献[3]中NASA刚性盘缝带伞风洞试验中激波锥度随马赫数变化规律相同。另一方面，当来流马赫数增大时，伞体内表面的压力随来流马赫数增大而增大（如图9所示）。伞盘外表面压力随来流马赫数变化情况如图10所示，对于伞盘D马赫数由2.0增大至2.2时，外表面压力变化不明显，有较小的降低趋势，其他伞盘外表面压力均随来流马赫数增大而增大。

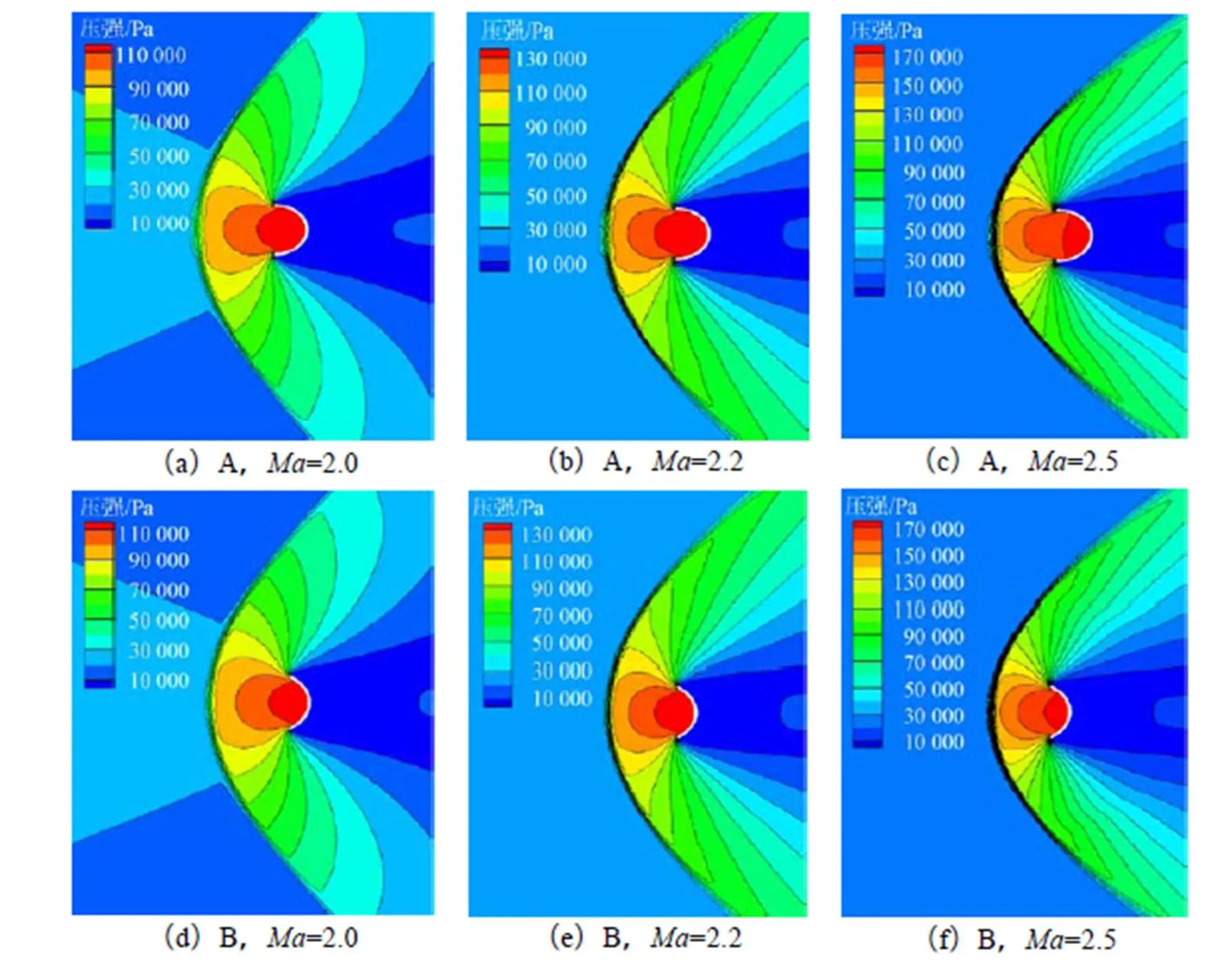
图8 伞盘A、B在不同来流马赫数下的压力分布

图9 不同马赫数下的各伞盘内表面压力分布

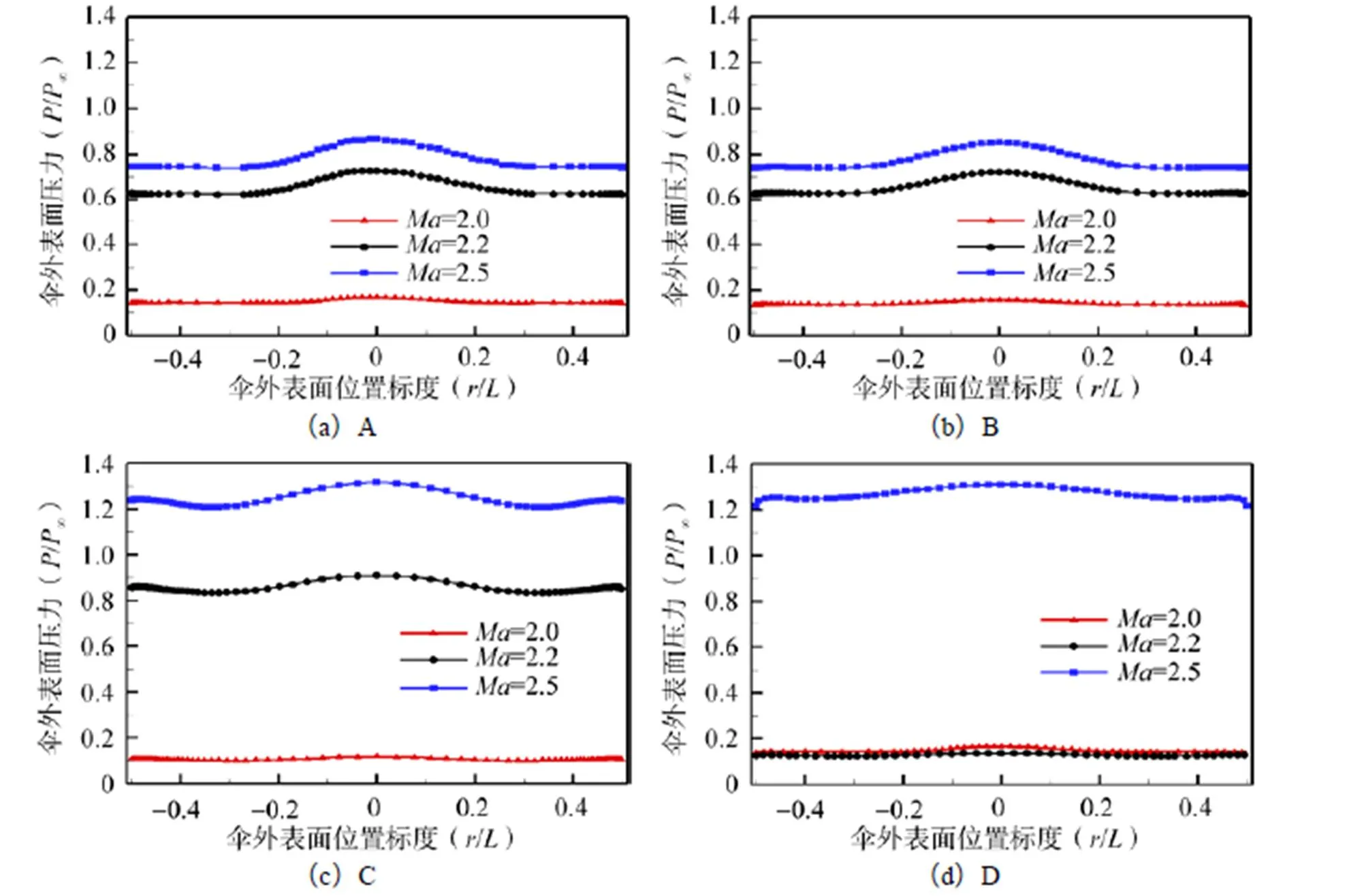
图10 不同马赫数下的各伞盘外表面压力分布

不同来流马赫数下伞盘A、B、C、D的阻力系数与脱体距离比较如图11所示，由图可知，随着马赫数的增加，虽然伞体内表面的压力增大，但伞体外表面的压力同样也随马赫数的增加而增大，阻力系数反而有减小的趋势，在超声速条件且落地距离满足要求的情况下，应尽量选择在较小的马赫数下开伞。此外，虽然伞体内表面的压力增大，但是来流的动压增加更为明显，相比之下伞体对激波的阻碍作用减弱，所以在马赫数增加的情况下，其脱体距离在逐渐减小。图11所示的阻力系数与脱体距离变化规律与文献[3]中NASA刚性盘缝带伞风洞试验中不同马赫数阻力系数变化规律相同，可见不同盘模型在高马赫数变化时的阻力性能表现保持一致。

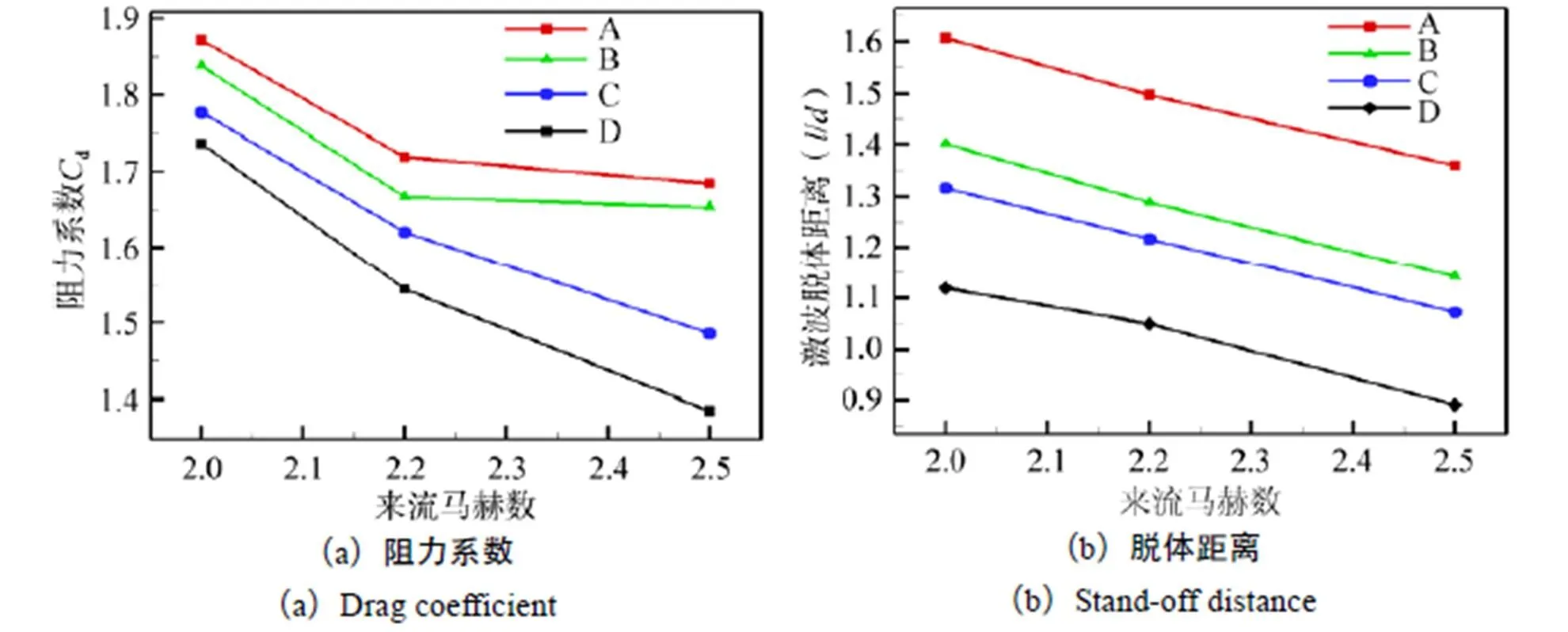
图11 不同来流马赫数下的各伞盘的阻力系数和脱体距离变化

4 结束语

本文利用计算流体力学方法对4种伞盘模型的流场分布情况以及气动性能表现进行了数值分析。

在不考虑前体尾流以及伞带和缝隙的气动干扰作用下，超声速流过伞盘时，随着凹陷深度的减小（即伞口角的逐渐减小），脱体激波更接近伞体，引起伞内表面驻点区域的压力变大。但是，当伞盘凹陷深度增大时，气流流动距离变长，因此端部气流流出时更容易使得该部位压力升高，平均压力分布增大，进而获得较大的阻力系数，表现出更好的减速特性；然而由于气流流动距离增大以及伞内流场的不均匀分布会导致可观的侧向力，造成伞衣稳定性降低。另外，当来流马赫数增大，伞前激波锥度减小，且脱体距离减小，伞内外表面的压力均随来流马赫数增大而增大，其阻力系数则随之减小。

因此，在实际应用中需要根据任务类型以及着陆方式选择降落伞凹陷深度以兼顾降落伞的减速作用与稳定性，即针对超声速条件下工作的降落伞设计中，通过设计伞口角度减小侧向力，同时选择伸展率较高的材料作为伞衣材料，或者进行伞内的曲面设计，增大伞体中部的凹陷程度，达到增加伞衣面积、提升减速性能的效果。同时在保证稳定减速效果的前提下尽量在较小的速度条件下开伞。下一步研究拟通过实物风洞试验进行进一步验证，使其更具工程说服力。在此基础上再考虑前体的气动干扰，研究不同伞形系统的减速与稳定特性。

[1] BRAUN R D, MANNING R M. Mars Exploration Entry, Descent and Landing Challenges[C]//2006 IEEE Aerospace Conference. Big Sky, MT, USA: IEEE, 2006: 310-323.

[2] 于莹潇, 田佳林. 火星探测器降落伞系统综述[J]. 航天返回与遥感, 2007, 28(4): 12-16. YU Yingxiao, TIAN Jialin. Mars Explorer's Parachute System Overview[J]. Spacecraft Recovery & Remote Sensing, 2007, 28(4): 12-16. (in Chinese)

[3] SENGUPTA A, STELTZNER A, COMEAUX K, et al. Results from the Mars Science Laboratory Parachute Decelerator System Supersonic Qualification Program[C]//2008 IEEE Aerospace Conference. Big Sky, MT, USA: IEEE, 2008: 1-15.

[4] 李爽, 江秀强. 火星进入减速器技术综述与展望[J]. 航空学报, 2015, 36(2): 422-440. LI Shuang, JIANG Xiuqiang. Review and Prospect of Decelerator Technologies for Mars Entry[J]. Acta Aeronautica ET Astronautica Sinica, 2015, 36(2): 422-440. (in Chinese)

[5] LEMKE R A, MORONEY R D, NEUHAUS T J, et al. 65 Foot Diameter D-G-B Parachute, Planetary Entry Parachute Program: NASA-CR-66589[R].[S.l.]: United States, 1967.

[6] ECKSTROM C V, PREISSER J S. Flight Test of a 30-Foot-Nominal-Diameter Disk-Gap-Band Parachute Deployed at a Mach Number of 1.56 and a Dynamic Pressure of 11.4 Pounds per Square Foot: NASA TM X-1451[R].[S.l.]: United States, 1967.

[7] STEINBERG S Y, III P M S, SLAYMAN R G. Development of the Viking Parachute Configuration by Wind-tunnel Investigation[J]. Journal of Spacecraft & Rockets, 1973, 11(2): 101-107.

[8] CRUZ J, LINGARD J. Aerodynamic Decelerators for Planetary Exploration: Past, Present, and Future[C]//AIAA Guidance, Navigation, and Control Conference and Exhibit. Washington, DC, United States: American Institute of Aeronautics and Astronautics, 2006.

[9] 高树义, 戈嗣诚, 梁艳. 火星盘缝带伞跨声速风洞试验研究[J]. 中国空间科学技术, 2015(4): 69-75. GAO Shuyi, GE Sicheng, LIANG Yan. Research on Transonic Wind Tunnel Tests of Mars Disk-gap-band Parachutes[J]. Chinese Space Science and Technology, 2015(4): 69-75. (in Chinese)

[10] CRUZ J, MINECK R, KELLER D, et al. Wind Tunnel Testing of Various Disk-gap-band Parachutes[C]//17th AIAA Aerodynamic Decelerator Systems Technology Conference and Seminar, May 19-22, 2003. Monterey, California: AIAA, 2003: 1-16.

[11] 薛晓鹏. 超声速降落伞系统非定常气动干涉的数值模拟[C]//第十七届全国激波与激波管学术会议. 成都: 中国空气动力研究与发展中心, 2016. XUE Xiaopeng. Numerical Simulation of Unsteady Aerodynamic Interaction of a Supersonic Parachute System[C]//The 17th National Shockwave and Shockwave Conference. Chengdu: China Aerodynamics Research and Development Center, 2016. (in Chinese)

[12] 薛晓鹏, 温志湧, 汪运鹏, 等. 不同攻角下超声速降落伞伞绳的影响研究[J]. 航天返回与遥感, 2017, 38(4): 47-54. XUE Xiaopeng, WEN Chihyung, WANG Yunpeng, et al. Effects of Suspension Lines on the Supersonic Parachute System at Different Angles of Attack[J]. Spacecraft Recovery & Remote Sensing, 2017, 38(4): 47-54. (in Chinese)

[13] KARAGIOZIS K, KAMAKOTI R, CIRAK F, et al. A Computational Study of Supersonic Disk-gap-band Parachutes Using Large-eddy Simulation Coupled to a Structural Membrane[J]. Journal of Fluids & Structures, 2011, 27(2): 175-192.

[14] VASHISHTHA A, WATANABE Y, SUZUKIK. Study of Shock Shape in front of Concave, Convex and Flat Arc in Hypersonic Flow[C]//Proceedings of the 46th Fluid Dynamics Conference/32nd Aerospace Numerical Simulation Symposium. Hirosaki, Aomori, Japan: JAXA, 2015: 127-132.

[15] HATANAKA K, RAO S M V, SAITO T, et al. Numerical Investigations on Shock Oscillations Ahead of a Hemispherical Shell in Supersonic Flow[J]. Shock Waves, 2016, 26(3): 299-310.

[16] NISHIYAMA Y. Aerodynamic Characteristics of the Supersonic Parachute with Its Opening Process[D]. Nagoya: Master Thesis of Nagoya University, 2013.

[17] XUE X, KOYAMA H, NAKAMURA Y. Numerical Simulation of Supersonic Aerodynamic Interaction of a Parachute System[J]. Transactions of the Japan Society for Aeronautical & Space Sciences Aerospace Technology Japan, 2013, 11: 33-42.

[18] SENGUPTA A, KELSCH R. Supersonic Performance of Disk-gap-band Parachutes Constrained to a 0-degree Trim Angle[J]. Journal of Spacecraft and Rockets, 2009, 46(6): 1155-1163.

Numerical Simulation of Aerodynamic Interaction of Canopy Disk Models Under Supersonic Conditions

DAI Gang XUE Xiaopeng

（School of Aeronautics and Astronautics, Central South University, Changsha 410083, China）

Disk-gap-band parachutes have been mainly applied in the last successful Mars landing missions. In this paper, the numerical simulations of the disk models with different configurations are conducted to analyze and predict the aerodynamic performance of different disk models under supersonic conditions by using computational fluid dynamics (CFD) methods. As a result, it was found that as the depth of canopy concave become smaller, the shock ahead of the canopy comes closer to the canopy with a shorter stand-off distance, which causes the pressure of the stagnation point on the inner surface of the canopy become higher. When the concave depth of the canopy is larger, the flow strenuously escapes from the canopy inner, where the fluid is pressurized, and the higher pressure can be observed on the entire canopy surface, which leads to a larger drag coefficient. However, the higher pressure around the canopy edge part may cause considerable lateral force which leads to the poorer stability. In addition, when the freestream Mach number increases, the drag coefficient decreases. The above results will provide a reference for the design of the Mars parachute.

disk-gap-band parachute; disk model; supersonic flow; numerical simulation; Mars exploration

V445

A

1009-8518(2018)06-0012-09

10.3969/j.issn.1009-8518.2018.06.002

2018-04-26

国家自然科学基金（11702332）

戴刚，男，1996年生，2018年获中南大学航空航天学院航空航天工程专业学士学位，现于浙江大学航空航天学院攻读博士学位。研究方向为流体力学。E-mail：daigang_csu@163.com。

薛晓鹏，男，1982年生，2013年获日本名古屋大学航空航天工程专业博士学位，副教授。研究方向为气动力减速器技术数值计算方法。E-mail：xuexiaopeng@csu.edu.cn。

（编辑：夏淑密）