考虑桩后及桩侧土拱间相互作用的合理桩间距
陈 龙,刘成禹,2,林雪彬,缪昊
(1.福州大学 环境与资源学院, 福建 福州 350108;2.地质工程福建省高校工程研究中心, 福建 福州 350108)
随着铁路、公路和市政建设的发展,出现了大量的高边坡与滑坡,抗滑桩为高边坡与滑坡治理的最主要工程措施之一。抗滑桩属于横向受荷(水平荷载)桩,在水平荷载作用下,桩土间相互作用在桩间形成土拱效应,土拱效应形成是抗滑桩间距设计的重要依据[1-3]。土拱范围直接关系到土拱的传力特性和抗滑桩支护效果。为此,许多学者对土拱进行了研究[4-7]:有些学者研究表明,抗滑桩背部作为拱脚,形成桩后土拱传递滑坡推力到桩身;另外一些学者研究表明,除了桩后土拱,桩土界面通过摩阻力的支撑也能形成桩侧土拱,来传递滑坡推力。因此,在桩后土拱前缘处还存在桩侧土拱。
目前抗滑桩间距的确定,滑坡规范给出桩间距建议的范围,没有给出桩间距计算公式[8]。桩间距计算公式主要通过假设桩间不同成拱形式推导而来。目前推导桩间距公式的方法,主要有3种:第一种方法仅考虑桩后土拱,根据桩间静力平衡条件以及土拱拱顶、拱脚的破坏准则,建立桩间距计算公式[9-10]。第二种方法仅考虑桩侧土拱,根据桩侧面摩阻力不小于滑坡推力以及土拱拱顶、拱脚的破坏准则,建立桩间距计算公式[11]。第三种方法同时考虑桩后、桩侧土拱,根据桩后、桩侧土拱的极限平衡条件,建立桩间距计算公式[12-13]。上述计算方法中,方法1、2均存在桩间土拱考虑不全的缺点,认为桩后土拱或桩侧土拱单独承担滑坡推力,使得计算出的合理桩间距与实际情况存在一定的偏差;方法3考虑了两土拱共同作用,却忽略了由桩侧面摩阻力提供给桩后土拱的抗滑力,这样,虽然是基于两土拱确定出的合理桩间距,但会偏于保守。
本文基于抗滑桩既有桩后土拱又有桩侧土拱的桩间成拱形式,合理的计算出桩侧土拱提供给桩后土拱的抗滑力,在此基础上计算合理的桩间距。
1 计算模型
抗滑桩截面形状常为矩形。为此,本文以矩形截面抗滑桩为例进行分析。
1.1 基本假设
(1) 在抗滑桩间距为最佳桩间距时,桩后土拱与桩侧土拱联合并存,联合的土拱可分解为两个单独的土拱[14]。
(2) 两单独拱所受推力之和等于桩后滑坡推力。
(3) 桩间土拱主要为水平土拱,桩后土拱与桩侧土拱均符合合理拱轴线,作用在两者上的推力均为均匀分布,且作用范围近似为相邻两桩净间距[9-10]。
(4) 在合理桩间距下,桩后土拱与桩侧土拱处于极限平衡状态。
依据上述假定,建立分析简图,如图1所示。图中,p为桩后滑坡推力,a为抗滑桩截面宽度,b为抗滑桩截面高度,L为相邻两桩净间距。
1.2 桩后土拱与桩侧土拱受力分析
根据上述假定,沿桩深方向取单位高度土拱进行受力分析,如图2所示。
为清楚表示桩后、桩侧土拱的参数,下文中:下标为1的代表桩后土拱参数,下标为2的代表桩侧土拱参数。
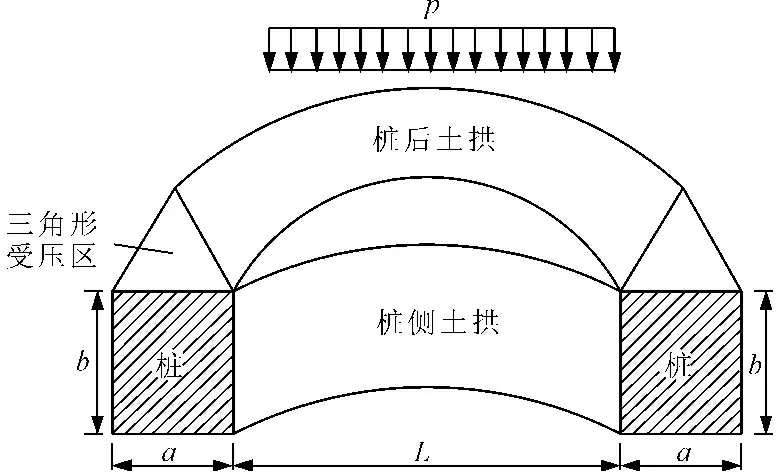
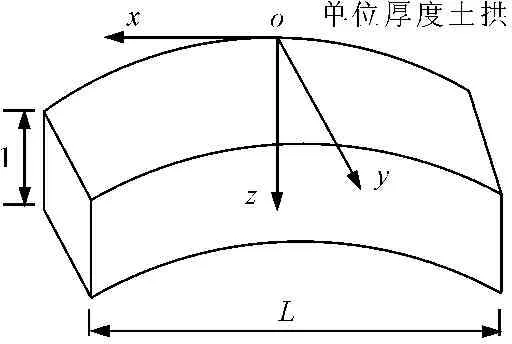
图1 抗滑桩截面土拱模型
图2单位高度土拱
1.2.1 桩后土拱受力分析
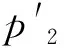
图3单位高度桩后土拱受力模型
1.2.2 桩侧土拱受力分析
单位高度桩侧土拱受力简图,如图4所示。根据基本假设(2),两单独拱所受推力之和等于桩后滑坡推力,土拱不向桩前土体传递桩后滑坡推力,故不考虑桩前土体提供的反力;与桩后土拱一样,忽略土拱自身产生的剩余下滑力。因此,桩侧土拱在y轴方向上受到桩后土拱向前传递的剩余滑坡推力p2以及桩侧摩阻力Fy2的共同作用。
结合以上两单独拱受力分析的基础上,根据基本假设(2)有:
(1)
消去式两边的L有:
p1+p2=p
(2)
式中:p1与p2分别为桩后土拱与桩侧土拱上所承载的均布推力。
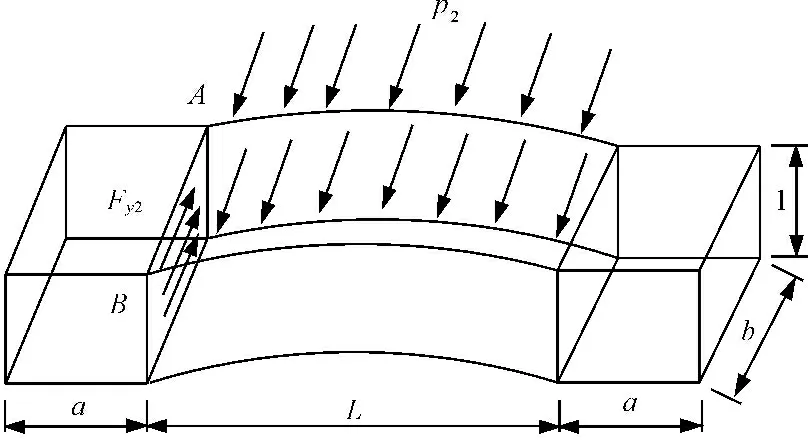
图4单位高度桩侧土拱受力模型
1.3 合理拱轴线
合理拱轴线为跨中对称的抛物线,在均布荷载作用下,可取一半进行受力分析,如图5所示。图5中,q为合理拱轴线在y轴方向上承载的均布推力,Fx为拱脚与拱顶的水平力,Fy为拱脚竖向力,f为拱高。

图5合理拱轴线模型
合理拱轴线上任意截面无剪力,只有轴向压力,根据结构力学的“三铰拱”模型,拱轴线方程为:
(3)
由静力平衡条件可知拱脚处的水平与竖向力为:
(4)
由于桩后土拱与桩侧土拱均为合理拱轴线,上述的力学模型对两者均可适用,下文在使用式(3)、式(4)时,仅需调整相对应的符号,公式形式并无改变。
2 合理桩间距计算公式
2.1 桩侧土拱与桩后土拱的相互作用力
在剩余滑坡推力作用下,桩侧土拱处于极限平衡状态时,土拱将沿着桩土界面发生剪切破坏[16],如图6所示。图6中,AB面为剪切破坏面,其上作用着法向力Fx2和摩阻力Fy2,AC面为拱脚截面,作用在其上的力可为本文1.3章节合理拱轴线拱脚处的反力,F2为拱脚反力的合力,α2为合理拱轴线在拱脚位置处轴向切线与水平线的夹角。
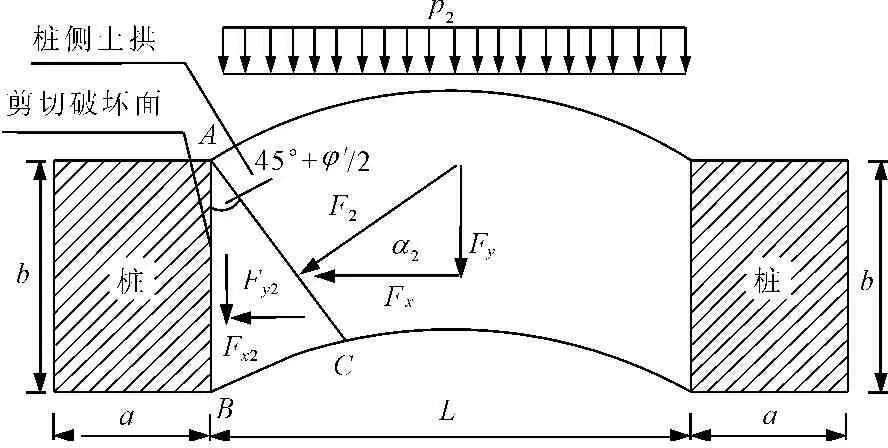
图6桩侧土拱拱脚破坏平面图
对拱脚处的ABC隔离分析,由静力平衡可得:
(5)
(6)
式中:f2为桩侧土拱拱高。在破坏面AB上,依据摩尔-库仑破坏准则,可建立如下方程:
(7)
式中:φ′与c′分别为桩土界面的摩擦角与黏聚力,当桩侧土为细粒土时[17],取φ′=φ/2或φ′=2φ/3,c′=ctanφ/tanφ′。
将式(5)、式(6)代入式(7)中得:
(8)
由极限平衡理论可知大主应力作用面与破坏面的夹角为α2=45°+φ′/2;在拱轴线x=L/2处的切线斜率为:
(9)
由式(8)、式(9)联立得出桩侧土拱的极限承载力为:
(10)
由力的相互作用可知,桩侧土拱提供给桩后土拱的抗滑力为:
(11)
2.2 桩后土拱的极限平衡条件
桩后土拱处于极限平衡状态时,邱子义等[12]、刘小丽等[18]认为土拱沿着K点水平方向发生破坏,如图7所示。图7中桩后均存在三角形受压区,左侧拱的桩后受压区为EFG,EF的长度t1为桩后土拱的厚度;K为EF的中点,即拱轴线与拱脚截面的交点。

图7桩后土拱拱脚破坏平面图
在K点,土体沿水平方向发生剪切破坏,由极限平衡理论得:
(12)
由三角形受压区几何关系得:
(13)
拱轴线在x=L/2处的切线斜率为:
(14)
式中:f1为桩后土拱拱高。
由于桩后土拱跨中截面为最不利截面,同时拱顶前缘M点(见图7)相对后缘点更加不利,因此前缘点要满足强度条件[10]。
基于以上讨论,本文重点考虑抗滑桩受荷段底端的土拱跨中前缘M点的三向应力状态。其中,M点水平面内的应力为σx和σy,σx为桩后土拱拱顶处的轴向压应力,σy为桩侧土拱对桩后土拱的反力,竖向应力σz可由受荷段底端的土体自重应力算出,因此,M点三向应力表达式为:
(15)
式中:H为抗滑桩受荷段长度。
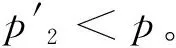
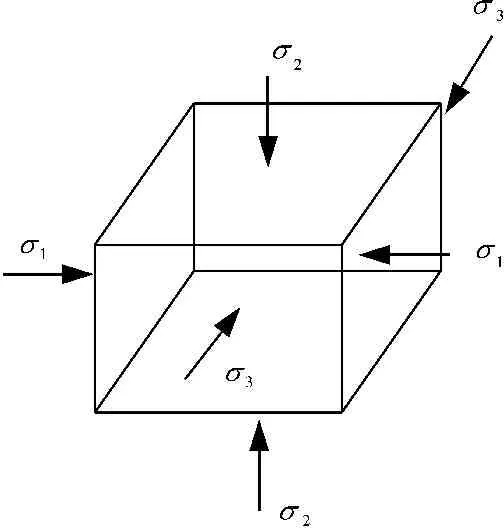
图8M点三向应力
2.3 合理桩间距计算公式
根据M点三向应力状态,并结合俞茂宏统一强度理论有[19]:
(16)
式中:β为统一强度参数,反映中间主应力影响的权参数,一般取为0<β<1,本文取为β=1/2,统一强度能替代D-P准则。σt为土体拉伸强度极限,ω为土体拉压强度比,根据摩尔-库仑准则得:
(17)
(18)
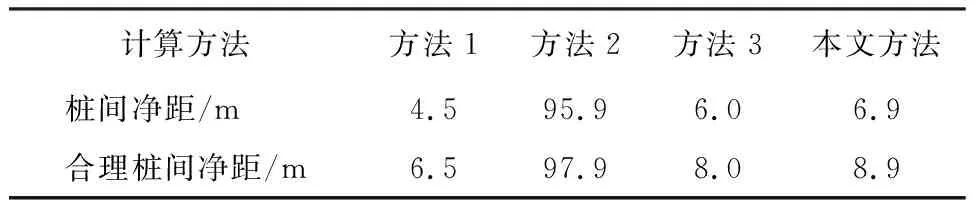
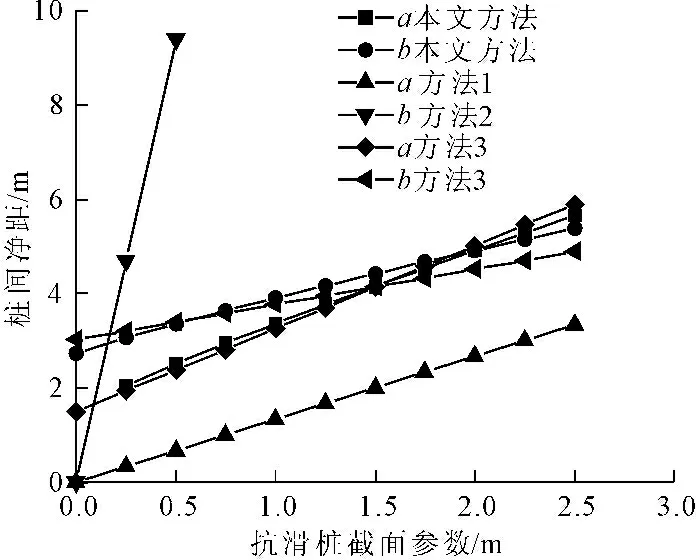
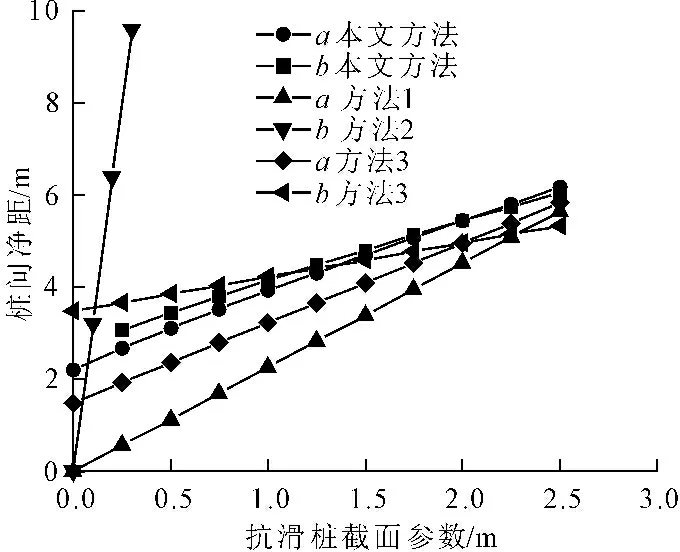
式(16)中需判断σ2与(σ1+ωσ3)/(1+ω)大小关系,以确定使用式(16)中的第一式还是第二式。为判断两者大小,笔者引入俞茂宏等[20]和Lee等[21]研究成果:σ2=m(σ1+σ3)/2,m为中间主应力系数,0 综上所述,本文将式(2)、式(11)、式(12)、式(13)、式(14)、式(15)、式(17)、式(18)代入式(16)中的第二式得: (19) 式(19)中的桩后滑坡推力沿桩身分布形式应根据实际工程选择。上式得出的结果为桩间净距,合理桩间距应为:S=L+a。 为了更好地说明本文方法的合理性和适用性,本文选择2种类型的滑坡体的工程案例进行分析,工程案例一的滑坡体为黏土和粉质黏土,工程案例二的滑坡体为碎石土。具体计算如下: (1) 工程案例一。案例引自文献[9],滑坡体为黏土和粉质黏土为主夹杂碎石,坡体倾斜度为20°,土体重度γ=18 kN/m3,土体抗剪强度参数c=130 kPa,φ=15°,抗滑桩截面尺寸a=2 m,b=3 m,抗滑桩受荷段长H=10.5 m。由不平衡荷载传递系数法计算出抗滑桩处的设计滑坡体推力为1 076.6 kN/m。 抗滑桩处滑动面与水平面的夹角为20°,滑坡推力的水平分力为:Fh=1076×cos20°=1011.7 kN/m。滑坡体主要以黏土与粉质黏土为主,受荷段滑坡推力沿桩身按三角形分布[22-24]。因此,在受荷段底端的单位高度的滑坡推力为: 桩土界面的摩擦角与粘聚力为: 将以上参数代入式(19)中,得桩间净距为:L1=5.8 m;合理桩间距为:S1=L+a=7.8 m。 (2) 工程案例二。案例引自文献[10],滑坡体以碎石土为主,土体抗剪强度参数c=80 kPa,φ=30°,抗滑桩截面尺寸a=2 m,b=3 m,抗滑桩受荷段长H=8 m。由不平衡荷载传递系数法计算出抗滑桩处的设计滑坡体推力为560 kN/m。由于文献[10]中没有给出土体重度,在此设其重度为γ=18 kN/m3。 滑坡体主要以碎石土为主,受荷段滑坡推力沿桩身按矩形分布[22-24]。因此,在受荷段底端的单位高度的滑坡推力为: 桩土界面的摩擦角与黏聚力为: 将以上参数代入式(19)中,得桩间净距为:L2=6.9 m;合理桩间距为:S2=L+α=8.9 m。 目前确定合理桩间距时,各算法都做了不同的假设,例如:赵明华等[9]认为桩间仅形成桩后土拱,忽略桩侧土拱存在(方法1);郑磊等[11]认为桩间仅形成桩侧土拱,忽略桩后土拱存在(方法2);邱子义等[12]考虑了桩后、桩侧土拱同时存在,却忽略由桩侧面摩阻力提供给桩后土拱的抗滑力(方法3)。 将本文工程案例一、案例二分别用于上述方法中进行计算,结果列于表1、表2中。并与本文算法比较。 表1 工程案例一各算法结果对照表 表2 工程案例二各算法结果对照表 从表1、表2可以看出: (1) 由于忽略桩侧土拱存在,方法1得出的结果,相较于方法3以及本文方法,会偏于保守。 (2) 由于忽略桩后土拱存在,方法2得出的结果,相较于方法3以及本文方法,会偏于过大。 (3) 本文方法在方法3基础上多考虑了桩侧反力的影响,其计算结果比方法3稍大。 (4) 本文通过对桩侧土拱静力平衡分析,合理的计算出桩侧土拱提供的抗滑力,在此基础上得到的合理桩间距均符合《滑坡防治工程设计与施工技术规范》[8](DZ/T 0219—2006)建议桩间距5 m~10 m的范围,因此本文算法可适用性高。 分析式(19)可知桩-土参数对桩间净距选取影响较大,其影响参数主要为a、b、φ、c、c′、φ′和t1。但在一个实际工程中,土体参数是确定的,而桩体截面参数可以任意改变,使得桩体截面参数对桩间距布置相对于土体参数影响更大。因此,笔者将重点讨论抗滑桩截面参数a、b对抗滑桩桩间距布置的影响。 图9、图10表示方法1—方法3以及本文方法的a-L、b-L关系曲线图,图9、图10的数据由上述工程案例一、案例二控制单一变量得到。 图9 工程案例一抗滑桩截面参数-桩间净距关系图 图10工程案例二抗滑桩截面参数-桩间净距关系图 从图9、图10可以看出: (1) 方法1的桩间净距与抗滑桩截面宽度均呈线性增函数关系。由于忽略桩侧土拱存在,因此,桩间净距仅与抗滑桩截面宽度有关这有悖于实际情况。 (2) 方法2的桩间净距与抗滑桩截面高度均呈线性增函数关系。由于忽略桩后土拱存在,因此,桩间净距仅与抗滑桩截面高度有关,这也与实际情况不相符。 (3) 方法3以及本文方法中桩间净距与抗滑桩截面宽度、高度都相关,呈线性增函数关系。其中,b-L曲线斜率相对于a-L曲线斜率小,表明桩间净距对抗滑桩截面宽度的变化更为敏感。 (1) 本文通过对桩侧土拱静力平衡分析,得到桩后土拱受到来源于桩侧土拱提供的抗滑力,比以往研究更加合理。在此基础上得到的合理桩间距,相较于已有的计算方法,能有效的节约经济。 (2) 通过分析各算法中桩体截面参数对桩间净距影响,认为敏感性顺序:b>a,更符合桩体截面敏感性关系。因此,桩体截面b则应成为工程设计中重点考虑的因素。 (3) 目前基于土拱效应建立桩间距计算公式时,都做了不同的假设,计算公式的适用性受到一定程度的限制。迫切需要适用于普遍条件的统一桩间距计算公式。
3 不同方法对比分析
3.1 工程案例
3.2 计算方法对比分析
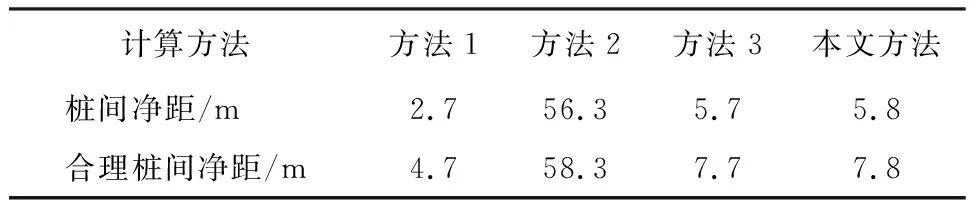
3.3 桩间净距随桩截面尺寸的变化
4 结 论

