考虑时间效应和剪切模量变化的基桩负摩阻力分析

张 鹏，李洪强

(1.中国电建集团 华东勘测设计研究院有限公司， 浙江 杭州 311122；2.浙江广川工程咨询有限公司， 浙江 杭州 310020)

在我国东南沿海地区广泛分布着近代沉积形成的淤泥质软黏土，其具有土层深、含水率高、压缩性大，承载力低等特点。随着经济发展和生活需求，大量的高层建筑、厂房、桥梁坐落在软弱土基之上，为了满足工程建设需求，需要对地基进行大面积堆载预压处理，同时通过打设桩基将上部荷载传递到地基深部强度高的土层上，提供更高的承载力并减少基础沉降和不均匀沉降。

在工程实际中发现许多桩基础建筑物在设计荷承载力高于实际使用荷载若干倍的情况下，仍会产生由于不均匀沉降导致建筑物开裂无法使用的现象。经调查研究发现当桩身周围的土体的固结沉降大于桩基沉降时，桩身承受向下作用的摩擦力，这部分向下的摩擦力叫负摩阻力。桩身负摩阻力出现的条件主要有：桩端部支撑于较硬的土层中而桩身穿过欠固结土层；桩使用过程中地面大面积堆载导致沉降过大；临近场地地下水位降低引起有效应力增加而导致大面积地区性下沉等。

负摩擦阻力的出现会给桩基带来许多不利的因素：如桩基承载力降低、桩基础沉降增加和桩身强度的安全储备减小等。因此深入研究软基础下桩基负摩阻力分布规律及其计算方法具有及其重要的工程实际意义。

从20世纪30年代开始国内外学者工程师就对负摩阻力进行试验和理论研究，取得了很多成果。研究主要集中在：理论研究方面，利用线性协调[1]、力的平衡[2-3]、弹性理论[4-5]等方法计算摩阻力的分布；利用荷载传递法预测单桩负摩阻力分布；试验方面主要通过桩摩阻力现场试验[6-10]和室内模拟试验[11-12]两种方式测出中性点的位置和摩阻力的分布；利用有限元方法计算摩阻力的分布[13-14]。上述方法中现场原位试验法费工费时、耗资巨大。而有限元法需要确定很多的参数，计算起来不方便。

本文根据桩-土间的相互作用机理，采用桩土荷载传递法建立了考虑时间效应和剪切模量随深度变化两种因素下的软黏土地区桩负摩阻力的计算模型，为工程设计和工程应用提供参考。

1 负摩阻力产生机理

一般情况下负摩阻力的出现是由于桩身的上半部分桩周土体沉降大于桩体本身沉降负摩阻力才会出现，负摩阻力只分布在桩身的一部分，其余部分产生与桩身位移相反的正摩阻力。由于摩阻力分布是连续的，所以在同一根桩身上由负摩阻力过渡到正摩阻力间存在一个摩阻力为零的横断面，该断面成为中性点。在中性点以上土体沉降大于桩的位移，在中性点一下土体位移小于桩体位移；在中性点以上负摩阻力方向与位移方向一致，中性点以下负摩阻力方向与位移方向相反。在实际工程施工中桩顶的荷载和地面堆载作用往往不是同时施加的。一般情况下负摩阻力桩的加载次序往往先是在桩顶先施加荷载，引起土体沉降的外部作用(地面堆载，地下水位下降等)之后施加。在桩顶荷载作用下，桩的大部分沉降在很短的时间内就可以完成，而地面堆载作用下的土体固结沉降过程需要很长的时间才能完成。因此负摩阻力需要历经一个缓慢的时间过程才能逐渐发挥出来，所以文中对负摩阻力分布进行分析时考虑时间因素的影响。

2 负摩阻力计算公式和模型

2.1 堆载作用下的地基沉降分析

引起桩周土体沉降的因素很多，最主要的是地下水位的下降和地面堆载两种因素，都是由于有效应力的增加而导致土体产生新的固结沉降。本文按照堆载预压条件进行分析，对地基进行大面积堆载预压土体因受荷载作用而发生固结，一般条件下外荷载作用保持不变，因此在地基任一深度z处附加总应力p(z)为常数。在施加荷载的瞬时，p(z)全部由土中的孔隙水来承担，经过时间t后，孔隙水压力消散，其值变为u(z，t)，此时有效应力的增量为p(z)-u(z，t)，有效应力变化是地基产生固结沉降的主要原因。根据地基沉降的计算理论，可得位于深度为z、厚度为dz的土层，经过时间t后的沉降量为：

ds(z,t)=mv(z)[ps(z)-u(z,t)]

(1)

在大面积堆载作用下，ps(z)沿深度变化不大,在土体压缩层范围内，mv(z)的变化也可视为较小，则式(1)可简化为：

ds(z,t)=mv[ps-u(z,t)]

(2)

大面积堆载作用下，地基内产生的超静水压力可以采用Terzaghi一维固结理论[15]分析：

(3)

(4)

其中：Cv为固结系数；H为土层厚度；ps为作用在地面的堆载荷载。

将式(3)代入式(2)中积分得到：

(5)

2.2 桩的荷载传递

2.2.1 传统的荷载传递函数

图1为所取桩体微单元受力示意图，根据所取微元的竖向平衡条件，可得公式：

qs(z)udz+N(z)+dN(z)-N(z)=0

(6)

化简可得到桩身摩阻力的微分方程：

(7)

其中：A为桩身的横截面积；U为桩身的周长；Ep为桩基自身的弹性模量。

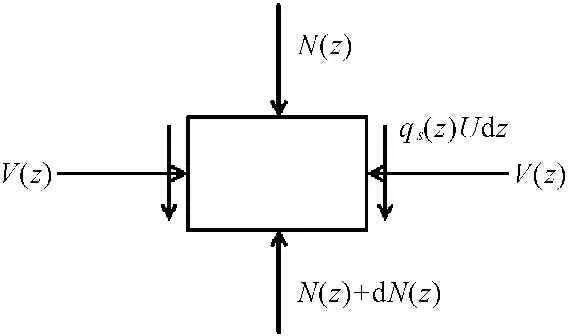
图1桩的微元体受力图

2.2.2 改进的荷载传递函数

由于桩顶荷载和地面荷载不是同时施加的，而是先后施加的。且在地面堆载施加之前，在桩顶荷载作用下的桩沉降已经完成。在地面堆载作用之后，桩的沉降是在桩顶荷载作用下的沉降之后的继续沉降，桩周土体的沉降也是桩顶荷载作用下土体沉降与地面堆载产生的新沉降之间的叠加。因此Alonso等[16]根据Randolph和Worth的模型和边界条件，在极坐标下建立了桩身摩阻力函数的线弹性表达式：

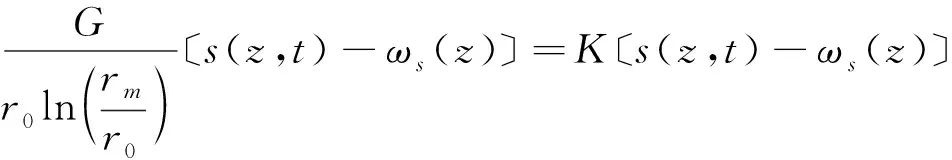
(8)

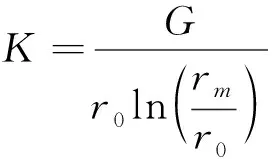
2.3 桩端阻力的传递函数

徐芝纶[18]把桩端荷载简化为一个点荷载作用在无限半空间中，桩端荷载引起的变形可以通过下式表达：

(9)

其中：Sb为桩端位移；Nb为桩端荷载；E为桩周土体的弹性模量。

由于桩不是点荷载，因此引入影响系数Ib。同时桩身弹性模量远远大于土体的剪切模量，因此可得：

(10)

式(10)为考虑时间效应的桩基负摩阻力表达式。

3 考虑剪切模量随深度变化的影响

在固结过程中由于超静孔隙水压力逐渐消散，有效应力增加造成土体被压缩，因此土体的结构趋于密实。周燕国[19]利用弯曲元对砂土进行试验发现剪切模量对土体的结构具有表征作用，即剪切模量可以反映土体结构的变化。Anderson等[20]研究发现，软黏土在固结过程中剪切模量随时间不断增长但增长趋势不同，可以根据固结过程分为两个阶段：主固结阶段和次固结阶段。两者之间存在明显的拐点，可以用曲线的切线和直线段延长线的交点确定。因此在桩基负摩阻力分布计算中不能将剪切模量G的值取为一个常数，而是随固结时间变化的。所以要想准确确定桩基负摩阻力的分布，首先要确定桩基周围土体剪切模量G的变化(见图2)。

图2模量随时间变化示意图(D. G. Anderson)

从图2中可以看出主固结在很短的时间内完成，模量在后续阶段内呈线性增长，因此Anderson等根据这一特性得到了描述模量随时间变化的公式：

(11)

其中：t1，t2为主固结完成后次固结阶段的任意两个时间；ΔG为从t1到t2模量的变化值。

并且得到了现场剪切模量的预测公式：

GField=GPrimary+FA*IG

(12)

其中：GField为现场值的预测值；FA为现场的时间因数；GPrimary是主固结完成时测得的最大动剪切模量。

原位测试点的时间因数FA可通过下式计算：

FA=lg(tc/tp)

(13)

其中：tc为现场测点土在应力历史中最近一次应力开始改变至今所历经时间；tp为现场测点在应力改变后主固结完成的时间。

本文利用共振柱系统分别在围压50 kPa，100 kPa，200 kPa，300 kPa下研究软黏土剪切模量G随时间的变化。试验所用土样为东南沿海典型的淤泥质软黏土，基本物理参数如下：密度ρ为1.7 g/cm3～1.8 g/cm3，含水率为42%～50%，比重Gs为2.71，液限ωL=57%，塑限ωp=26%，黏粒含量为54.6%，细粒含量为92.4%。试验中围压施加后每个试样的试验持续时间为7 d，在这期间每隔一定的时间测量一次土样的共振频率，然后计算得到土体的剪切模量G。

由于篇幅原因只给出了围压为50 kPa，200 kPa下剪切模量随时间变化的曲线图如图3、图4所示。从图中可以看出在初始主固结阶段，剪切模量随时间的延长而急剧增加，这是因为当荷载施加到土体上时，超静孔压力上升，随着时间增加超静孔压力逐渐消散，有效应力增加引起土体空隙的减少；当主固结完成后进入次固结阶段模量随时间呈线性增长关系，这是由于黏土结构的塑性调整和土骨架的硬化所造成的。根据测得的试验结果按照公式(11)计算得到IG，并将IG和围压值标在图5中，从图5可以看出IG与围压P呈明显的线性关系，且随着P的增大而增大。因此可以用关系式表示

IG=20.01P+174.8 (14)

图3 围压50 kPa下模量随时间变化曲线

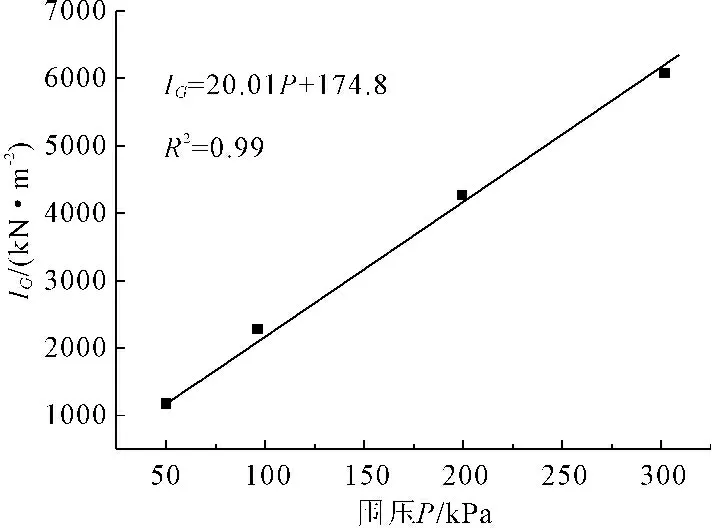
图4 围压200 kPa下模量随时间变化曲线

图5IG与围压关系曲线

图6为主固结时间与围压关系曲线图，从图6中可以看出主固结时间随围压的增大而延长，并且呈非线性关系。主固结完成时间tp与围压P可以用如下公式进行拟合得到：

tp=(4525P-146824)0.5-137.75

(15)

图6主固结时间与围压的关系

将公式(14)、公式(15)代入公式(12)可得场地剪切模量随时间和围压的公式：

GField=GPrimary+

(16)

因此只需测得主固结完成后的剪切模量GPrimary，土层形成的时间tc和该土层深度的围压P，就能得到现场不同深度剪切模量GField的值。将公式(16)所得到的值代入公式(10)即可得到不同深度下桩周负摩阻力的值。

4 工程实例分析

为了验证文中所得公式的正确性，下面就东南沿海地区的某一工程实例进行分析。

某一负摩擦桩现场试桩工程，地基为淤泥质软黏土，土层厚度达43 m，地下水位埋深为2.5 m。上部土层厚度达22 m，土体的密度为ρ=1.75 g/mm3，土的固结系数为Cv=9.318×10-6m2/s；下层土体厚21 m，密度为ρ=1.87 g/mm3，固结系数Cv=5.9832×10-6m2/s。工程采用φ609×11，长50 m的钢管桩，弹性模量Ep=210 000 MPa。场地土承受100 kPa的均布荷载，堆载的面积为45 m×45 m，堆载的历时为295 d。

本次计算中取泊松比为υ=0.35，Ib=0.7，rm=12.5。室内试验测得的主固结完成后的剪切模量为G=0.664 MPa。

图7为根据上节的计算方法得到的理论值，剪切模量G值取恒定得到的理论值与现场实测桩身轴力的比较。其中曲线1为现场实测值，曲线2为剪切模量随深度、时间变化所得的结果，曲线3为剪切模量取恒定值所得结果。

图7桩身摩阻力实测曲线与计算曲线

从图中可以看出，实测的最大桩身轴力为774.9 kN，剪切模量变化所计算得到的最大桩身轴力为804.6 kN，剪切模量取恒定值得到的桩身最大轴力为394.2 kN。其值分别比实测值大3.8%和小49.1%。可以看出剪切模量对计算值影响很大，并且从图上可以看出曲线2与实测曲线吻合度较好。而模量取恒定值得到的曲线与实测值相差较大。这说明在进行负摩擦桩计算式，不但要考虑桩土作用的时间效应，同时也要考虑剪切模量随深度的变化。

5 结 论

本文通过室内试验对软粘土固结特性进行分析得出地基土在不同固结荷载下剪切模量与时间的关系。在此基础上考虑时间因素对剪切模量的影响，建立摩阻力与时间、剪切模量相关的微分方程。

现场实测与理论计算结果表明，本文方法能较准确地描述桩身负摩阻力传递过程以及沿桩身的分布，且计算参数易于获取，是一种可行的基桩负摩阻力分析方法。