基于Logistic回归的砂土地震液化评价

谢 永 宁

(福州大学 环境与资源学院， 福建 福州 350108)

在地震荷载作用下，饱和松砂倾向于收缩，从而使得孔隙水压力急剧升高，相应的有效应力减小。当有效应力非常小甚至为零时，土体会丧失大部分的抗剪强度，从而表现得像液体一样，即为液化。液化会给支撑于土体上面或中间的结构造成巨大的破坏。因此，砂土体地震液化一直是岩土地震工程研究的重点之一。经过过去六十多年的发展，研究人员已经提出众多方法用于砂土地震液化的评价。其中最广泛使用的是Seed和Idriss提出的“简化方法”[1-2]。该方法将现场标准贯入试验(SPT)的击数与砂土体抵抗液化的能力联系起来，并与地震造成的循环剪切应力比进行比较，从而以安全系数的形式判断能否发生液化。基于同一框架，研究人员也尝试将其它现场试验与砂土体抵抗液化的能力联系起来，如静力触探试验(CPT)[3-5]，剪切波速(Vs)[6]等[7]。国内工程实践根据《建筑抗震设计规范》[8](GB 50011—2010)广泛采用标准贯入试验法进行液化的判别[9-12]。

近三十年来，随着计算能力和计算方法的发展，以及越来越多的场地实测数据被收集整理，人们开始尝试采用统计学习的方法进行砂土液化的评价[13-23]。通过把大量数据输入统计学习算法构建学习模型，并将该模型应用于未见过的数据进行预测。得益于最新整理的砂土地震液化数据库[24]，本文利用Logistic回归构建砂土地震液化评价的概率模型，对比分析不同解释变量对模型训练和预测的影响，给出液化概率的显式表达式，并与前人的研究进行对比。

1 Logistic回归

将地震作用下场地液化的概率记为PL(X)，并将其以Logistic函数给出如下：

(1)

其中，X={X1，X2，…Xp}为包含p个解释变量的向量，β={β0，β1，β2，…βp}为模型参数，可通过最大似然函数估计得到。很显然，液化概率PL(X)在0和1之间。记Yi=1和Yi=0分别为液化和非液化的情况，则似然函数L(β)可表示为：

(2)

式中，i=1，2，…，n表示案例数。对式(2)取对数可得对数似然函数：

(3)

通过优化求解L(β)的最大值，即可求得相应的模型参数β。本文通过Limited-memory Broyden-Fletcher-Goldfarb-Shanno(L-BFGS)算法数值求解。

Logistic模型拟合的优劣程度可通过修订似然比指标(MLRI)p2给定[15]：

(4)

2 Logistic回归模型及结果

2.1 数据和解释变量

本文选用的数据源于Boulanger等[23]整理的基于CPT的地震液化记录。该数据库包含从1964年Niigata地震到最近的2011年的日本Tohoku地震等20次地震的253组数据，其中180组有明显的液化现象，71组无液化，并有2组轻微液化，本研究将其看作液化处理。

循环应力比根据Seed-Idriss的简化方法给出如下：

(5)

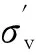
根据文献[24-25]，深度折减因子rd按如下式子给出：

rd=exp[α(z)+β(z)·M]

(6)

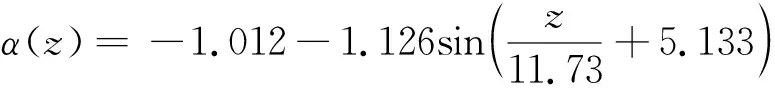
z为所关注土层的深度。

震级缩放因子Fms根据如下式子计算：

(7)

Kσ的计算通过下式给出：

(8)

等效标准化净砂锥尖阻力可通过如下表达式给出：

qc1Ncs=qc1N+Δqc1N

(9)

式中：qc1N=CNqc/Pa为标准化为1个大气压覆土压力下的锥尖阻力；CN为覆土压力修正因子；qc为锥尖阻力；Pa为大气压力(101.3 kPa)；净砂调整项ΔqcqN为细粒含量(Fc)的函数，可给出如下：

(10)

2.2 模型的建立

需要说明的是，本文侧重于Logistic回归模型的预测，因此将选取2010年前的地震数据共196组作为训练集，而将2010后的三次地震(2010年新西兰Darfield地震、2011年新西兰Christchurch地震以及2011年日本Tohoku地震)数据共57组作为测试集。根据前述Logistic回归方法利用训练集训练Logistic模型，然后将此模型应用于测试集，评估其预测效果。

表1 Logistic回归结果

2.3 Logistic回归结果

以液化概率50%作为液化和非液化的判别界限，{q，lnRcs}得到的模型的训练和预测的混淆矩阵如表2所示，当实际类别和预测类别一致时为正确判别，否则为错判。可以看到更多的非液化被错判为液化，这对工程实践而言是有利的，因为实际液化而错判为非液化的后果要比实际非液化而错判为液化的后果严重。训练和预测的准确率分别为85.7%和87.7%，这与Juang等[13]和潘建平等[18]的结果相近。虽然准确率是个非连续变量，但仍可作一定的参考。

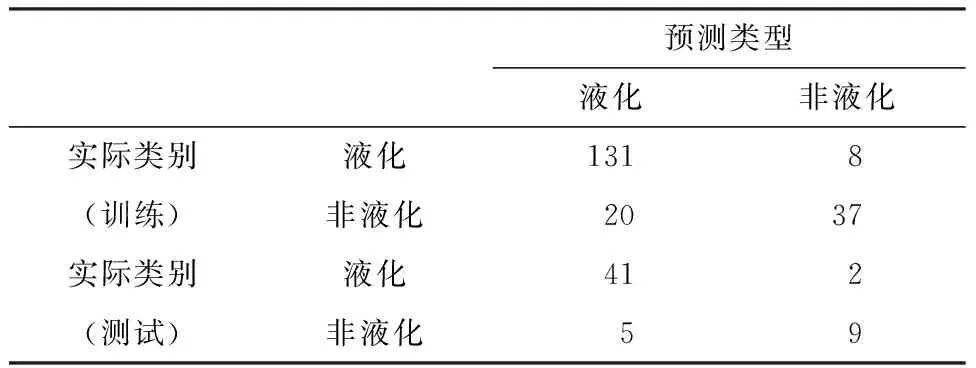
表2 Logistic回归模型的混淆矩阵

用{qlnRcs}作为解释变量得到的模型的液化概率函数为：

图1本文概率模型与其它模型的比较

3 结 论

本文基于最新的砂土地震液化记录，利用Logistic回归构建基于CPT的砂土地震液化评价概率模型，分析对比了不同解释变量对模型训练和测试的影响，得到了液化概率的显式表达式，并与前人的研究结果进行了对比，得出结论如下：

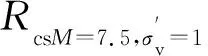
(2) Logistic回归以液化概率50%作为液化和非液化区分时模型的预测准确率为87.7%，这与其他的研究结果相近；虽然准确率为非连续变量，但该结果可作为砂土地震液化确定性分析的一个参考。

(3) 与Boulanger推荐的用于砂土液化确定性分析的曲线相比，本文Logistic回归得到的表达式更为简单，结果也有所不同；具体而言，在qc1Ncs小于90时，Boulanger推荐的曲线要高于本文得到的液化概率50%的曲线；当qc1Ncs介于90到170之间时，该曲线介于本文得到的液化概率50%和30%曲线之间；本文得到的曲线简洁、可靠，工程应用中可根据工程要求选用合适的概率曲线。