蒸发条件下膨胀土裂隙开裂间距和宽度

林 辉，吴华

(南昌航空大学 土木建筑学院， 江西 南昌 330063)

膨胀土吸水膨胀，失水收缩，易产生干缩裂隙[1-2]。蒸发条件下，土体水分丧失，基质吸力增加，土体表面产生张拉力导致开裂，部分能量得以释放，此时的裂隙称之为初始裂隙。若水分继续蒸发，除了初始裂隙继续不断的变宽加深外，有可能在两相邻裂隙之间产生新的裂隙，称之为二次裂隙[3]。由于土体在初次开裂时部分能量已经得到释放，二次裂隙的深度和宽度比初始裂隙的要小，且与初始裂隙有一定的间距，称为二次间距[4]。初始裂隙与二次裂隙混在一起，形成复杂的多边形网格，加速了水分的入渗和蒸发，极大地破坏了土体结构和性能，导致土体强度降低，产生失稳滑坡等工程问题[5]。因此，开展膨胀土开裂问题研究具有重要理论和实际意义。

1 裂隙最大间距和宽度

1.1 受力分析

裂隙产生后，土体的力学形态与开裂之前相比有明显的变化，土体在沿着裂隙面的方向上有着不同程度的收缩，表层土体的收缩变形要大于底层的收缩变形，因此实际裂隙形态多为倒三角形(见图1(a))或梯形(见图1(b))。当土层较薄时，裂隙形态可近似看作矩形。为便于研究，我们假设裂隙形态为矩形，即裂隙顶底部的宽度相同(见图1(c))。

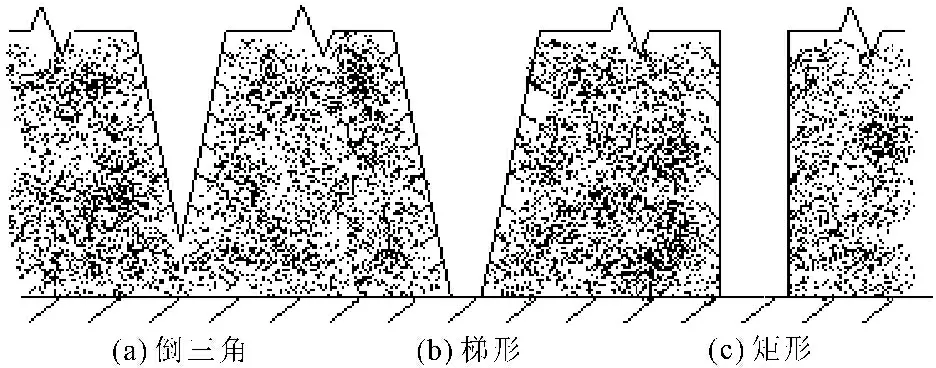
图1常见的裂隙形态

开裂后模型及微体单元如图2所示，裂隙深度为H，相邻裂隙间距为L，以y=0处的平面作为分界面。由于上部土体开裂，裂隙之间的土体有向内侧收缩的趋势，被研究土体在该裂隙面底部x向方向上受到水平力的作用，方向与土体运移趋势方向相反。

图2开裂后计算模型及微体单元

在水平方向x处任取一微体单元，长dx，为简单起见，不考虑微体单元自重及外荷载作用，微体单元承受均匀内力N，底部承受水平剪力Q。由平衡方程∑Fx=0得：

N+dN-N+Q=0，即：dN+Q=0

(1)

式中：dN=bHdσx，b为微体单元宽度；σx为x向应力；Q=τbdx；τ为剪应力。代入式(1)中，得：

(2)

通常情况下，裂隙面处的水平位移最大，两相邻裂隙中间位置的水平位移为零。由土力学原理可知，通常情况下(不考虑剪胀软化)，由于土体能够承受的极限拉应变很小，故可假定裂隙底部处剪切应力τ与该点水平位移u成正比，即令τ=-Cu，C为水平阻力系数，kPa/cm；“-”表示应力与位移的方向相反。

土体任意点的水平位移u由约束位移uσ和变湿位移αΔW·x组成，即：

u=uσ+αΔW·x

(3)

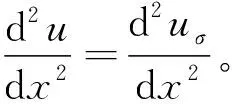
(4)

u=M·ch(Fx)+N·sh(Fx)

(5)

式中：M、N为待定常数；sh(x)、ch(x)分别为双曲正弦、双曲余弦函数。

模型边界条件为：

u=0，x=0；σx=0，x=±L/2

(6)

可求得：M=0，N=αΔW/(F·ch(FL/2))。代入式(5)中，有：

(7)

式(7)即为计算模型底部水平位移的表达式。将其代入由此可求得x向应力σx和剪应力τ分别为：

(8)

1.2 最大间距和最大宽度

式(8)是土体开裂后，裂隙底部x向方向的应力表达式。当土体在距离自由边界(裂隙面)l处的σx达到土体的抗拉强度σt时，在相邻初始裂隙之间将再次开裂。实际工程中，我们关注的是裂隙最终发育的间距和宽度。由于土体的最大x向应力发生在x=0处(相邻裂隙的中间位置)，将x=0代入σx，并令σx=σt，有：

(9)

反解L，可求得裂隙最终发育形成的最大间距Lmax为：

(10)

将x=Lmax代入式(7)中，可得最大宽度δmax的最终表达式：

(11)

式(10)和式(11)是土体开裂后，裂隙最终发育形成的最大间距和最大宽度。最大间距Lmax的物理意义如下：当相邻裂隙的间距l超过Lmax时，其最大x向应力将大于土体的抗拉强度，土体将再次开裂，形成二次裂隙；若二次裂隙与初始裂隙之间的间距仍超过Lmax时，土体仍会开裂，形成多次裂隙，直至裂隙间距小于Lmax。最大宽度δmax的物理意义如下：当相邻裂隙之间不再生成新裂隙时，这两条裂隙的宽度不会超过δmax。土体裂隙附近表层处的水平应力较小，原因在于该处能量的释放及边界自由的缘故。随着与裂隙距离的增加，表层土体约束越来越大，水平应力也不断增大，在相邻裂隙中间位置的水平应力将达到最大。若该处水平应力超过土体的抗拉强度，则该处又会出现裂隙。裂隙生成后，土体能量得到释放，内部应力重新分布，水平应力又小于土体的抗拉强度。随着水分的继续蒸发，水平应力又逐渐增大，若新裂隙与原有裂隙的间距仍大于最大间距，则在其中间位置仍会产生裂隙。若其小于最大间距，则水分的继续蒸发不会在其间形成新裂隙。因此Lmax和δmax实质上反映了裂隙的最终形态，最大间距越大，相应的最大宽度也要大，说明土体越不容易开裂，土体抗裂性能好。因此Lmax和δmax可作为蒸发条件下裂隙最终发育规模的判定依据。

2 参数影响分析

研究表明，最大间距和最大宽度主要受收缩系数、最大变湿、变形模量、抗拉强度、水平阻力系数等因素的共同影响。分析了不同参数对裂隙最大间距Lmax和最大宽度δmax的影响，具体结果见图3～图8。可以看出，在其它参数一定的条件下，随着模量E的增加，Lmax逐渐减小，但变化幅度不大。当胀缩系数α、最大变湿ΔWmax和水平阻力系数C小于某值时，Lmax随着α、ΔWmax、C的增加而急剧减小，表现出典型的非线性特征；当其超过某值时，Lmax的减小速率明显变缓，最终趋于一定值。Lmax随着裂隙深度H和抗拉强度σt的增大而增加，表现出一定的非线性。随着α、ΔWmax、H和σt的增加，δmax逐渐增大，表现为非线性，但非线性程度不明显。δmax随着E的增加而有所增加，但增加幅度不明显。当C小于某值时，δmax随着C的增加而急剧减小；C超过该值时，δmax的减小速率变缓，最终趋于一定值。从图3～图6中我们发现，在一定条件下，土体裂隙的最大间距存在极小值，这表明当裂隙开展到一定程度时，水分的继续丧失仅会导致已有裂隙的加深加宽，不会生成新的裂隙，裂隙形态基本保持稳定。

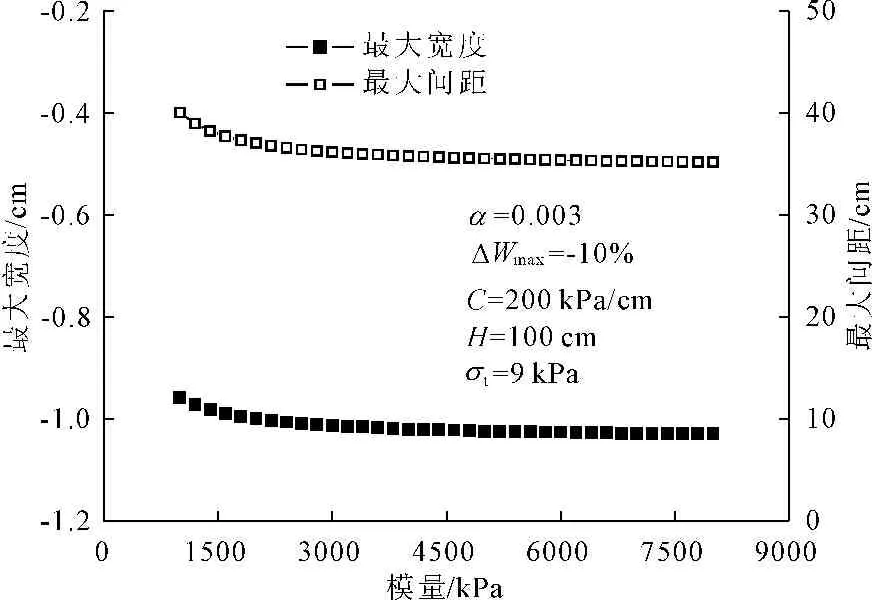
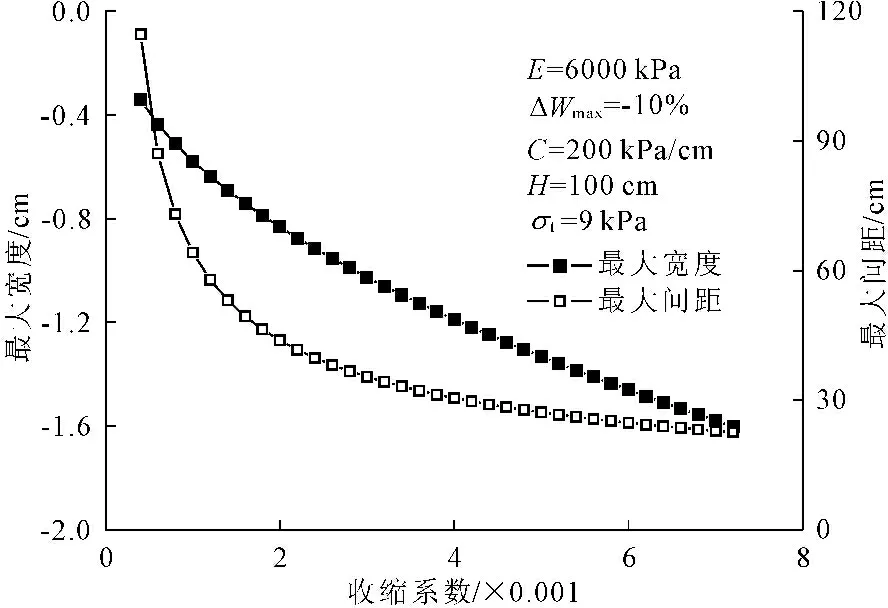
图3 最大间距和最大宽度与模量的关系

图4 最大间距和最大宽度与收缩系数的关系

图5 最大间距和最大宽度与最大变湿的关系

图6 最大间距和最大宽度与水平阻力系数的关系

图7 最大间距和最大宽度与裂隙深度的关系

图8最大间距和最大宽度与抗拉强度的关系

3 结 论

(1) 从力平衡条件出发，推导了裂隙开展的间距和宽度的表达式，据此提出了开裂最大间距和宽度的概念，提出了最大间距和最大宽度的概念，可用于判定裂隙最终规模的依据。

(2) 分析了不同参数对膨胀土开裂最大间距和最大宽度的影响，认为其与土体的收缩系数、最大变湿、变形模量、抗拉强度、水平阻力系数等因素密切相关。相同条件下，变形模量越大，最大间距和最大宽度缓慢减小，但变化幅度不明显。收缩系数和最大变湿越大，最大间距迅速减小，存在极小值；而最大宽度逐渐增大，与收缩系数呈较好的线性关系。水平阻力系数越大，最大间距和最大宽度均迅速减小，存在极小值。裂隙深度和土体抗拉强度越大，最大间距和最大宽度均逐渐增大，呈现出较好线性关系。

(3) 在一定条件下，土体裂隙的最大间距存在极小值，表明当裂隙开展到一定程度时，水分的继续丧失仅导致已有裂隙的加深加宽，不会生成新的裂隙，裂隙形态基本保持稳定。