库水位波动下三峡库区典型堆积层滑坡位移特征及预测

陈玉华，邱冬冬，程志伟，詹淦基，陈俊熙

(1.福州大学 环境与资源学院， 福建 福州 350116；2.地质工程福建省高校工程研究中心， 福建 福州 350116)

堆积层滑坡是在其自身地形地貌、地质结构等内在因素基础上，受内外动力耦合作用孕育形成，其危害性往往令人触目惊心，尤以我国长江三峡库区为甚。据调查，三峡库区的数千处崩滑灾害，仅小部分开展工程治理、搬迁避让等防治措施，其余都实行监测预警。因此，堆积层滑坡位移特征及预测研究对三峡库区及相似区域滑坡预测预警、保护人民群众生命和财产安全具有重大的实用价值。

由于滑坡深部位移监测难度较大、精度较低及地表GPS监测技术的成熟，且考虑到地表监测点和滑带岩土体位移时序具有基本相同的规律特征，研究人员主要基于地表GPS位移监测信息进行滑坡位移预测及灾害预报[1-3]。目前，已有众多的滑坡位移预测模型被提出，极大了推动了滑坡位移预测及灾害预测预警研究。这些位移预测方法主要可分为4类：

(1) 依据经验的曲线拟合预测方法。该方法用数学模型对位移时序曲线进行拟合，再对时间外延进行位移预测。采用的数学模型主要有灰色模型[4-6]、马尔可夫链[7]、人工神经网络模型[8-11]等以及多种数学模型的组合预测方法[12-15]。

(2) 考虑环境变量的曲线拟合预测方法[16-19]。该方法也是用数学模型进行位移时序拟合预测，但在拟合过程中，考虑了影响滑坡稳定性的环境变量。

(3) 依据滑坡演化动力学的位移预测方法[20-21]。该方法依据滑坡演化机理进行位移预测，但由于影响滑坡稳定性的各因素耦合作用导致的非线性及复杂性，目前尚难以准确建立滑坡动力学方程。

(4) 基于数值模拟的位移预测方法[22-24]。该方法能较好地考虑主控因素作用下的滑坡演化全过程，是有良好前景的位移预测方法，但目前的模拟方法尚存在静力计算时步与真实时间难对应的问题。

由上可知，合理考虑滑坡稳定性影响因素及演化动力学过程的位移预测方法仍需要进一步研究。本文以重庆奉节县某滑坡作为三峡库区典型堆积层滑坡，基于地质及位移资料分析，总结滑坡位移特征及主控因素；提出基于库水运行工况概化，通过GeoStudio软件SEEP/W模块获取各工况下的滑坡渗流场，并将其依次导入FLAC3D数值分析平台，获取滑坡位移场的位移预测方法；最后通过计算位移与实测位移的对比分析，证实了本文方法的可行性和可靠性。

1 滑坡位移特征分析

重庆市某滑坡处于长江一级支流大溪河右侧支沟红崖沟左岸斜坡地段，行政区划隶属于重庆市奉节县鹤峰乡。该区地质构造以褶皱为主，滑坡处于巫山向斜NE翼，区内次级褶皱及裂隙发育，岩体破碎。滑坡所处地貌为中等切割低山河谷地貌，滑坡原始地形坡度约30°，坡顶与坡底高差达160 m，坡面向东北倾斜，属于斜交坡。该区域多年平均气温16.4℃，一月份平均气温5.1℃，七月份平均气温27.5℃。全年雨量丰沛，多年平均降雨量1 145 mm，月最大降雨量548.4 mm，日最大降雨量191.5 mm，降雨多集中于5月—9月。

1.1 形态及地质条件

该滑坡主轴向长度约460 m，平均宽度约250 m，滑体平均厚度35 m。滑坡现有分布面积约11.1×104m2，体积约388.5×104m3，属二级大型堆积层滑坡。滑坡右侧边界为冲沟，冲沟切割深度为50 m～80 m，左侧后部边界为山脊，前部边界为冲沟，冲沟切割深度为30 m～50 m，后缘高程290 m，为陡壁，前缘高程141 m，在三峡水库运行条件下，属于涉水滑坡。

该滑坡的滑体为第四系全新统堆积层(Qdel 4)，岩性主要为碎、块石夹粉质黏土，呈棕红色，碎石粒径一般2 cm～18 cm，呈棱角状、碎块状，在滑坡体表部可见块石最大粒径为450 cm，呈散体结构。碎、块石间的充填物为粉质黏土，含量约占30%。滑带位于第四系滑坡堆积层与基岩接触面，呈折线形，主要为粉质黏土夹碎石、角砾，碎石角砾粒径为0.5 cm～3.0 cm，黏粒含量较高，土石比约4∶1。滑床为三叠系中统巴东组(T2b)泥质粉砂岩，岩层产状348°∠36°。

该滑坡的地下水可分为第四系松散岩类孔隙水和基岩裂隙水。前者赋存于滑坡体的碎块石夹粉质粘土中，主要接受大气降水的补给，受季节变化影响明显；后者赋存于三叠系中统巴东组泥质粉砂岩裂隙中，主要接受侧向径流补给和上部孔隙水入渗及降水补给。总体而言，在三峡水库运行条件下，滑坡地下水渗流场受库水位波动影响明显，为研究该滑坡的稳定性演化特征，在滑坡体表面布置若干监测设备，其中GPS监测点2个，同时在滑坡体外布置GPS基准点2个，该滑坡的工程地质主剖面图见图1。

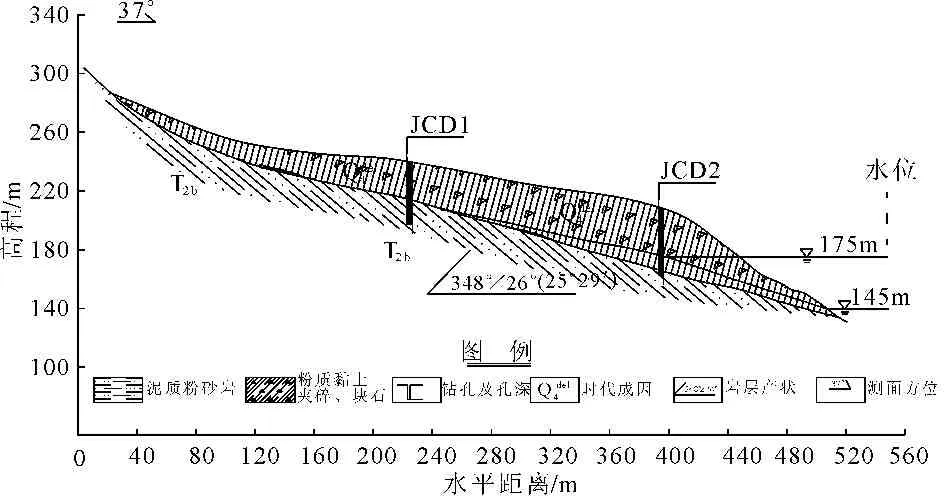
图1滑坡Ⅰ-Ⅰ′工程地质主剖面图

1.2 位移特征

三峡水库自2003年试验性蓄水以来，每年的水位调度过程基本相似且都具有“骤升缓降”的特点(见图2)，即每年的8月—11月为水位骤升段，大约历时3个月，而每年的11月至次年6月为水位缓降段，大约历时8个月。

为了准确全面地对滑坡位移特征进行研究，本次选取滑坡监测初始的约2.5个水文年作为代表性时间段(见图3)。分析该滑坡位移与库水及降雨间的相关性发现，该滑坡的位移明显增加现象并非发生在强降雨时期，而是库水位强烈波动时期。由此可知，该滑坡的主控外因是库水位波动，即在后续数值模拟研究中，忽略降雨对滑坡变形的影响是合理的。

图2 三峡库区坝前库水位变化曲线(2006年—2014年)

图3监测点总位移与库水位变化关系图

该滑坡Ⅰ-Ⅰ′主剖面的两处地表总位移数据与库水位的关系见图3。由图3可知，在库水位第1次从145 m蓄水到156 m及后续下降到145 m的过程中，两处总位移呈波动式上升，但并不明显；当第2次从145 m蓄水到172.7 m时，两处总位移都有较为明显的增加，尤其是库水位从172.7 m下降到145 m时，两处总位移增加明显，后缘JCD1监测点总位移达到107.5 mm，前缘JCD2总位移达到91.3 mm。总体而言，该滑坡变形受库水位波动影响明显，尤其是对库水位下降较为敏感。

该滑坡主剖面的两处监测点在垂直位移、水平位移、总位移及其与库水位波动的关系上，具有基本相同的规律特征。以滑坡前缘监测点JCD2为例(见图4)，随着库水位的周期性上升与下降，水平位移持续增大，总位移与水平位移具有基本同步变化的特征，表明滑坡以水平位移为主，垂直位移曲线总体呈现震荡且逐渐下沉的特征，且前期振幅在15 mm左右，当库水位从172.7 m下降到145 m过后一段时间，最大垂直位移达到近-40 mm(下降为负)，其后随着库水位上升，又有隆起的趋势，表现出了一定的滞后性。

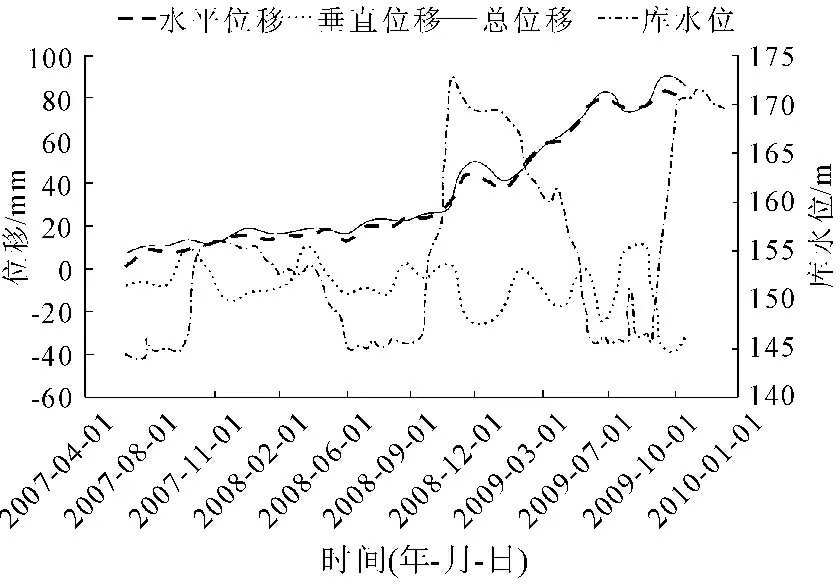
图4水平、垂直、总位移与库水位变化曲线图

2 滑坡位移预测研究

本文选取关键时间节点，开展局部时段的水-力耦合数值模拟研究，以期兼顾计算精度和计算效率。

本文提出的库水型堆积层滑坡位移预测基本步骤为：(1) 将库水位波动特征进行概化，得出合理可靠的库水位波动曲线；(2) 基于滑坡饱和-非饱和渗流计算程序，获取库水位波动关键时间节点的滑坡渗流场；(3) 将三维地下水位面并导入有限差分程序，获取滑坡位移场及监测点位移；(4) 在有限差分程序中导入新的地下水位面，进行相关位移场计算，并依此类推。

2.1 库水位波动曲线概化

基于该滑坡位移特征分析可知，其在2008年8月至2009年9月间的位移明显，因此，选取该时段作为本文滑坡位移预测研究的对象。由于实际水位调度曲线具有一定波动性，为了更方便且合理地进行数值模拟，对三峡水位调度曲线进行概化，忽略局部微小波动，最终将该时段的水位调度简化为以下8种计算工况(见表1)。

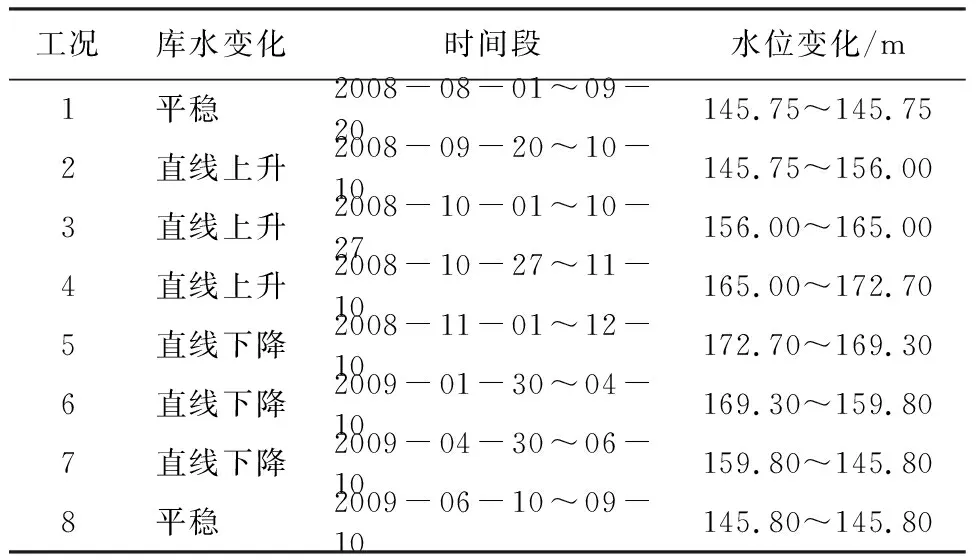
表1 数值模拟计算工况表

2.2 渗流场特征

该滑坡的滑体由碎块石土组成，为强透水介质，滑床由巴东组泥灰岩组成，为相对隔水层。因此，在滑坡渗流场计算中，可仅考虑库水对滑体内地下水位的影响。本文基于Ⅰ-Ⅰ′主剖面，利用GeoStudio软件SEEP/W模块建立渗流计算模型(见图5)。该模型共6 153个节点，5 850个单元。其中，以库水位上升稳定阶段的水位145.75 m作为初始条件，最高库水位(172.70 m)之上的坡面节点设置为零流量边界，最高库水位之下的坡面节点设为随时间变化的动水头边界(与表1对应)，滑面上的网格节点设置为零流量边界。

图5滑坡渗流计算网格模型

以Van Genuchten模型作为土-水特征曲线拟合及非饱和渗透系数估算的模型，并忽略水的体积压缩。该模型的参数基于文献[25]提出的各类型土的建议值及滑坡勘察报告测试数据进行综合确定，其取值情况见图6和图7。

通过上述建立的渗流计算网格模型、定义的渗流计算参数以及设置的初始条件和边界条件，计算得出各工况的滑坡地下水浸润线，见图8和图9。

由各工况下滑坡渗流计算结果可知：库水位上升阶段浸润线在滑坡体内呈“倒流”现象，浸润线基本为直线，且随着库水位上升速率的增大，斜率逐渐增大；在库水位下降过程中地下水浸润线呈“顺流”现象，基本呈直线状，且库水位下降速率越大的浸润线越陡。这说明滑坡地下水的补给或者排泄需要一定的时间。

图6 滑体土体积含水率与基质吸力关系图

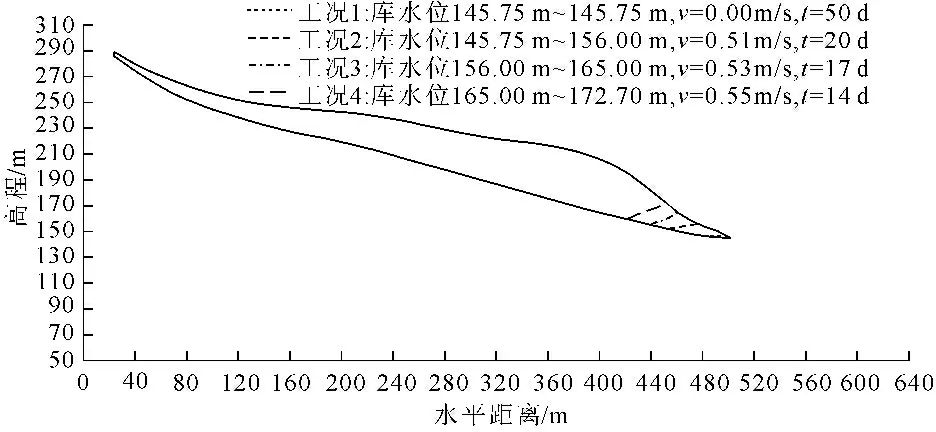
图7 滑体土渗透系数与基质吸力关系图

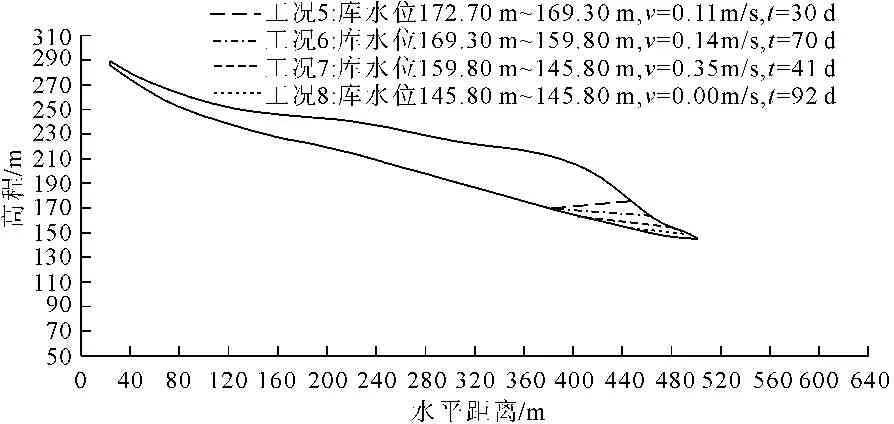
图8 库水位上升过程各计算工况下的地下水浸润线

图9库水位下降过程各计算工况下的地下水浸润线

2.3 位移场特征

本文将该滑坡的物理介质概化成滑体土与滑床基岩两种介质，基于FLAC3D数值分析平台和该滑坡的几何形态特征，构建的数值模型如图10所示。其中，滑体表面的102、100号点分别对应着JCD-1、JCD-2地表GPS监测点。

图10滑坡三维数值计算模型

基于该滑坡的勘察报告，确定出岩土体的物理力学参数如表2所示。其中，设置的碎块石土的抗拉强度不为0的原因在于：若抗拉强度为0，则在刚开始计算时就会有并在后续计算中一直存在大量的拉破坏，这与滑坡的实际变形破坏情况不符，并且，碎块石土经过压实后，具有一定的抗拉强度，这已被该滑坡及三峡库区同类滑坡取样试验所证实。

提出的水库型堆积层滑坡位移预测的关键计算过程为：首先，将工况1的主剖面处二维地下水位面拓扑拓展为整个滑体的三维地下水位面，各处滑体前缘的浸润线位置与主剖面基本一致(受库水位影响所致)，而在除主剖面外的其它滑体内部，浸润线位置主要依据与地面、滑面的相对比例关系；然后通过Water table face命令将其导入FLAC3D数值程序，生成无渗流模式下的孔隙水压力场，并在滑坡前缘施加相应的库水反压力，将该工况计算到收敛为止，无需校核时步与真实时间的关系，获取滑坡位移场及监测点位移；再将滑坡现有原有孔隙水压力场清除，应力应变信息保持不变，用相同方式导入工况2的三维地下水位面，并计算获得滑坡位移场及监测点位移；按上述方式，依次导入后续地下水浸润面进行计算，获取相应的位移场及监测点位移。由此获得不同库水位波动条件下滑坡位移特征。

表2 岩土体物理力学参数取值表

数值模拟结果表明：滑坡变形主要集中在中前部，特别是右侧中部(高程170 m～200 m)位移明显较大，且前部位移比中部位移要大，另外局部后壁也出现了较大的位移，详见图11(工况6，较危险工况)。基于上述8个工况下的数值模拟结果推断，该滑坡在库水位作用下将发生前缘蠕滑、后缘拉裂、中部剪断的三段式破坏模式。

图11工况6(169.30 m～159.80 m)下的滑坡位移云图

2.4 可靠性检验

为检验数值计算结果的可靠性，将两处地表GPS监测点的计算位移与实测位移进行对比分析(见图12和图13)，可得以下基本认识：

(1) 两处滑坡监测点的计算位移比实测位移偏小，但总体来说，计算位移与实测位移较为吻合，预测效果较好，且无需考虑计算时步和真实时间对应问题，表明本文提出的库水位波动下堆积层滑坡位移预测方法是可行、可靠的。

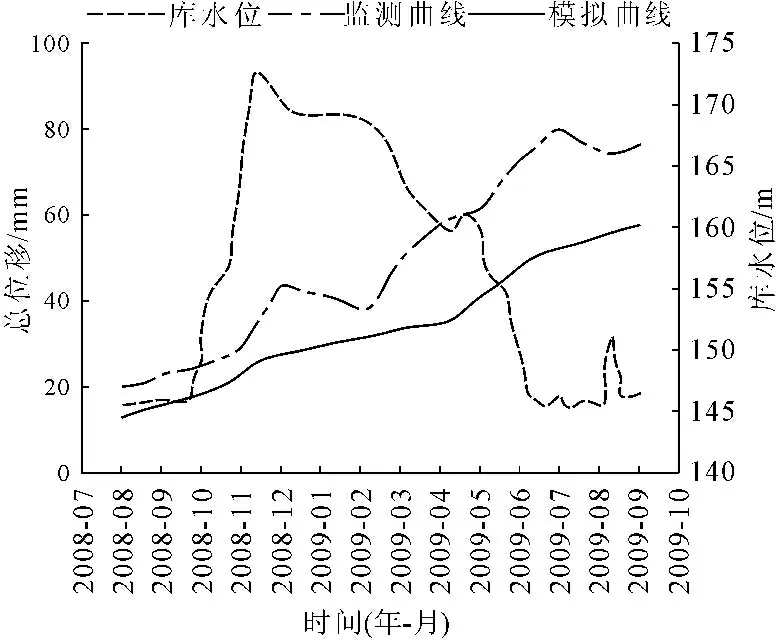
图12 JCD-2监测点计算位移与实测位移对比图

图13 JCD-1监测点计算位移与实测位移对比图

(2) JCD-2监测点实测位移与计算位移间的差异比JCD-1监测点更小，说明JCD-2监测点对库水更为敏感，位移受库水位变化影响更大，而监测点JCD-1由于受到大气降雨等其他外界干扰，导致其对库水位变化的敏感性相对较差。

(3) 在数值模拟静力计算中，对于收敛解而言，滑坡孔隙水压力场与应力场是同步进行的。而实际水库型滑坡演化过程中渗流场与应力场的耦合作用具有时间效应，实测位移波动相比库水位波动、降雨等具有一定的滞后性。这些将导致数值计算位移与实测位移难以同步变化。

3 结 论

本文以重庆市某滑坡作为典型堆积层滑坡，分析了该滑坡位移特征，基于数值模拟进行了滑坡位移预测并检验了其可靠性，主要获得了以下结论：

(1) 该滑坡以水平位移为主，总位移与水平位移具有基本同步变化的特征。该滑坡位移受库水位波动影响明显，尤其是对库水位下降较为敏感。

(2) 提出了基于库水位运行工况概化，通过GeoStudio软件SEEP/W模块获取各工况下的滑坡渗流场，并依次将其导入FLAC3D获取滑坡位移场的水库型堆积层滑坡位移预测方法。

(3) 该滑坡实测位移与计算位移不完全吻合的原因主要在于未考虑降雨等外界因素及应力场-渗流场全过程耦合作用。

(4) 受基础理论和技术手段的限制，目前准确预测滑坡位移仍无法做到，但在实际滑坡灾害预测中，除滑坡位移值本身外，滑坡位移的增量特征和规律对于滑坡灾害的预测预报同样具有重要意义。