模糊综合评判在山区公路边坡稳定性分析中的应用

陈云超，杨平庆

(安徽理工大学 土木建筑学院， 安徽 淮南 232001)

随着国家基础设施建设的迅速发展，山区新建的公路和铁路工程不断增加，特别是高速公路的大量兴建，对山区边坡工程的稳定性提出了更高的要求[1]。其中边坡稳定性评价对边坡工程设计施工起着至关重要的作用，因此边坡稳定性评价方法一直是众多岩土工作者重点研究与改进对象。文献[2]通过对大量边坡极限平衡分析资料总结对比，发现即使安全系数大于1.6，边坡依然出现破坏情况。这主要是由于传统的边坡稳定性定量分析方法如极限平衡法和数值分析等，在计算模型以及材料力学参数选取上存在假设和不确定性，而无法准确描述边坡稳定的实际情况。而边坡稳定性定性分析方法如地质分析法、工程类比法、图解法和专家系统等[3]无法提供工程建设所需要的量的依据。考虑到这些问题，近年来众多专家学者通过结合多种理论分析方法，提出了很多结合定性定量分析的边坡稳定性综合评价方法，如模糊综合评价法、灰色系统评价法、神经网络评价方法、Logistic回归分析法以及突变级数法等[4-6]。

王艳霞[7]认为将数据统计资料、知识经验等定性半定量信息采用模糊数学方法，对边坡稳定性进行综合分析，可以得到更为符合实际的结果。洪海春等[8]在充分考虑影响边坡稳定主控因素的基础上，分别建立了一级和两级模糊综合评价模型，通过对比，认为两级模型优于一级模型。张勇慧等[9]根据公路岩质边坡的特点，明确指标选取原则，结合层次分析法建立了公路岩质边坡稳定性模糊分级方法。阮航等[10]利用大量边坡样本，通过最大熵原理和工程模糊集理论，确定指标综合权重，提供一种公路边坡稳定性模糊评价的改进方法。

模糊综合评价本质是指标隶属度到目标隶属度转化过程，其重点在于权重和指标隶属度的有效性及其转化方法的合理性[11]。边坡系统在内外部因素影响作用下，对其稳定情况具有明显的非线性变化表现，而在边坡稳定性模糊综合评价模型中多采用的是线性加权模型，通过指标隶属度与权重线性组合得到最终的目标隶属度，这种方法过于简单，也与实际情况有很大偏差。本文通过分析前人研究经验，充分考虑分析影响边坡稳定性的主控因素及其对边坡系统的非线性影响特征，同时兼顾各因素指标的主客观权重取值，基于层次分析思想建立两级非线性模糊综合评价模型，并将其应用于工程实践中，对相似工程建设具有一定的指导借鉴作用。

1 评价模型

1.1 模糊综合评价法

模糊综合评价[12]是基于模糊变换原理和最大隶属度原则, 综合考虑评价目标及其特征属性的相关因素, 进而进行等级评价。

设论域U是n个被分类对象构成的集合，每个对象又有m个描述对象特征的变量。首先确定两个模糊子集：特征评价集合V，V={V1，V2，…，Vm}；评价因素集I，V={I1，I2，…，In}。由此确定n个指标对应m种评价等级的总判断矩阵R：

(1)

由(V，I，R)构成一个综合评价模型。

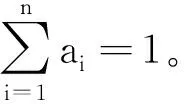
由此，可对I→V进行模糊变换，变换结果为B∶B=A∘R，记B={b1，b2，…，bm}，其中bj(j=1,2,…,m)为第j种评判Vj对应模糊集合B的隶属度。最后根据最大隶属度原则，确定目标评价等级。

1.2 非线性模糊算子

1.3 综合评价

此次针对边坡稳定性问题的复杂性、层次性，将边坡稳定性影响因素分为两级三类，边坡稳定性采用四级分类，即Ⅰ级(稳定)、Ⅱ级(基本稳定)、Ⅲ级(极限稳定)、Ⅳ级(失稳)。因此本次评价活动需进行两级模糊变换。考虑到两级指标的不同特性：(1) 对一级指标进行量化处理后，通过数学方法，可以直接描述评价对象稳定情况，但随其在不同取值范围变化，对评价结果往往呈现非线性对应关系；(2) 二级指标包含因素较为繁杂，具有很强的模糊性与不确定性。这里我们采取前文引入的非线性模糊算子对一级指标进行模糊变换，二级指标采用线性加权模型M(°，+)对其进行处理。最终根据最大隶属度原则确定边坡稳定性分级。

1.4 评价有效性识别

在实际应用中，某些条件下模糊综合评判结果会出现两个及以上隶属度分量bj相等或接近情况，这表明最大隶属度原则失效，评价不合理。因此需要对评价结果进行有效性识别[14]：

(2)

式中：β=maxbj，γ=secbj(B中第二大分量)。当1≤α<+∞时，认为最大隶属原则非常有效；当0.5≤α<1时，认为最大隶属原则比较有效；当0<α<0.5时，认为最大隶属原则最低效效；当α=0时，则认为实施最大隶属度原则完全失效。

2 评价要素分析

2.1 影响因素选取

边坡稳定性影响因素选取应遵循独立性原则，防止各因素之间存在交叉情况，以避免造成指标隶属度的“冗余值”，导致评价结果的不准确。笔者结合众多文献研究，现将各影响因素分为三类两级指标：(1)自然因素：年均降雨量C11、地下水影响C12、植被覆盖现状C13、(2)设计因素:坡高C21、坡角C22、排水条件C23、加固强度C24和(3)地质因素：岩体类型C31、风化程度C32、不利结构面影响C33、坡体结构C34、黏聚力C35、摩擦角C36。

2.2 隶属度取值原则

一般而言，根据评价指标的性质，可将其分为定性指标和定量指标。对于定量指标可采取公式法确定隶属函数，通过隶属函数确定各指标相对应的评价等级的隶属度。而由于定性指标往往只能用定性语言描述，直接求取隶属度较为困难。针对这种情况，笔者根据专家的意见，对定性指标做定量化处理，将其定性描述转化为评分分值，并根据相关文献确定不同分级标准，再由隶属函数计算出隶属度，各指标取值标准见表1。

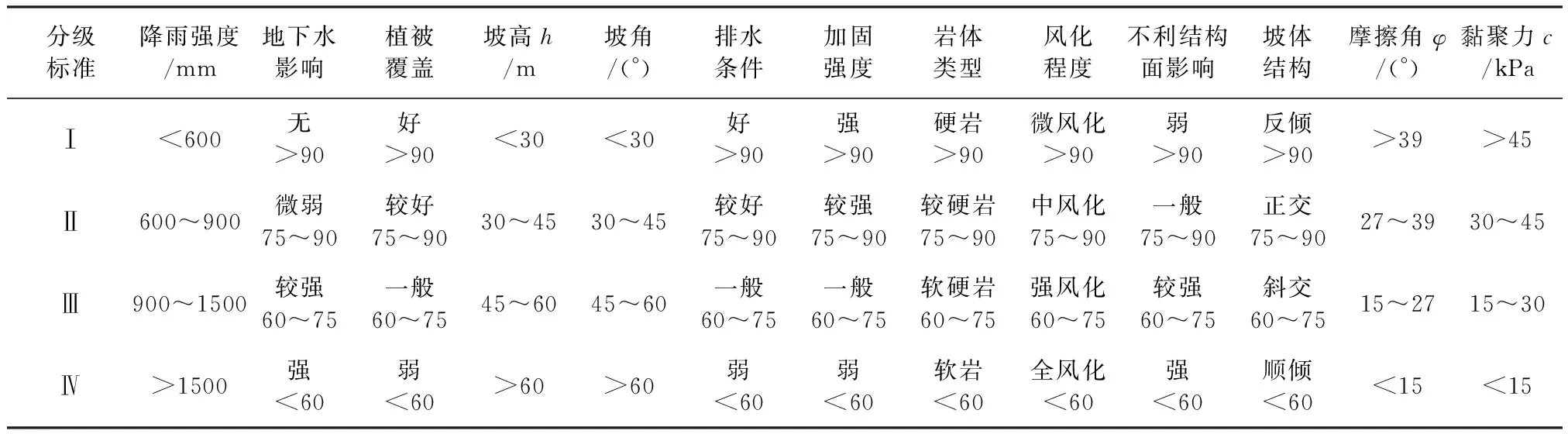
表1 指标评估取值标准

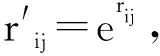
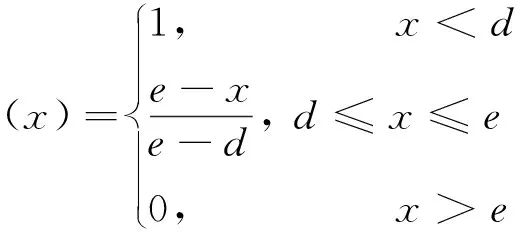
(3)

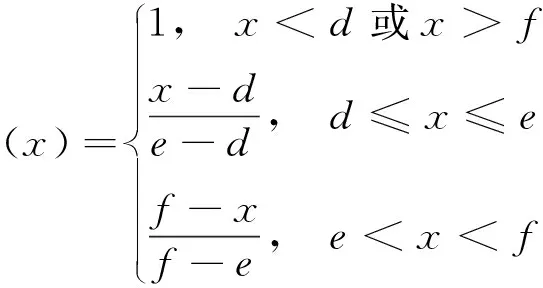
(4)

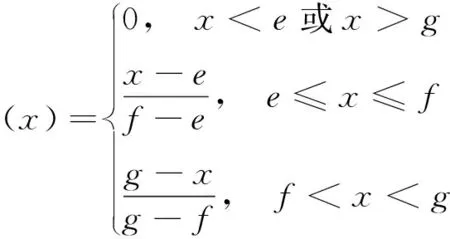
(5)

(6)

式中：x为Ⅳ指标实际取值，d、e、f、g为各等级标准取值。带入隶属函数要根据指标不同性质(成本型、效益型)作适当调整。

2.3 权重确定方法

指标权重的确定是综合评价过程中关键的部分。根据权重确定方法受主客观因素影响程度的不同，可将其分为两类:一类是主观权重确定方法,主要有专家调查法(Delphi)和层次分析法等。另一类则是依据评价指标数据变化特征来确定权重的客观权重确定方法，包括熵权法[17]、标准离差法、关联函数法等。一方面主观权重法基于专家主观判断，可以充分利用到工程实践中的经验，但又容易受专家知识经验主观差异影响，缺乏科学的判断依据。另一方面，客观权重法基于样本数据，可以弥补主观权重的不足，但又过于依赖数据值，往往容易受样本数据离散极值影响，对评价模型造成一些偏差。基于这两方面考虑，本次采用主(层次分析法)客(熵权法)观组合权重确定方法计算权重。由于熵权法依赖样本数据，不适用于中间层权重计算，因此，对于二级指标仅用层次分析法确定其权重。主要方法及步骤如下：

(1) 层次分析法计算权重：首先将各指标进行排序，根据层次分析法的1～9标度法构造判断矩阵Y。

(7)

其中，yij>0，yij=1/yji,yjj=yii=1。然后再通过判断矩阵Y求出其最大特征值λmax对应的特征向量A′，将其归一化后，即为所求主观权重向量As，并且对判断矩阵进行一致性检验。

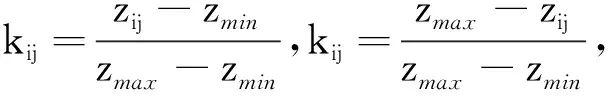
最终确定指标熵为：

(8)

由熵值求得客观权重：

(9)

(3) 将主观权重和客观权重结合起来，通过熵值变量对两者进行加权组合，最终确定综合权重[18]：

(10)

2.4 Λ确定方法

借鉴层次分析法“九标度”取值思想[19]，考虑因素指标对评价目标的突出影响程度，确定Λ的取值原则见表2。

表2 Λ取值原则

3 工程应用

河百高速公路是广西“七纵六横”高速公路主骨架网中“贺州(灵峰)至隆林(板坝)高速公路(横2)” 中的一段。线路全长177.336 km，建成后是广西境内东西向最重要公路之一。公路位于广西西北部，云贵高原台地东部边缘，横穿自西北二东南流向的红水河，地形起伏较大。沿线所经地貌不良地质十分复杂，雨季集中且降雨量大，容易发生滑坡等地质灾害，严重影响高速公路施工及运营安全。因此，此次随机选取3组边坡，采用本文构建的边坡稳定性评价方法对其进行评价分析，具体过程及结果如下文。

3.1 隶属度计算

首先对3组边坡各指标进行量化处理，结果见表3。再将其代入隶属函数中(公式(3)～公式(6))，得出相应的指标隶属，考虑篇幅限制仅以K136+500—K136+800为例，计算结果见表4。

表3 指标实测值

表4 指标隶属度

3.2 权重计算

根据层次分析法和熵权法分别计算出一级指标权重，再通过公式(10)，充分利用样本熵值对主客观权重进行加权组合，确定综合权重。二级指标涵盖内容较多，无法获取统计数据，因此二级权重仅采用层次分析法确定，主要参数及结果见表5。

表5 C11指标权重

3.3 综合评价

对于一级模糊变换，首先确定各指标突出影响程度系数，Λ1={3，2，1}，Λ2={1，3，7，5}，Λ3={3，3，5，2，3，3}，最后根据最大隶属度原则确定最终评价结果，综合评价结果见表6,且均满足最大隶属度有效原则。

3.4 结果分析

由表6评价结果可以看出，K136+500—K136+800和K49+540—K49+740边坡处于Ⅳ级不稳定状态，K144+685—K144+880边坡处于Ⅱ级稳定状态，根据长期监测以及现场勘察情况表明此次评价结果符合实际情况。

结合表3和表6还可以发现K136+500—K136+800和K49+540—K49+740边坡虽然处于Ⅱ、Ⅳ两种不同状态，但两处边坡自然条件以及地质条件较为相似，但前者排水条件要远远好于后者。因此，针对此次评价对象(河百高速沿线边坡)存在的岩土体性质较差、渗透性好、降雨集中等不利因素，笔者认为应对该类边坡坡体内外部做好排水工作，其有效性甚至高于一般的加固措施，从长远角度看对边坡的长期稳定也十分有利。

表6 非线性模型评价结果

4 结 论

(1) 本文基于模糊综合评价方法，考虑到影响因素与评价对象之间的非线性影响特征，引入非线性模糊算子，构建了边坡稳定性分析的两级非线性模糊综合评价模型，最终将其应用于河百高速沿线边坡，结果表明该方法评价结果与实际情况符合度较高。

(2) 权重的计算考虑了主客观两方面因素的影响，基于层次分析法和熵权法两种权重计算方法，并且通过熵值对两者进行加权组合，充分利用样本数据，增加了权重的科学性，进一步提高了评价模型的准确性。