岩质边坡地震动力响应研究进展

宋丹青，陈志荣，陈俊栋,3

(1.上海交通大学 船舶海洋与建筑工程学院， 上海 200030；2.中国地质科学院 水文地质环境地质研究所， 河北 石家庄 050061；3.中铁科学研究院有限公司， 四川 成都 611731)

2017年6月24日，四川省茂县新磨村发生山体滑坡，这是一起由于历史上两次大地震导致山体发生破碎，岩体完整性降低，在强降雨作用下发生的高位山体滑坡，这使地震滑坡再次引起重视。在内陆地形复杂区域，例如我国西部山区地形多样复杂，地震主要将会诱发大量的滑坡，这也成为了主要的地震灾害[1-2]。随着人类社会的发展，地震滑坡对人类的生命、财产和居住环境产生了诸多不利的影响，地震滑坡灾害日益成为影响社会稳定发展的一项重要威胁。

在国外，地震滑坡灾害严重，例如在2004年日本的新泻中越地震中，产生了大量的滑坡，宽度50 m以上的滑坡超过了360个，造成了大量人员伤亡，据不完全统计在新泻县受伤人员超过了3 000人[3]；在2008年岩手宫城内陆地震(Ms=6.9)中，诱发了超过4 000个地震滑坡，造成数十人死亡和失踪，450多人受伤[3-4]。20世纪以来，我国地震多发，震害造成的损失巨大[5]。我国地处地中海-喜马拉雅地震带和环太平洋地震带之间，这直接导致我国断裂带繁多，地震频发[6]。20世纪以来，我国地震多发，震害造成的损失巨大，我国历史上的中强震及其诱发的滑坡灾害如表1所示。尤其是，2008年汶川地震诱发了大量的滑坡和崩塌等地震灾害，包括大约56 000处滑坡和岩石崩塌，引起了超过了10 000多处潜在的地震灾害，尤其是岩石崩塌[6]。因此，在岩土工程和地震工程中地震作用下岩质边坡的动力稳定性研究已经成为一项重要课题。

针对岩质边坡地震稳定性的研究已经取得了较多的研究成果，针对岩质边坡地震动力稳定性的评价方法研究成果进行详细的概述，并对最新研究进展及其发展趋势进行分析，为地震作用下岩质边坡动力稳定性研究提供思路。

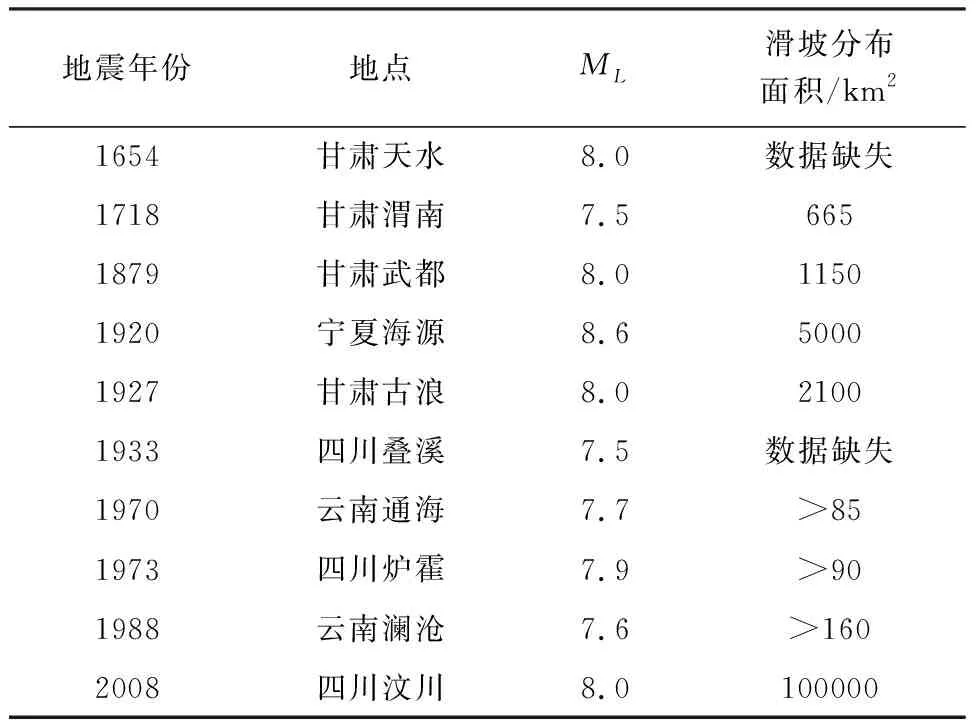
表1 我国南北地震带及邻区历史上典型ML7.5及以上大地震的地震滑坡参数统计[5，7]

1 岩质边坡稳定性计算方法研究

针对地震作用下边坡稳定性分析，目前常用的方法主要包括Newmark滑块计算方法、拟静力法、模型试验方法和数值分析方法。

1.1 拟静力法

在边坡稳定性分析中，由于简便且易操作等优点拟静力法被广泛应用于工程实践中[8]。Radoslaw等采用准静态方法，基于旋转破坏机理对边坡稳定性进行评价[9-10]。但是，由于地震力的方向及大小是随机变量，这就导致采用该方法分析地震作用下边坡的动力稳定性时存在许多限制因素。由于拟静力法时基于极限平衡理论，因此该方法与同静力条件下边坡的稳定性分析方法相似，例如瑞典法、Janbu法、Bishop法等。但是，由于不同方法计算得到的安全系数不同，这就导致在工程实践中的使用何种方法产生了任意性。朱宏伟等[11]针对这种现象，利用多种方法对边坡地震稳定性进行评价，同时对不同方法得出的结果进行对比分析，最后得出采用Janbu法应用于工程实践中分析更加准确的结论。李海波等[12]针对顺层岩质边坡，利用离散元方法分析了其动力稳定性。但是，基于拟静力方法计算的边坡稳定性与设防烈度成反比关系，因此，可以看出针对顺层岩质边坡地震稳定性评价，传统的拟静力法并不完全适用[9]。这表明，拟静力法并不是适用于所有的边坡稳定性分析。针对的地震作用下边坡稳定性评价，拟静力法未考虑地震的振动次数、频率和持时等特性，同时也未充分考虑边坡内岩土体的动力特性等，由此可知，针对边坡地震稳定性方面的研究，拟静力方法仍需要完善和探索。

1.2 Newmark滑块分析法

屈服地震强度系数是Newmark滑块分析法中最重要的参数。而在边坡稳定性计算中未将动孔压考虑进去，这将造成在整个稳定性计算中屈服地震强度系数是恒定的。为此，黄建梁等[13]为使Newmark法更加合理，对其进行改进，将Sarma假定引入边坡地震安全系数计算中，得到了动孔压，这将使边坡动力稳定性评价更加可靠。刘忠玉等[14]针对黄土地震动力稳定性进行了分析，着重研究了孔压在饱和黄土内的变化规律，得出了地震安全系数与孔压成反比的关系，相对于常规Newmark方法，得出的结果较大。吕汉川等[15]将地震动力反应与拟静力极限平衡法相结合，采用Newmark法分析了堆积体边坡的动力响应特征。陈训龙等[16]针对顺层岩质边坡，将MATLAB/Simulink工具与Newmark法相结合，提出了一种新的稳定性评价方法。Kramer等[17]对常规的Newmark方法进行了修正，认为边坡的动力响应与其潜在的滑移面上的永久位移及材料具有密切关系，而常规的Newmark方法未将这些因素考虑进去。Wang等[18]基于振动台试验采用Newmark方法结合观测表面位移，对边坡的动力响应特征进行了分析，结果表明，Newmark方法得到的永久位移与观测位移的分析结果相吻合。李红军等[19]基于平均屈服加速度，提出了Newmark滑移分析法，提高了该方法的可靠性及精确度。程小杰等[20]基于Newmark累积位移法，将引入震源方位角及边坡坡向角引入黄土滑坡评价中，将会提高小区域黄土滑坡危险性评价的精确性。董建华等[21]提出永久位移由地震过程中及地震后两部分位移组成，并且基于功能原理提出了地震后的永久位移计算模型，对基于Newmark法进行修正。

综上所述，针对地震过程中的永久位移，Newmark方法进行了充分考虑，但是，未充分考虑地震后的位移，这将在很大程度上导致计算结果的不可靠性。同时，简化了地震过程中许多计算条件，将会造成采用该方法计算结果的不可靠性。许多学者针对Newmark滑块分析法进行了改进，但是针对永久位移的计算分析，仍有待进一步改进。

1.3 数值计算方法

自1980年以来，大量的数值计算方法被用于研究岩质边坡稳定性。例如块体非连续变形分析方法(DDA)、数值流形方法(NNM)，刚体有限元方法及断裂力学有限元法等改进的有限元方法等。此外，岩质边坡稳定性研究中还有将地质学科及其他学科的新思路新方法引入进来，例如系统科学、可靠度分析、灰色系统、模糊数学方法等，这为岩质边坡稳定性的研究提供了新方法和途径。

言志信等[22]针对顺层岩质边坡，利用FLAC研究了边坡的地震动力稳定性，探讨了地震波输入持时、频率、幅值等对边坡动力响应特征的影响。刘蕾等[23]采用FLAC/PFC2D软件，建立含有非贯通层面和正交次级节理的逆层岩质边坡FLAC/PFC2D耦合计算模型，进行地震动力破坏过程模拟，研究了逆层岩质边坡地震动力破坏机理。孙东亚等[24]采用DDA模拟了以极限平衡法为理论基础的边坡倾倒分析方法，结果表明在倾倒过程中，岩体的变形具有滑移及倾倒两种状态。王举等[25]以汶川地震为例，利用UDEC数值模拟，对地震荷载作用下含节理面岩质边坡滑移、拉裂破坏的过程进行了研究。

目前，岩质边坡稳定性计算方法主要包括：有限元法、离散元法、边界元法、有限差分法、不连续变形分析方法、数值流形法等[26-28]。有限元法主要采用ANSYS、ABAQUS、RFPA等，其基本原理主要是将岩土体看做连续介质，基于离散化建立近似函数将有界区域内的无线问题进行简化，将其简化为有限元问题，进行岩土体的应力应变分析。有限元法基本上适用于所有领域，但是，也具有局限性，不适用于大变形、不连续岩体、无限域和应力集中等问题。离散元法主要采用UDEC2D、UDEC3D等，将非连续介质离散为多边体，使块体之间无变形协调约束，只满足平衡方程，允许刚体或可变形体间的位移，物体变形可以为非连续。离散元方法主要适用于求解非连续介质大变形问题，目前主要应用于被结构面切割的节理化或破碎结构的岩体变形及破坏过程方面的研究。有限差分法[29]主要采用FLAC2D、FLAC3D件，将基本方程及边界条件下的微分方程转化为代数方程进行计算，基于有限差分原理，可以有限地模拟随时间演化的非线性的大变形力学过程，主要适用于求解非连续介质大变形问题，但是具有局限性，其计算边界和单元网格的划分具有很大的随意性。不连续变形分析法[30]常用软件为DDA，采用块体元来模拟被非连续面切割的块体系统，主要用于模拟岩体的张开、移动、闭合等运动过程，对岩体的局部及整体的稳定性进行评判，但是，在针对参数选择方面具有局限性。由此可知，采用数值计算方法进行边坡稳定性评判时，由于参数选取、网格划分、边界条件及某些不合理的假设，这导致用于边坡稳定性评判时具有较多的局限性。

1.4 能量分析法

目前，基于能量分析方法进行损伤识别研究主要用于结构工程中。但是，随着边坡地震稳定性研究的深入，能量分析方法开始被引入到边坡地震稳定性研究中。能量分析方法成为了边坡动力稳定性研究的一种发展趋势。基于能量分析方法的边坡动力稳定性常用方法主要包括Hilbert-Huang变换(HHT)、小波分析方法、时序模型方法、基于模型修正的损伤识别方法、神经网络识别方法等。

基于力学平衡理论可以用于边坡动力稳定性评价，但是，并不适用于边坡产生大变形的情形中。Kokusho等[31]为此提出了一种能量方法，该方法基于刚性块体模型，在较大的地震能量作用下也不会使边坡发生较大的滑动破坏，同时，基于能量方法提出了等效摩擦系数，为研究地震稳定性问题提供了新思路。Fan等[32]基于HHT边际谱理论从能量的传播特征角度，分析了地震作用下岩质边坡的震害损伤特征及发展过程。王秀英等[33]采用Arias强度，考虑了地震时间-频率-幅值三个特性，对地震作用下边坡的动力稳定性进行了评价，结果表明采用Arias强度从能量角度对其动力稳定性进行定量分析具有推动作用。徐光兴等[34]基于能量守恒原理，建立了针对地震过程中评价滑坡动力稳定性的能量反应方程，研究了地震作用下滑坡体系中能量的转化、传递及耗散过程，基于能量法推导了的边坡永久位移计算公式。

基于实测信号的损伤识别技术可以直接针对边坡的损伤位置进行评价，同时可以对震害损伤发展过程进行分析，它不需要建立有限元模型进行分析，对传感器布设方位及位置具有较高要求。在实际过程中，如果需要对边坡震害损伤程度及位置进行判识，需要与实际监测数据结合起来进行分析。基于动力的损伤识别方法容易在工程中实施，目前震害损伤判识方法已经在结构工程中得到了广泛应用，但是，目前损伤识别技术并未在岩土工程中得到广泛应用。尤其是汶川地震以后，大量边坡存在不同程度的震害损伤，在外界诱发因素下(例如地震及降雨作用下等)将会出现大量的滑坡、崩塌和泥石流等次生地震灾害。因此，对于边坡的震害损伤识别方法的研究急需进行研究，但是，目前针对这方面的研究还处于探索阶段。

1.5 模型试验方法

振动台试验是实验室模拟地震的重要方法之一，由于振动台试验可以较真实地模拟地面运动及其对建筑物的影响作用，因此，振动台试验可以较好地用于研究地震动破坏机理及其破坏模式研究，也可以较好地评价结构的整体性抗震动力，在地震工程研究中得到了广泛应用。

Che[35]基于有限元动力分析和大型振动台试验对含不连续节理岩质边坡的地震动力响应规律及其破坏机制进行了分析。Fan等[32]基于大型振动台试验，研究了含不同软弱结构面岩质边坡的地震稳定性及其破坏机制。Liu等[36]针对含有软弱结构面的岩质边坡采用振动台试验，研究了地形效应及地质效应对地震作用下岩质边坡地震动力响应规律的影响。Huang等[37]采用振动台试验，建立硬岩和软岩两种不同岩性的岩质边坡模型，研究了两种边坡的动力响应规律。Lin等[38]通过大型振动台试验，针对加固后的堤岸边破进行试验，研究了地震作用下不同加固方案对边坡动力特性的影响。针对不同岩性的边坡，Massey等[39]基于大型振动台试验，探讨了岩质边坡的动力稳定性，对比了不同地质材料条件下的动力稳定性变化。Song等[40]基于大型振动台试验研究了含不连续结构面岩质边坡的动力响应规律。

王思敬等[41]基于振动模拟试验，研究了地震作用下岩质边坡动力稳定性问题。许强[42]通过采用大型振动台试验，针对含有水平层状上软下硬和上硬下软两种不同岩性组合的岩质边坡进行了大型振动台试验，研究了两种岩质边坡的动力特性。孔宪京等[43]利用振动台试验，针对加筋土与边坡地震稳定性的关系进行了分析，同时分析了加筋密度及长度对边坡动力稳定性的影响。董金玉等[44]基于大型振动台试验，通过建立顺层边坡模型研究了地震作用下岩质边坡动力响应规律。叶海林等[45]基于大型振动台模型试验，通过使输入地震波幅值逐级增加，研究了边坡动力破坏特征。宋波等[46]基于振动台试验好砂质边坡的有限元分析模型研究了地下水上升与边坡地震动力响应及边坡破坏模式的关系。杨国香等[47]基于振动台试验，针对不同地质构造岩质边坡进行了研究，分析了地震动输入参数对岩质边坡的动力稳定性的影响。针对层状边坡，范刚等[48]采用大型振动台试验，研究了层状边坡动力稳定性，并基于实测数据分析了岩质边坡动力稳定性的影响因素。

综上所述，大型振动台试验作为一种研究地震作用下边坡动力响应规律已被广大学者广泛使用，大型振动台模型试验已经成为一种有效、可靠的研究方法。但是，由于岩质边坡岩体结构和动力问题的复杂性，利用振动台试验研究边坡动力稳定性具有一定的局限性，例如振动台试验具有尺寸效应、难以分析地震波场的在边坡内部的传播特性等。因此，针对复杂地质构造岩质边坡利用大型振动台试验分析其动力问题的研究还需不断发展和完善。

1.6 岩质边坡动力响应特征研究进展

目前，针对岩质边坡动力响应特征的主要集中于含不连续节理边坡、含软弱结构面边坡等复杂地质构造岩质边坡，以下针对对不同类型边坡的动力响应规律进行简要介绍。

针对均质边坡、含不连续节理边坡的动力响应规律，Che等[35]采用数值计算方法进行了有限元动力计算，计算结果表明，在坡体内部或坡体表面加速度放大系数随着高程增加而逐渐增加，相比之下均质边坡的放大系数最小，含顺向及反倾不连续节理岩质边坡的放大系数最大，顺向不连续节理边坡及逆向不连续节理边坡放大系数相近。Song等[40]利用大型振动台试验分析了含不连续结构面岩质边坡的动力响应规律，结果表明(见图1)：边坡地震动力响应具有典型的地质效应及地形效应，高程、坡面及结构面具有放大效应。Fan等[32]利用振动台试验对比分析了顺向及反倾边坡的动力响应规律，结果表明(见图2和图3)：顺向边坡的放大系数相对于反倾边坡较大。目前，针对复杂地质构造岩质边坡的动力响应规律越来越多，但是由于其地质构造复杂性，其动力响应规律仍需进一步研究。

图1 含不连续结构面岩质边坡放大系数变化规律

图2 顺向岩质边坡放大系数变化规律

图3反倾岩质边坡放大系数变化规律

2 结论及展望

目前，针对岩质边坡地震稳定性评价的常用方法主要包括Newmark滑块计算方法、拟静力法、模型试验方法和数值分析方法。拟静力法及Newmark方法在评价岩质边坡动力稳定性方面具有一定的局限性。拟静力法未考虑地震的振动次数、频率和持时等特性，同时也未考虑岩土体的材料的动力性质。Newmark方法简化了许多计算条件，同时未将震后岩土体的永久位移考虑进去，仅考虑了地震中的永久位移，这将使Newmark方法的计算结果存在较大程度的不可靠性。数值计算方法及室内模型试验方法是研究地震作用下岩质边坡动力响应特征的两种重要手段，但是，单一的研究方法的可信度不如多手段研究方法高，其研究范围也不如多手段广，这是由单一方法的局限性决定的。例如，数值计算方法虽具有可操作性强、重复性高等特点，但是由于其自身局限性，对于复杂构造边坡计算将会发生不收敛现象，或对计算过程中的一些条件进行简化，模型介质本构模型不完善等缺陷，这会对计算结果的可信度造成影响。模型试验也具有尺寸效应和重力失真效应，难以模拟真实地震波等缺点，同时由于模型试验成本高，操作复杂和不可重复等缺点，难以对多类型岩质边坡进行试验。未来多种研究方法相结合的研究手段将成为一种发展趋势，这将会在很大程度上避免某一种方法计算结果带来的局限性，提高计算结果的可靠性及准确性。

针对复杂地质构造岩质边坡地震稳定性方面的研究仍需进一步深入探讨。尤其是含软弱结构面岩质边坡是一种常见的地质体，在静力作用下的受力特征、稳定性判识方法等方面的研究取得了较多的研究成果。但是，地震作用下复杂地质构造岩质边坡动力响应特征、破坏机制及稳定性判别方法还需要进一步研究。针对复杂地质构造岩质边坡地震动力响应特征及其动力稳定性评价，主要存在如下问题：

(1) 目前许多学者对地震作用下岩质边坡的动力响应特征进行了研究，但是已有的研究成果不够深入，尚需进一步深入研究，针对复杂地质构造岩质边坡的研究较少，尤其是对同时含顺向及逆向软弱结构面的岩质边坡研究更少，急需开展该类型边坡的地震响应特征及其变形破坏机制研究。目前，针对地震作用下岩质边坡响应规律的研究及对地形效应的认识，多是关于边坡顶部放大及坡底衰减，对边坡的整个坡面上及坡体内部的作用效应认识具有局限性，还未形成定量规律，尤其是对于含软弱结构面的岩质边坡难以指导抗震设计。

(2) 针对库水作用下的岩质边坡稳定性研究，在静力方面已经取得很多研究成果，但是，目前针对库水作用下复杂地质构造岩质边坡地震响应特征的研究尚无文献进行研究，尤其是库时骤降对边坡稳定性较为不利已经成为了共识，但是，库水骤降及地震作用两个不利因素联合作用下，复杂地质构造岩质边坡的动力稳定性及其破坏演化过程还需要深入探讨。

(3) 目前，研究岩质边坡地震动力响应特征大多是在时间域进行研究，已有一些文献研究了时间域的岩质边坡的加速度响应和位移响应，但是，针对时间域内的研究最终要归结到频率域进行分析。但是，针对频率域的边坡动力响应规律方面的研究较少，特别是对于含软弱结构面岩质边坡的研究更少，因此，针对频率域的库水及地震作用下含软弱结构面的岩质边坡的地震响应特征应进一步研究，在频率域研究地震动输入参数、地形效应(高程、坡体地形)、地质效应(软弱结构面)和库水骤降对其地震响应特征的影响，在频率域进一步揭示其动力响应规律。

(4) 岩质边坡因具有不连续节理、软弱结构面、层面等，致使其地震动力特性研究更加复杂，地震在软弱结构面等具有反射和折射现象，使能量发生重新分布，这一作用对岩质边坡的动力响应特征的影响是目前急需研究的一项重要课题。软弱结构面对岩质边坡的受力特征及其动力稳定性具有重要影响，尤其是具有双向软弱结构面时的影响更加复杂，针对不同类型软弱结构面对岩质边坡的地震响应特征及其稳定性的影响规律尚需进一步研究。通常认为具有反倾结构面时边坡的地震稳定性较好，但是，针对均质，含反倾结构面、含顺向结构面和含双向结构面四种类型的边坡的地震动力响应特征的差异尚不明确。

(5) 采用能量方法对地震过程中工程结构的损伤评价已经有了许多研究成果，判识方法已经日趋成熟。但是，基于能量的震害损伤识别方法在岩质边坡中的应用仍处于探索阶段，尤其是针对含双向软弱结构面的岩质边坡尚未进行研究。此外，在地震过程中仅依靠边坡失稳的破坏现象，或通过观察实验过程中的破坏现象只能定性分析边坡的破坏损伤过程。目前，采用数值计算方法虽然可以模拟地震破坏的失稳过程，但是缺乏室内试验验证，其模拟结果缺乏可信度，因此，针对这一问题仍需建立一种可以判别含软弱结构面岩质边坡震害损伤方法，并且和试验结果相对应进行验证。

(6) 目前，针对地震作用下边坡的稳定性评价方法，拟静力法仅能考虑地震波的峰值，滑块分析法仅能考虑地震波时间域特性，数值计算方法在计算过程中不得不对某些条件进行简化，或是由于边坡地质构造过于复杂而使计算结果不收敛，模型试验由于成本高、操作复杂而具有较高的推广难度。因此，针对地震波的时间-频率-幅值特性，急需建立一种可以考虑其特性的岩质边坡稳定性评价方法。含软弱结构面岩质边坡的地震响应特征、结构特征影响、震害损伤识别及地震稳定性判识方法是研究岩土领域的一个前沿性课题。缺少多手段研究，数值计算可以做到试验难以完成是复杂工作，试验可以验证数值计算，还可以更加真实地反映破坏情况，最终需要在理论上揭示机理。