基于梅尔倒谱系数的矿山复杂微震信号自动识别分类方法*

何正祥，彭平安，廖智勤

(中南大学 资源与安全工程学院，湖南 长沙 410083)

0 引言

微震监测技术是矿山生产活动过程中地压安全监测分析重要的技术环节[1-2]。微震监测系统通过将其监测区域内的各类微震信号进行实时拾取，并分析岩体破裂活动来判断岩体状态。实际采矿生产过程中，微震信号存在着多种类型[3]，如岩体破裂、爆破振动、电磁噪声和机械钻凿等。传统的人工分类处理效率较低且经常由于各种干扰导致识别错误。因此，如何快速准确地识别不同的信号类型是实现微震监测系统实时化、智能化的重要环节。

在目前用于微震信号识别分类的方法中，主要应用选取波形的相关计算的指标作为数据参数构建识别模型，如Vallejos和董陇军等[4-5]通过分析波形和事件选取得到的若干个参数作为识别指标构建了识别模型。这类方法具有一定的识别效果，但是参数的选取人为因素较高，属于非稳定参数。对微震信号进行时频分析技术总结其特征，如曹安业、陆菜平等[6-7]利用时频分析从信号的频谱特性进行总结，得出岩体破裂信号有较快的衰减速度、较发育的尾波、震幅大和较窄的频带分布等重要特征，但是该方法仅仅为人工识别提供了有效的辅助手段，无法实现信号的自动识别分类。另外，小波分析对波形更加细致的处理为微震信号的识别分类提供了新的思路，如郭涛、唐礼忠、赵国彦、朱权洁等[8-11]利用小波变换对微震信号进行了更深层次的分解，用以对微震信号进行识别，但是小波分析的方法仍然存在着小波基的选取、分解后的特征参数选择等方面的问题需要解决。

上述研究做了大量的分析探讨，并取得了较多成果，但是仍然在微震高效识别分类上存在一定缺陷。本文利用梅尔倒谱系数法提取微震信号的特征参量，结合混合高斯隐马尔可夫模型作为识别分类模型，实现了对4类常见的矿山复杂微震信号的初步识别。该方法具有较高的识别准确率和自动化程度，为实现微震信号自动识别提供了新的方法。

1 基于梅尔倒谱系数的特征提取

1.1 梅尔倒谱系数

Davis和 Mermelstein首先提出了梅尔倒谱系数，是对信号波形的短时能量谱的一种表示，是将微震信号的对数功率谱通过线性余弦变换运算投影至非线性梅尔标度中所得[12]。梅尔标度与频率的转换关系如式(1)所示：

(1)

式中：f为信号的频率，Hz。

梅尔倒谱系数对信号的失真有很好的补偿能力[13]。

1.2 梅尔倒谱系数提取过程

梅尔倒谱系数参数的提取方法[14-15]如下：

1)高通滤波：将微震信号波形通过高通滤波器可以有效地增强高频部分，使信号波形的频谱起伏减小，使得高低频的任意的频带都可以基于近似的信噪比求频谱。

2)波形分帧：每隔N个采样点将微震信号波形分段，形成新的波形单位，称为帧。根据特征提取的要求和信号的长度一般在256或512中选取N值，同时，使每帧的前后帧都与其有一小部分交叉，目的是为了避免连续的帧之间的变化过大。

3)加汉明窗：为了增加微震信号波形分帧后每一帧与相邻帧的连续性，让波形的每一帧与汉明窗相乘。假设微震信号为S(n),n=0,1,…,N-1，乘以汉明窗后则有：

(2)

式中：N为微震信号分帧后的帧数，0≤n≤N-1。

4)快速傅里叶变换：能量分布的不同，可以表示不同信号的特性，因此将微震信号转换成频域上的能量谱进行对比。在将微震信号进行连续重叠分帧后，对分解后的每一信号帧作快速傅里叶变换，借以计算频率域上的能量谱。

5)三角带通滤波器：利用一系列的三角带通滤波器在梅尔标度上转换快速傅里叶计算得到的能量谱，得到1组系数。该系列滤波器为一系列的三角窗，均匀重叠地排列在梅尔频率轴上。

6)计算对数能量谱：对每个滤波器组进行计算，并对结果取对数，得到的值为其对数能量，即可得到相应频带的对数功率谱，计算公式如下：

(3)

式中：s(m)为对数能量；X(k)为微震信号能量谱；Hm(k)为滤波器组，其中m=1,2,…,M，M为滤波器的个数。

7)离散余弦变换：利用离散余弦变换把频谱变换到时域上，所得结果就是标准的梅尔频率倒谱系数。倒谱系数的数学计算公式为：

(4)

式中：n为计算的帧数，0≤n≤N；m为梅尔倒谱系数个数，0≤m≤M,M取12。

在实际用于识别分类时，为了改善识别效果，显示梅尔倒谱系数在时间轴上的变化，将12个特征参数加上差量倒谱参数产生24维的特征参数向量。经过差分运算得到的差量倒谱参数显示了原有的12个梅尔倒谱系数在时间域上的变化。差量倒谱参数Dt(n)的计算方法如式(5)所示：

(5)

式中：C(n)为信号第n帧计算出的梅尔倒谱系数；Dt(n)为第t个一阶差量倒谱参数；为式中一阶导数的时间差，一般取=2, 1≤θ≤Θ 。

根据上述流程，可以从原始的复杂微震信号中成功提取出24维特征参数向量。

2 微震信号的自动识别分类

2.1 自动识别方法

实现信号的自动识别分类，基本方法是通过算法提取出波形的特征，利用这些特征结合机器学习实现自动识别分类。本文使用梅尔倒谱系数法从微震波形中提取出24维的特征向量，并且使用混合高斯隐马尔可夫模型实现对微震信号的自动识别分类。

隐马尔可夫模型(Hidden Markov Model, HMM)是关于时序的概率模型[16]。1个HMM通常可以由5个参数表示：λ=(N,M,π,A,B)，其中，N为HMM中马尔可夫状态链的大小，实际使用中该值为固定值。设N个状态为θ1,θ2,…,θN，则n时刻的状态为qn，qn∈(θ1,θ2,…,θN)。M为马尔可夫状态链中与每个状态可能相对应的观察值数。设M个观察值为V1,V2,…,VM，则n时刻的观察值为on，on∈(V1,V2,…,VM)。π为初始状态概率分布，π∈(π1,π2,…,πN)，其中πi=P(q1=θi), 1 ≤i≤N。参数A为状态转移概率矩阵:A= [aij]N×N，其中aij=P(qn+k=θj|qn=θi)，1 ≤i,j≤N，表示在任意时刻n，若状态为θi，则在下一时刻状态为θj的概率。B为观察值概率矩阵:B=[bij]N×M，其中bij=P(on=Vk|qn=θi)，1≤I≤N, 1≤j≤M，表示在任何时刻n，状态为θi时观测值Vk被获取的概率。

而为了更好地对复杂微震信号进行识别，混合高斯隐马尔可夫模型在原有的隐马尔可夫模型的技术上对观察值概率密度函数利用混合高斯模型进行建模，将bjk修改为当前状态和观察值之间的高斯分布概率密度函数，即：

(6)

式中：μjm为均值；Ujm为方差；cjm为高斯分布权重。构成了混合高斯隐马尔可夫模型。

2.2 微震信号自动识别分类流程

基于梅尔倒谱系数的微震信号自动识别分类主要分为3个步骤：

1)微震信号的特征提取。本文根据1.2节中的提取过程，将微震信号进行分帧，并计算每帧的梅尔倒谱系数，得到12个梅尔倒谱系数值，再通过对此12个梅尔倒谱系数值做差分计算。故1个微震信号可以提取出1个24维的特征向量，该特征向量是自动识别的数据基础。

2)自动识别分类模型的训练。选取一定时间段已标记的微震信号通过梅尔倒谱法提取特征向量，并按照类别将该特征向量作为对应事件类型训练集数据，依次得到4个训练集。作为混合高斯隐马尔可夫模型的输入数据，通过迭代求出相应的4组不同的模型参数N,M,π,A,B。每组模型参数构建的混合高斯隐马尔可夫模型即为对应微震事件类型的识别模型。微震信号特征提取及识别模型训练流程如图1所示。

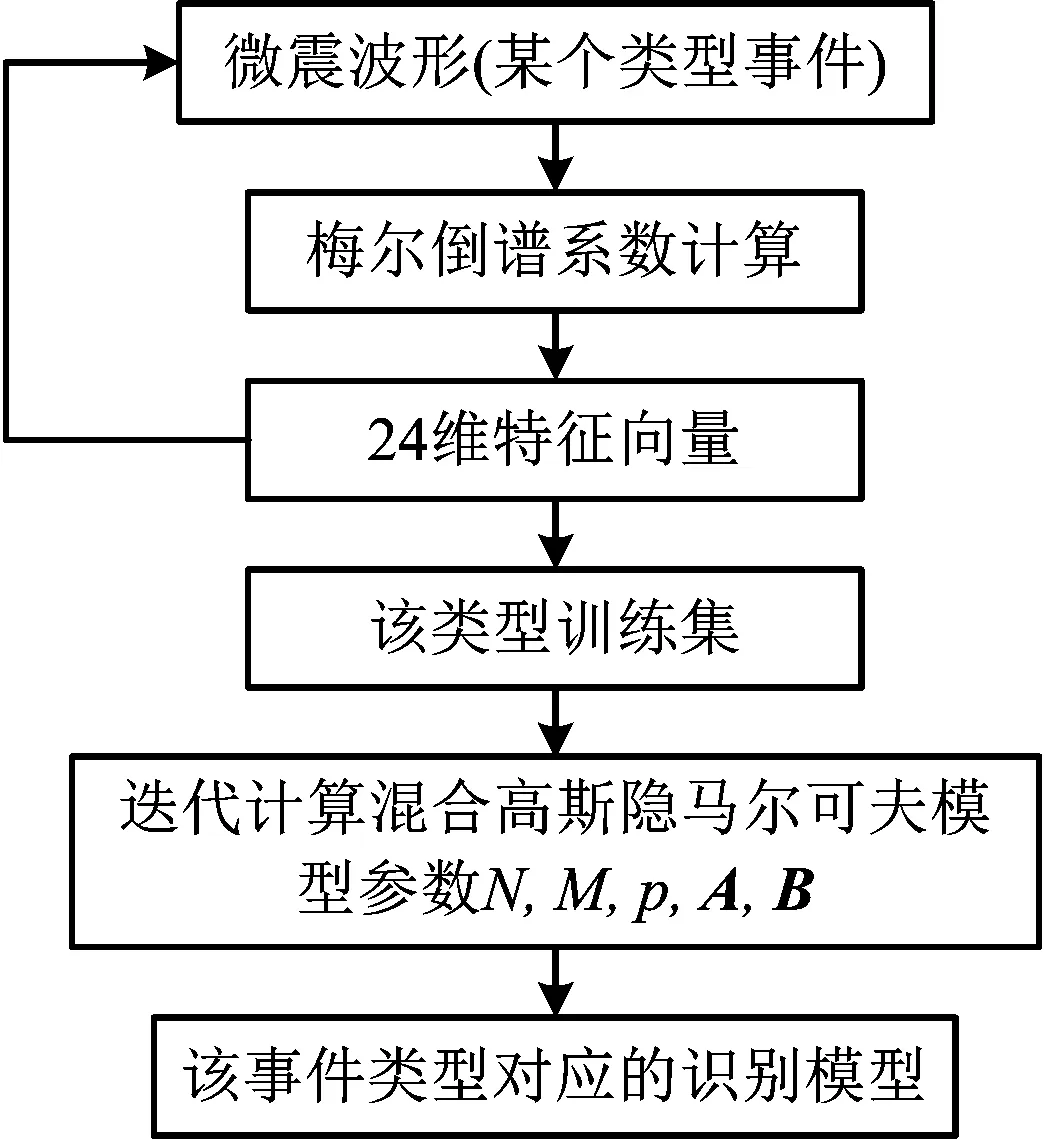
图1 微震信号特征提取及识别模型训练流程Fig.1 Process of feature extraction and recognition model training of microseismic signal

3)基于识别模型的微震事件识别分类应用。根据训练得到的4种微震事件(岩体破裂、爆破振动、钻机凿岩和电磁干扰)识别模型，对该矿山生产活动中产生的微震事件做梅尔倒谱系数计算，将得到的特征向量分别代入4种微震识别模型中计算相应的混合高斯隐马尔可夫模型概率值，取概率值最大的模型对应的事件类型，作为待判断微震事件的类型，以此实现生产活动中微震信号的自动识别分类。其自动识别分类流程如图2所示。

3 微震信号自动识别分类应用

3.1 冬瓜山铜矿微震监测系统

冬瓜山铜矿位于铜陵市以东处, 矿床处于狮子山铜矿区的深部,是我国首座开采深度达到千米并具有明显岩爆倾向性的硬岩金属矿山。冬瓜山铜矿具有矿床储量较大、埋藏深度较高的赋存特点，设计开采模式为高产强化开采，该方法的特点为开采盘区和采场较多，这导致了采场的分布范围广泛，并且多采场并行开采的模式也导致了推进速度过快，岩爆事件过多，且大范围分布。因此，引入微震监测为该矿山开采过程中的岩爆活动进行预测预警，2005年 8月28日冬瓜山铜矿正式运行微震监测系统，该系统对冬瓜山生产活动进行实时监测，并在监测数据的基础上对微震活动做了大量的研究[17]。

3.2 基于冬瓜山铜矿微震数据的识别模型训练

选取冬瓜山铜矿2017年6月1日-2017年12月13日之间的部分微震数据作为训练集，选取已人工标记的岩体破裂事件、爆破振动事件、钻机凿岩事件和电磁干扰事件各350件，共计1 400件微震事件，用以训练识别分类模型。

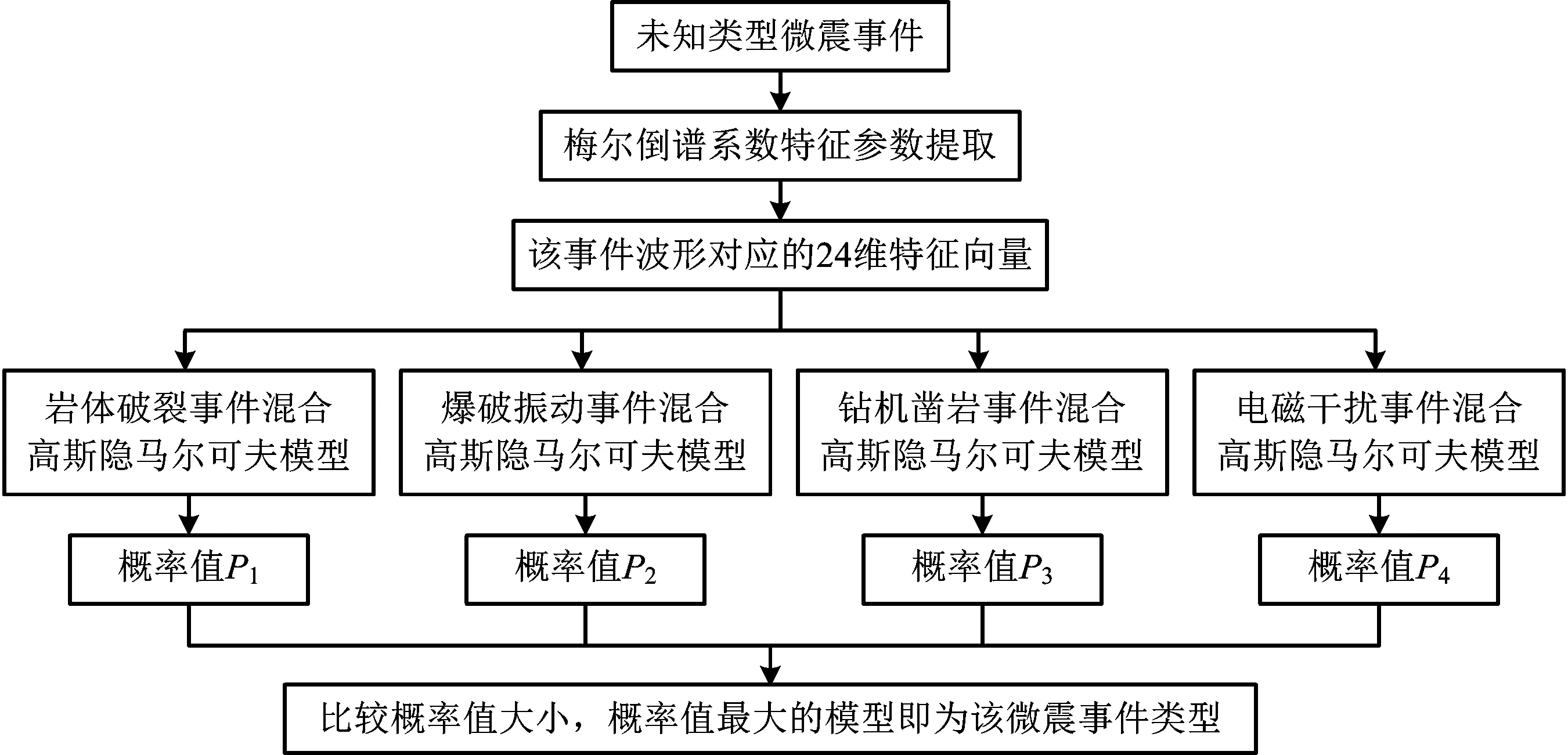
图2 微震信号自动识别分类流程Fig.2 Automatic identification and classification of microseismic signals

根据图1所示流程对选取的数据进行模型训练。首先，对每个事件波形进行梅尔倒谱系数提取，图3～6为从每种事件类型中随机选取1个事件的波形及其梅尔倒谱系数值；然后，将手动标记的事件类型与梅尔倒谱系数值组成的24维特征向量作为输入数据，确定混合高斯隐马尔科夫模型参数N,M,π,A,B；最后，通过迭代算法得出模型的最优参数，即为训练完毕的微震信号自动识别分类模型。

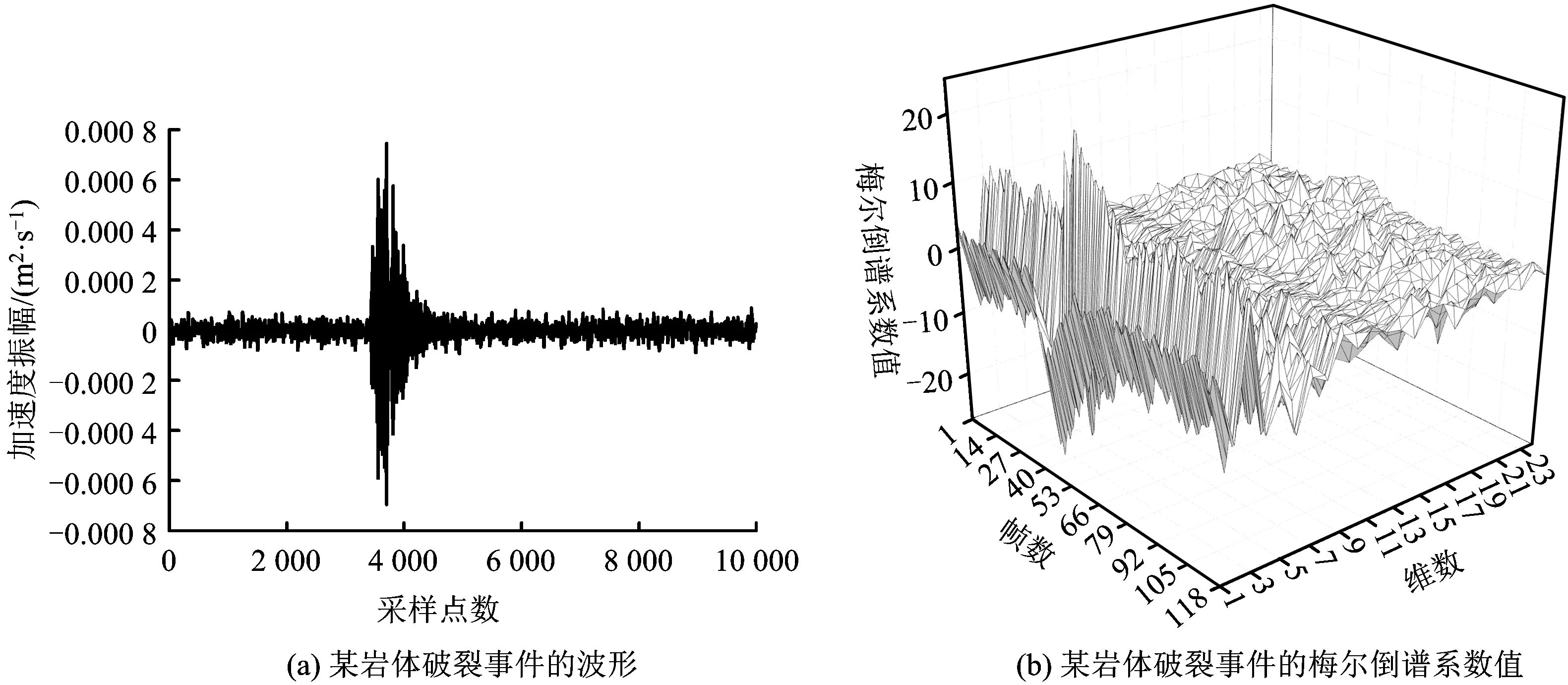
图3 某岩体破裂事件的波形及其梅尔倒谱系数值Fig.3 The waveform of a rock burst event and Mel-frequency cepstral coefficients

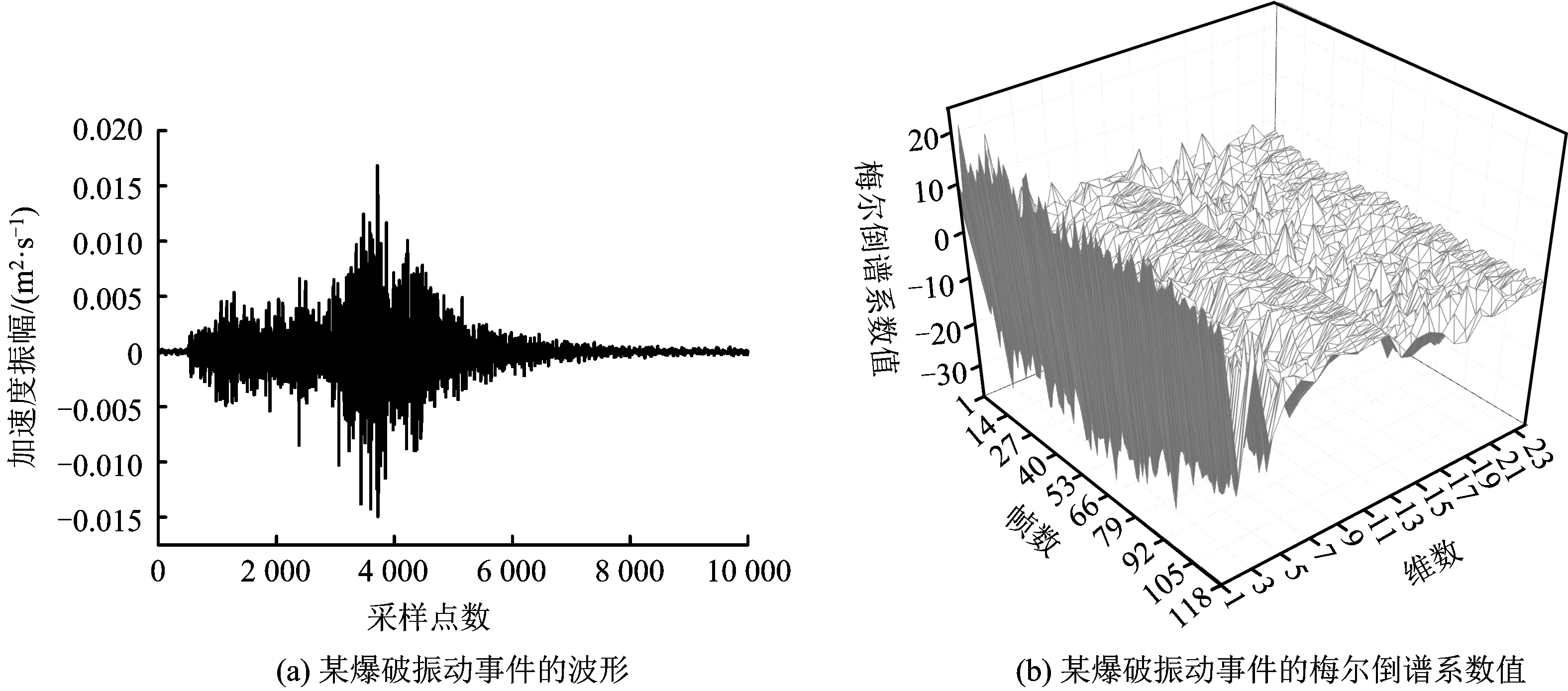
图4 某爆破振动事件的波形及其梅尔倒谱系数值Fig.4 The waveform of a blast vibration event and Mel-frequency cepstral coefficients

图5 某钻机凿岩事件的波形及其梅尔倒谱系数值Fig.5 The waveform of a rig drilling event and Mel-frequency cepstral coefficients

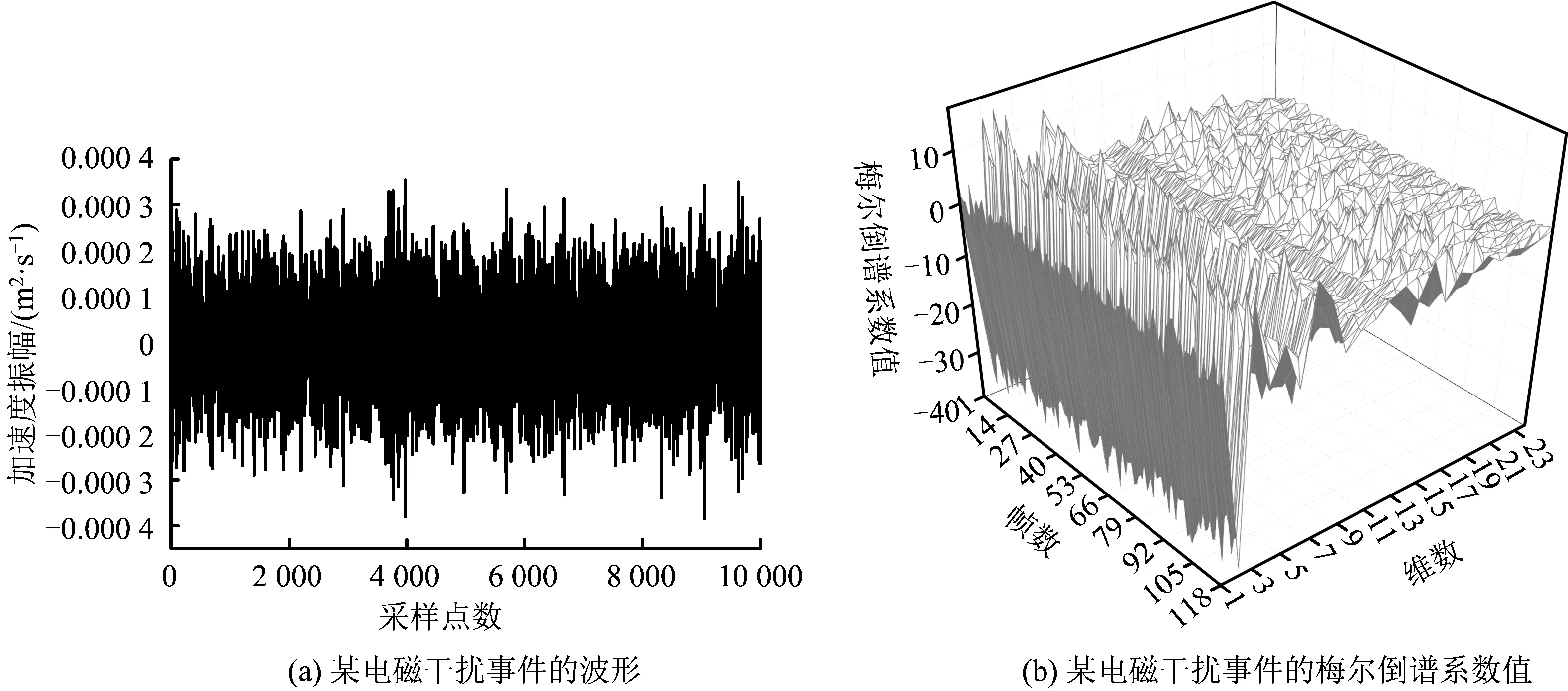
图6 某电磁干扰事件的波形及其梅尔倒谱系数值Fig.6 The waveformof a electromagnetic interference event and Mel-frequency cepstral coefficients

3.3 自动识别分类结果与分析

利用冬瓜山铜矿微震监测系统于2017年12月13日-2018年1月17日(其中2017年12月23日与2017年12月24日由于系统检修，监测系统没有数据)监测到的微震事件，对建立的混合高斯隐马尔科夫识别分类模型进行测试，所有事件均已经人工反复确认并进行类型标记，可作为计算模型识别准确率的依据。冬瓜山铜矿这一期间每日监测到的各类型微震事件的数量如图7所示。

根据图2的微震信号自动识别分类流程，对图7中所示的事件进行类型识别分类，并与人工标记的事件类型相对比，测试本文识别模型的准确率。

对于构建的自动识别分类模型，需要根据矿山实际情况确定相关模型参数：混合高斯方法中的高斯方程数目Q；马尔科夫链状态数N；马尔科夫链中观测值数M。其中，观测值M就是本文的梅尔倒谱系数的维数，即M=24。对于高斯方程数目Q，通过测试不同数目下的识别准确率进行选择。图8为识别模型中高斯方程数对识别准确率的影响分析，如图8所示，当Q≥3时，即可达到较高的识别准确率，但较多的高斯方程会加大模型的计算量，因此本文选用Q=4。同样，对于状态数N，通过测试不同的状态数N值进行对比。图9为识别模型中马尔科夫链状态数对识别准确率的影响分析，如图9所示，识别准确率随着N的增大而增大，但后续增加幅度较小，考虑到计算效率，本文实例中选用N=6。

根据上述选取的模型参数，对实际微震信号进行识别。每种事件识别的情况如图10所示。

由图7可知，2017年12月13日-2018年1月17日之间的微震事件总数为981个，其中：岩体破裂事件467件，爆破振动事件138件，钻机凿岩事件108件，电磁干扰事件268件。图10为识别模型识别后的每日各类型微震事件数量，由图10可知，岩体破裂事件识别错误数为26个，爆破振动事件识别错误数为32个，钻机凿岩事件识别错误数为2个，电磁干扰事件识别错误数为14个。因此，基于梅尔倒谱系数法的微震事件自动识别分类模型在该测试期间的识别准确率为92.46%，识别准确率较高。

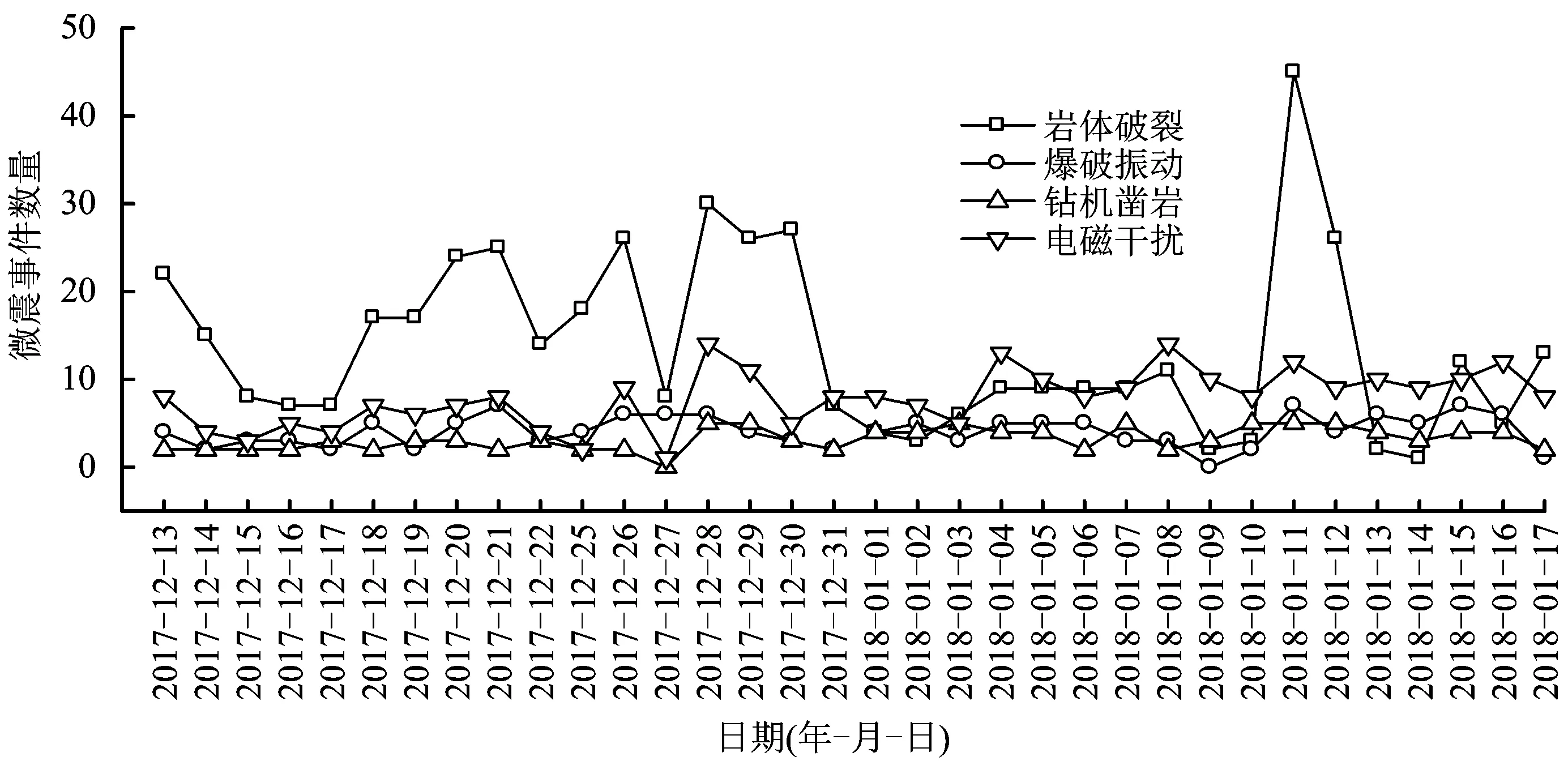
图7 冬瓜山铜矿2017年12月12-2018年1月17日每日微震事件数量Fig.7 Total daily microseismic events of Dongguashan copper mine from December 12, 2017 to January 17, 2018

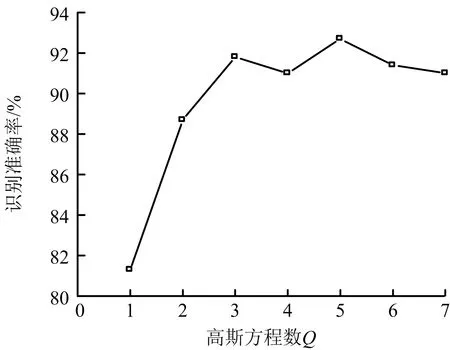
图8 识别模型中高斯方程数对识别准确率的影响分析Fig.8 Influence analysis of gaussian equation number on recognition accuracy in recognition model

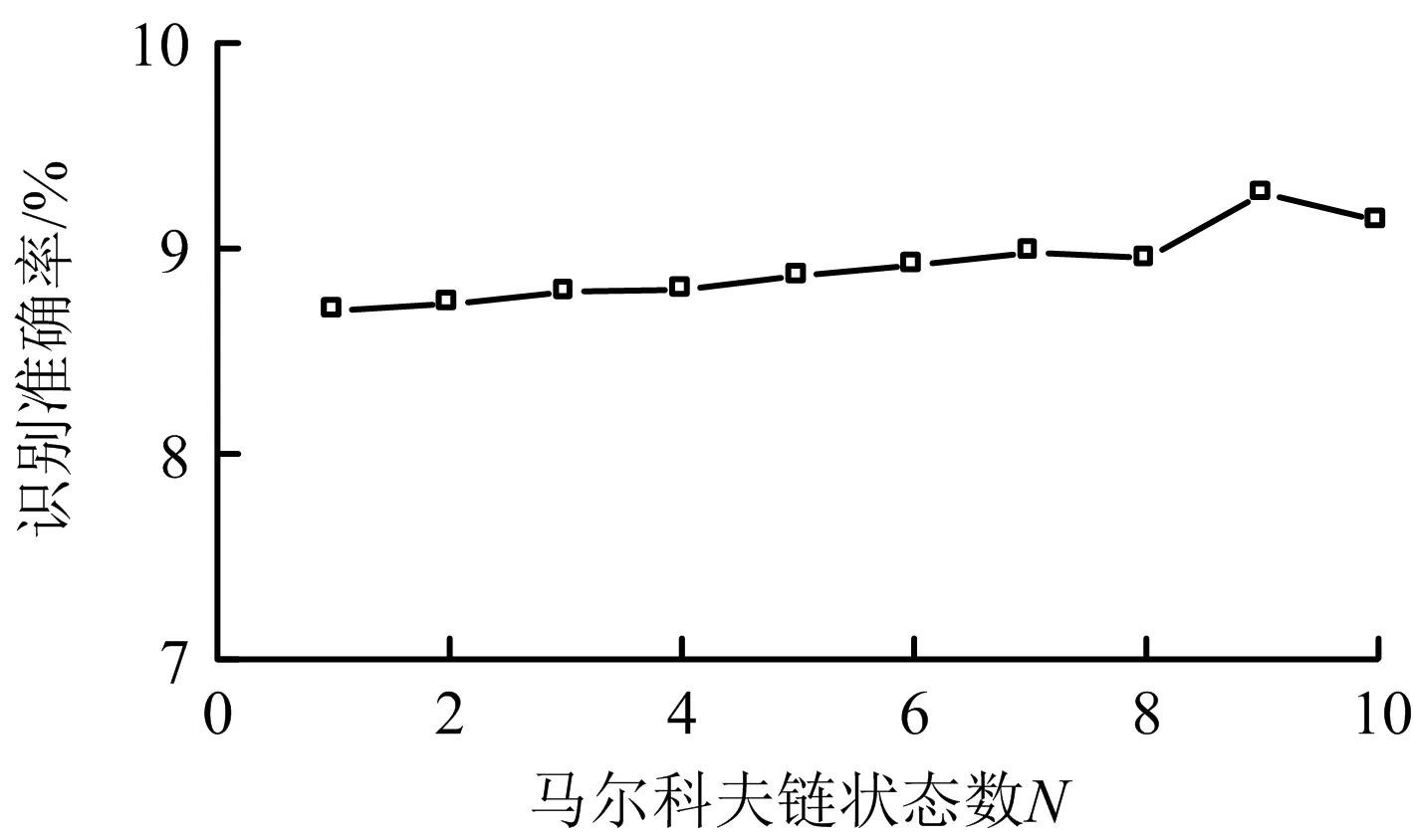
图9 识别模型中马尔科夫链状态数对识别准确率的影响分析Fig.9 Influence of the number of markov chain states on the recognition accuracy in the recognition model

从识别效果来看，基于梅尔倒谱系数与混合高斯隐马尔科夫识别模型的微震信号识别分类方法具有较高的准确率，可以用于常规微震监测系统的信号自动分类，以期提高微震信号分类的时效性和准确性，为矿山开采活动中的微震监测系统真正实现实时监测、实时分析提供了技术支撑。

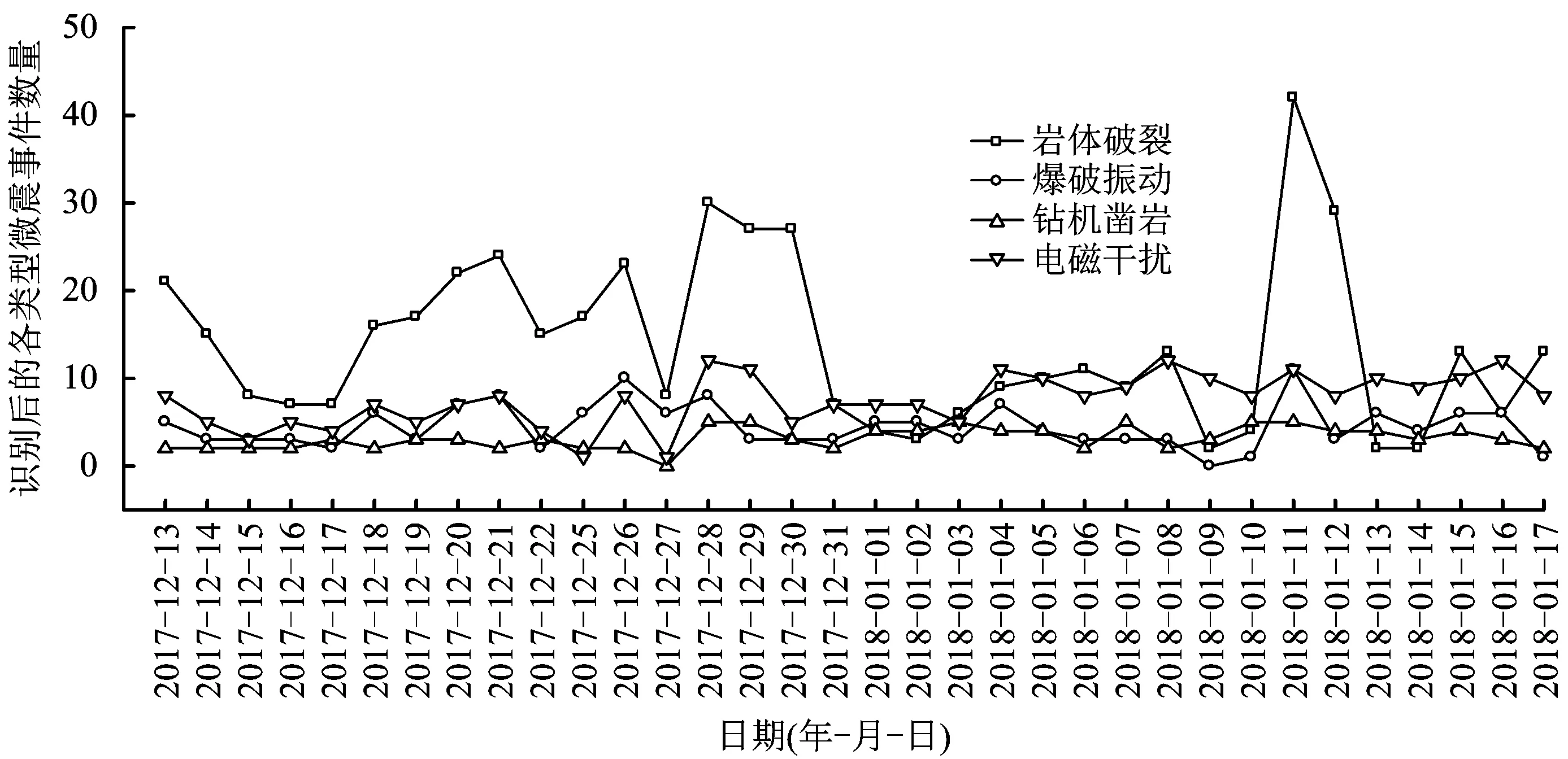
图10 识别模型识别后的每日各类型微震事件数量Fig.10 The number of each type of microseismic events per day after recognition of the model

4 结论

1)利用梅尔倒谱系数对波形进行特征提取，其原理是将频率域上的信号转化为梅尔频率域上的非线性频谱，并对其做离散余弦变换得到梅尔倒谱系数，结合梅尔倒谱系数差分运算，可以从波形中提取出24组特征向量，为信号的识别分类提供特征数据。

2)基于梅尔倒谱系数提取出的信号特征，训练构建4种微震事件对应的混合高斯隐马尔科夫识别模型，利用冬瓜山铜矿实际生产活动中监测的微震数据进行测试，识别准确率达到92.46%，具有较高的识别准确率。

3)基于梅尔倒谱系数的复杂微震信号自动识别分类方法适用于等长采样的微震监测数据和一定的数据基础。同时，该自动识别分类方法实现了矿山微震监测系统的高时效性，为实现微震监测系统的实时性分析提供了技术支持。