高压高速工况下弹炮间摩擦系数表征及数值模拟

李树立,杨国来

(南京理工大学 机械工程学院,江苏 南京 210094)

弹炮耦合过程中身管与弹丸构成的摩擦副的运行环境十分恶劣,通常伴随着高温、高速、高压、瞬时等极端工况,这会造成摩擦材料的表面发生氧化、相变、熔化等组织结构的变化,从而改变身管弹丸摩擦副的摩擦学状态,由此造成摩擦系数的改变。现阶段对于身管弹丸摩擦副的摩擦学状态的研究相对较少,在进行有限元仿真的过程中通常都是采用经验方法拟定单一摩擦系数进行有限元分析[1]。然而这与实际情况相差甚远,弹炮耦合过程中身管弹丸摩擦副伴随高温、高速、高压的极端工况,高温火药燃气以及摩擦副运动产生的摩擦热以及瞬态变形能大量积聚将会造成摩擦副摩擦状态的改变[2]。段海涛[3]通过研究低载高速干滑动下钢/铜摩擦副表面摩擦热,指出了速度和载荷对于摩擦热的影响规律,并在此基础上研究了摩擦热对于磨损机制的影响,获得了钢/铜摩擦副的摩损机制转变规律;谢挺[4]通过研究低载低速工况下摩擦磨损过程中金属材料表面损伤行为,对金属材料的磨损机制、失效形式进行了分析讨论。胡慧斌[5]采用MMS-1G型销-盘式摩擦磨损试验机对PCrNiMo钢/96黄铜摩擦副进行高温高速摩擦磨损试验,指出了摩擦副相对滑动速度和接触压力对身管弹丸摩擦副摩擦系数有不同的影响规律。

弹炮耦合过程中,弹丸在极短的时间内完成1 000 m/s左右的加速过程,单位时间内摩擦力大量做功,短时间热量难以耗散,从而积聚在摩擦副接触面附近[6],此外摩擦副接触面之间的接触压力通常能达到100 MPa左右,在如此高压的作用下,身管和弹丸的材料会发生剧烈的瞬态变形,两者接触处甚至产生一定的塑性变形,从而产生相应的塑性能,这对摩擦副接触面的热量累积起到促进作用,再加上高温火药燃气的作用使得摩擦副接触面温度接近甚至达到炮钢熔点,于是身管弹丸摩擦副将会逐渐形成液态金属流体膜,从而使摩擦副的工作状态由“碰撞”形式的干摩擦转变成动压润滑摩擦,而摩擦副接触面之间的这一层液态金属膜的存在起到了润滑剂的作用,导致摩擦副的摩擦系数显著下降。而摩擦副摩擦系数的改变对于弹炮耦合过程中身管弹丸的动态特性影响巨大,从而在很大程度上影响火炮的使用寿命。

综合身管弹丸摩擦副的干摩擦模型和熔融动压润滑模型,研究身管弹丸摩擦副摩擦系数与弹丸运动速度和身管弹丸摩擦副接触压力的关系,并在此基础上通过有限元方法模拟身管弹丸摩擦副摩擦系数改变,以此获取相应的内弹道性能参数,确定身管弹丸摩擦副摩擦学状态转变过程中身管和弹丸的动态特性变化,从而为弹炮一体化设计分析提供了一种技术途径。

1 身管弹丸摩擦副摩擦学状态的数学表征

弹炮耦合过程中身管弹丸摩擦副摩擦学状态主要包括干摩擦和动压润滑摩擦。

弹炮耦合过程中,身管弹丸摩擦副高温、高速、高压的极端工况导致短时间内身管弹丸摩擦副接触面附近热量大量积聚,致使接触面的材料产生氧化、相变、熔化等变化,与此同时造成摩擦副的摩擦学状态由最初的碰撞形式的干摩擦状态转变成了动压润滑状态。

火药燃气热、身管弹丸摩擦热、材料瞬态变形能等能量的累积,致使身管内膛表层发生热软化甚至热熔化,从而改变材料的物理参数,在身管弹丸摩擦副接触部分(弹带和膛线之间)形成一层动压效应的流体膜,将身管弹丸运动表面分割开来,这层金属液膜的存在,会对身管弹丸摩擦副的运动起到润滑作用,故称这层流体膜为动压润滑膜(动压润滑层)[7-12]。

在进行动压润滑层研究前做如下假设:

①金属软化层具有和金属流体层同样的流体特性;

②流体视为层流。

截取动压润滑层一部分进行受力分析,如图1所示。

x方向的流速为u;y方向垂直于接触面,流速可忽略不计。p为弹底压力,α为膛线缠角,τ为切向应力。

故控制体在x方向上受力平衡,如下式所示:

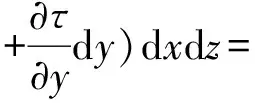
(1)

即

(2)

根据牛顿粘性定律,可知:

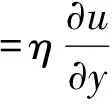
(3)

所以,

(4)

式中:η为熔融态弹带动力黏度。

将上式对y分别进行一次积分和二次积分,可得:

(5)

(6)

式中:A,B为常数。

考虑身管弹丸摩擦副动压润滑层属于层流,内膛表层(包括动压润滑层)速度与弹丸运动速度一致,动压润滑层的流速沿y向逐渐缩小,故而给定边界条件如下:

y=0,u=0y=h,u=v

由以上边界条件可以确定A和B的值,将计算后得到的值代入公式,可得动压润滑层控制体沿x方向的流速为

(7)

切向应力为

(8)

式中:h为动压润滑层的厚度。

由内弹道学可知,弹底压力为

(9)

故而,

(10)

式中:f0为火药力,ω为装药质量,ψ为形状函数,θ=0.2,φ为次要功系数,m为弹丸质量,v为弹丸运动速度,S为身管内膛截面面积。

故而,

(11)

式(11)第一项远小于第二项,故可以忽略第一项,由此:

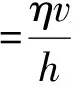
(12)

动压润滑层的厚度[7]h为

(13)

综合公式(12)、式(13)可得动压润滑层的摩擦系数为

(14)

式中:ρ1为弹带材料密度,η为熔融态弹带动力黏度,eL为弹带融化潜热,c为弹带比热容,tp为弹带熔点,t0为室温,k为动坐标下熔融层位置,l为弹带宽度,σ为接触压力。

动压润滑层的存在会导致身管弹丸摩擦副的摩擦系数显著减小,通过查阅相关资料以及综合相应的实验数据(如表1所示),得到身管弹丸摩擦副摩擦系数μ和σv的函数关系(σ为身管弹丸摩擦副接触压力),图2为μ-σv理论计算结果和实验测试结果。

表1 部分摩擦系数μ与σv数据

根据上文的动压润滑摩擦理论可知,弹丸初启动时,膛压以及速度较小,输入能量低,摩擦生热相对较小,火药燃气热、摩擦热的累积相对较小,摩擦副摩擦学状态表现为“碰撞”形式的干摩擦,相应的摩擦系数较大;随着膛压和速度的升高,摩擦副摩擦热大量积聚,再加上火药燃气和摩擦副瞬态变形能的累积,造成摩擦副接触面软化甚至熔化,形成动压润滑层,摩擦副摩擦学状态表现为动压润滑摩擦,由此造成摩擦系数显著下降。由图2可知理论计算结果和实验数据基本一致。

2 弹炮耦合动力学数值模拟

利用有限元数值模拟方法对某型舰炮弹丸膛内运动姿态进行数值分析时,针对整个物理过程做如下假设:

①假设火药气体压力在膛内分布为均匀分布,在任一身管横截面内压力值相等;

②不考虑身管的后坐运动,忽略弹丸前端空气阻力的影响。

2.1 有限元模型建立

根据某型号舰炮的实际结构尺寸建立有限元模型,身管内膛部分主要包括坡膛和膛线,弹丸部分主要包括弹体和弹带。弹带部分有限元建模过程中采用C3D8R六面体网格,并且弹带作为弹炮耦合过程中挤进运动的主要部位,进行了网格细化,以提高计算质量。表2给出了弹炮耦合过程各部件的网格单元数W和节点数J,图3为弹炮耦合过程身管弹丸摩擦副的网格图。

表2 弹炮耦合过程各部件网格单元数和节点数

2.2 摩擦子程序VFRIC建立

在身管弹丸摩擦副运动过程中摩擦剪应力不会无限制地增加,当摩擦剪应力达到一定程度之后,摩擦剪应力将不会增加。故而摩擦剪应力为

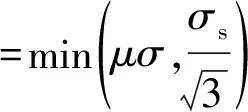
式中:μ为摩擦系数,σs为材料屈服应力。

图4为摩擦子程序VFRIC的流程框图。

2.3 有限元计算与分析

在有限元建模过程中,对于弹带和弹体采用Tie连接,以防止弹带和弹体发生相对运动;在不考虑后坐的情况下,弹丸膛内垂直和水平方向振动的来源主要是弹丸膛内受迫运动。弹丸膛内运动过程中弹丸与身管存在两处接触:一是弹带和膛线的接触,二是前定心与膛线的接触。为此建立此两处的接触对,接触算法采用罚函数法。此外由于忽略身管后坐运动,故而对身管后端面进行全固定约束。

本文通过加载弹底压力曲线作为弹丸运动的驱动力,以弹丸前端中心为研究对象,分别就身管弹丸摩擦副在恒定摩擦系数μ=0.1和变摩擦系数μ(σ,v)条件下,研究弹丸膛内运动的运动姿态。

弹丸前端振动位移与振动速度如图5～图8所示。图中,s2和s3分别为垂直方向和水平方向振动位移,v2和v3分别为垂直方向和水平方向振动速度。

由于重力作用以及组织装配等原因,弹丸初启动之后前定心部分与身管膛线会发生接触碰撞,由此造成每条膛线受力不均,从而致使弹丸产生振动。由图5和图6可以看出,不考虑身管弹丸摩擦副的转变过程,采用恒定摩擦系数μ=0.1进行弹丸膛内运动姿态研究时,弹丸径向振动(垂直和水平方向)位移较大,且起伏变化比较剧烈;而采用变摩擦系数μ(σ,v)模拟身管弹丸摩擦副摩擦系数转变,得到的弹丸垂直和水平方向振动位移相对较小且起伏变化较为平缓。

由图7和图8可以看出,不考虑身管弹丸摩擦副的转变过程,采用摩擦系数μ=0.1进行弹丸膛内运动姿态研究,弹丸径向振动(垂直和水平方向)速度较大,且起伏变化比较剧烈;而采用变摩擦系数μ(σ,v)模拟身管弹丸摩擦副摩擦系数转变,得到的弹丸垂直和水平方向振动速度相对较小,且起伏变化较为平缓,主要是由于弹炮耦合过程中存在的热软化及热熔化致使身管、弹带材料特性发生变化,影响身管弹丸摩擦副的摩擦学状态,从而致使身管弹丸摩擦副的摩擦学状态由碰撞形式的“干”摩擦转变为间接接触的动压润滑状态,在动压润滑状态下,首先由于摩擦系数的减小,弹丸运动相应的摩擦阻力也会下降,而克服摩擦力做功也会下降,更能够使每条膛线处的运动状态协调一致,从而在很大程度上减小由于每条膛线处受力不均而产生的振动[9-10]。

3 结束语

弹丸连发射击过程中,时刻面临着高温、高压、高速的极端工况,再加上连续发射时间过短,身管内膛不能冷却完全,致使连发射击过程中身管内膛温度呈累积上升趋势,由此造成身管内膛和弹带发生热软化和热熔化。本文运用动压润滑理论,建立身管弹丸摩擦副动态摩擦系数转变模型,此模型有效模拟了弹炮耦合过程中摩擦副状态改变带来的摩擦系数变化。其中,摩擦系数μ与接触压力和运动速度的乘积σv表现为负相关。当σv∈[0,2 000]时,摩擦系数较大;当σv∈[2 000,20 000]时,摩擦系数急速下降;当σv∈[20 000,50 000]时,摩擦系数趋于稳定,维持在0.02左右。此外,就变摩擦系数μ(σ,v)和恒定摩擦系数μ=0.1下对弹炮耦合过程进行研究,采用基于动压润滑理论的变摩擦系数μ(σ,v)计算的弹丸运动姿态相比恒定摩擦系数μ=0.1计算得到的弹丸运动姿态更为平缓。