无控火箭弹弹道失稳机理研究

樊会涛,杨林冲

(中国空空导弹研究院,河南 洛阳471009)

在空空导弹研制中,无控火箭弹是一种过渡状态,用于评估火箭发动机在飞行条件下的稳定性、安全性,并初步了解导弹的气动特性、弹架分离安全等情况。出于载机安全考虑,在有控弹空中发射试验之前通常安排若干数量的火箭弹进行地面/空中发射,历史上曾经出现过火箭弹弹道明显摆动的现象。

为适应现代战争对速度、射程、机动性及内埋挂装等要求,先进空空导弹相对于上一代产品,弹身更修长,表面更整洁,气动面更窄小[1]。先进空空导弹火箭弹弹道不平稳的现象非常明显,地面发射稍好,空中发射情况尤其恶劣,去掉导弹前翼面后,反而出现了更坏的情况。

按照传统的飞行力学理解,无控火箭弹在一定条件下出现摆动是弹体动力学中的固有现象,但由于无控火箭弹本身是静稳定的,因此弹体的摆动也不会持续地增大[2-3],更不应当发散。然而在先进空空导弹研制中却出现了弹道发散的现象,甚至直接引起导弹解体的飞行故障。以前工程实践中抑制火箭弹摆动的技术措施也失去了作用。

文献中对于火箭弹的弹道稳定性问题有很多不同程度的分析研究,但研究对象主要集中在兵器领域的无控火箭弹,其本身作为最终交付产品并且地面发射。对于空空导弹的无控火箭弹,它首先不是最终交付产品,仅仅是产品研制中的一种过渡状态;其次,空空导弹作为打击空中机动目标的精确制导武器,它的气动外形、发射方式与兵器领域的无控火箭弹有着本质的差别。因此,有必要对先进空空导弹火箭弹出现弹道失稳现象、导致飞行故障的物理机理,需要采取的技术措施开展深入研究。

1 无控火箭弹动力学模型

为研究火箭弹弹道失稳的机理,建立如下无控火箭弹动力学模型[4]。

1.1 火箭弹弹体纵向运动的线性化模型

按照经典的飞行力学理论,弹体纵向姿态运动方程可简化为

(1)

式中:ϑ为弹体俯仰角,θ为弹道倾角,α为攻角,δ为纵向通道舵偏角,a1为阻尼系数,a2为静稳定系数,a3为舵效率系数,a4为法向力系数,a5为舵升力系数。

据此,纵向运动(俯仰/偏航)舵偏角到攻角之间的传递函数为

(2)

由于a1a4+a2≫a5,因此τ≈0。式(2)可简化为

(3)

1.2 弹体的横向(滚转)运动的线性化模型

弹体的滚转运动方程可简化为

(4)

式中:c1为横滚阻尼系数,c3为横滚舵效率系数,γ为导弹横滚角。

横滚舵偏角δx到滚转角速度ωx之间的传递函数为

(5)

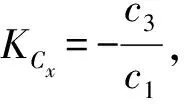
1.3 纵向运动与横向运动之间交叉耦合的导弹空间运动方程系

为了更好地分析火箭弹摆动的原因,列出考虑了纵向运动与横向运动之间交叉耦合的导弹空间运动方程系为

(6)

式中:a1～a5为前文已述及的弹体纵向运动动力学系数;ωz,ωy和ωx分别为弹体俯仰、偏航和横滚角速度,ωz和ωy是前文ωn具体的两项;αI,αII和δI,δII分别为2个纵向通道(俯仰/偏航)的通道攻角和通道舵偏角,δIII为横滚通道舵偏角(同前文中的δx)。ΔMIII(δIII)为横滚通道驱动力矩项,它反映的是三通道舵偏(通常是安装误差)引起的横滚力矩;Mxk0(αI,αII,δI,δII)为斜吹力矩项,它反映的是纵向运动对横向运动的影响。ωxωy和ωxωz为陀螺效应项,ωxαII和ωxαI为惯性项,它们代表的是横向运动对纵向运动的影响。

2 火箭弹弹道失稳机理分析

本节利用前面建立的火箭弹动力学模型对火箭弹弹道失稳机理进行数字仿真研究。

2.1 无控火箭弹飞行弹道上的压心、质心变化特性

导弹的相对静稳定度用质心与压心之间的距离占全弹长度的百分数(η)来表示。空空导弹的燃料布置于后弹体,主动段质心持续前移,一般理解其静稳定度在主动段应持续增加。但实际上还必须考虑全弹气动压心的变化:主动段导弹速度剧烈增加,压心快速前移,从这个角度来讲静稳定度又是在减小的。导弹静稳定度受质心、压心二者变化的综合影响,是它们“赛跑”的结果。这样在分析火箭弹的静稳定度时,就不能仅仅分析初始状态的质心、压心相对位置,而要进行全弹道的动态分析。图1是某火箭弹飞行弹道上的相对静稳定度变化曲线,注意到在主动段(前13 s)其相对静稳定度是先增加后降低再增加的。

2.2 火箭弹弹道共振现象的必要条件

通过质点弹道数字仿真,可得空中发射火箭弹在整个飞行过程中纵向运动频率ωy(t)的变化曲线和横向运动(横滚)频率ωx(t)曲线,如图2所示。ωy(t)在发射条件(高度、速度和仰角)确定后就被唯一确定了;ωx(t)的高低则是不固定的,它不但受发射条件的影响,还要由具体的等效安装误差(将所有的横向不对称因素都等效进去)来决定,ΔδIII增加,ωx的曲线抬高,反之下降。

在图2中弹体纵向运动频率与横向运动频率(滚动转速)有两处相等,在这两个点上具备了传统意义上的弹道共振的必要条件。具体到每一枚火箭弹,由于ΔδIII的不确定性,弹道上会不会出现频率相等的点(或相近的区域)、何时出现都具有很大的不确定性。并且在频率相等的点上(或相近区域)弹道仅仅是短时间的共振还是维持长时间持续共振同样也是不确定的。短时间的弹道共振一般不会引起导弹过载的持续增加且会自行消失,危害不大,而长时间共振就可能引起弹体过载的持续增加,甚至引起故障。

弹道明显摆动(共振)的发生需要同时具备2个必要条件:纵横向运动频率相近、纵向通道存在一个不可“忽略”的等效舵偏δI/δII(舵面安装误差、弹体的轴线不对称、弹体的弹性变形和发动机推力偏心等因素都可引起),由它激励出一定量值大小的攻角,引起弹道摆动。纵横向频率相近的前提是客观上存在一个不可“忽略”的等效ΔδIII,它“驱动”火箭弹的自转转速达到纵向运动频率附近。

2.3 火箭弹弹道持续共振现象的内在机理——似月运动和转速闭锁

从前面的数字仿真结果注意到,空空火箭弹在全弹道上纵向运动与横向运动频率相同的点只有2个并且很快便错开了,但实际的飞行试验中却出现持续的共振摆动,有必要对此进行分析。

空空导弹采用轴对称气动外形,相对滚转角Φ的定义见图3,在攻角存在的情况下,它直接决定气流吹到导弹的方位。导弹的诱导滚转力矩Mxs与攻角α的大小正相关。攻角一定时,诱导滚转力矩Mxs是相对滚转Φ的正弦函数,四分之一圆周上Mxs与Φ关系曲线见图4所示,圆周的其余部分呈周期变化。

考虑了诱导滚转力矩Mxs后,火箭弹的滚转方程(4)可写为[2-5]

(7)

式中:kxw为导转力矩系数,kxz为滚转阻尼力矩系数,kxs为诱导力矩系数。

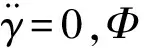
如果似月运动长时间的持续下去而不被打破,火箭弹转速将一直被锁定在共振转速附近,称为“转速闭锁”。“转速闭锁”会导致攻角急剧增大,形成长时间阻力增大和弹道发散,出现“灾变性偏航”,导致近弹和掉弹[5]。过大的攻角甚至使得导弹横向力超过设计极限而造成火箭弹空中解体。

2.4 对火箭弹飞行故障的数字仿真研究

针对先进空空导弹火箭弹空中发射试验飞行故障,利用前文动力学模型开展数字仿真研究。该次试验情况如下:火箭弹不带前弹翼,载机平飞,发射海拔高度8 600 m,飞行马赫数为0.9。发动机点火后,机弹分离正常。初始段弹体有小幅摆动,并很快减弱。4.5 s时前弹道平直,发动机尾焰稳定。4.7 s时弹体明显开始旋转摆动,起初幅度较小,5.6 s时幅度增大,接着摆动加剧,到7.7 s时发动机解体。共进行8次摆动,频率约2.0～2.6 Hz,呈逐渐增大趋势,最大摆动幅度达28°,如图6所示。7.3 s时发动机尾部出现明显的高亮度火团,持续0.4 s到7.7 s发动机出现一团火光,空中解体,火箭弹前弹体向前继续飞行一段后掉落。

由于在发射前没有进行测量,只能假设一组工程上可能的气动面安装误差(δI=Δ1,δII=Δ2,δIII=Δ3)、发动机推力偏心数值(ε=Δ4)进行数字仿真来复现故障[6]。图7为该次空中发射火箭弹纵向运动频率和横向运动频率曲线。注意到,从4.4 s开始一直到7.7 s火箭弹的纵向运动频率和横向运动频率一直非常接近,为弹道共振创造了必要的条件。图8为地理坐标系下观察到的攻角曲线,由于导弹是滚转的,它呈现出交变的特征。图9是弹体系下火箭弹的过载变化曲线,火箭弹的过载持续增大而超过设计范围,加之在弹体周向上方位保持不变,最终导致发动机在这个非工况过载环境下工作而烧穿壳体,引起空中解体的飞行故障[7]。

2.5 无控火箭弹飞行弹道稳定性影响因素

本节按照前文故障复现所采用的数学模型和发射条件进行数字仿真研究,探讨不同的初始输入条件对无控火箭弹飞行弹道稳定性的影响情况。

①输入条件1。

舵偏角安装误差:δI=Δ1,δII=Δ2,δIII=Δ3;

发动机推力偏心:ε=Δ4;

该组输入条件是2.4节中故障复现所采用的,计算结果作为对比研究的基准。

②输入条件2。

舵偏角安装误差:δI=0.5Δ1,δII=0.5Δ2,δIII=Δ3;

发动机推力偏心:ε=Δ4;

该组输入条件相对于条件1,纵向通道等效舵偏误差角降低一倍。仿真结果显示火箭弹的纵向运动频率和横向运动频率曲线与图7相同,攻角曲线和过载曲线相对于图8、图9相应地降低了一倍左右。

③输入条件3。

舵偏角安装误差:δI=Δ1,δII=Δ2,δIII=0.5Δ3;

发动机推力偏心:ε=Δ4;

该组输入条件相对于条件1,横向通道等效舵偏误差角降低一倍。计算结果见图10和图11。注意到,图10中的纵向运动频率、横向运动频率相差较大,保持在7 rad/s以上,不具备弹道共振的必要条件,图11的攻角很小。

④输入条件4。

舵偏角安装误差:δI=Δ1,δII=Δ2,δIII=Δ3;

发动机推力偏心:ε=Δ4;

该组输入条件与条件1相同,是故障复现采用的条件。但火箭弹的质心通过配置前移后,保证整个飞行弹道导弹的静稳定度在10%以上。仿真结果显示,火箭弹的纵向运动频率和横向运动频率相差较大,保持在6.5 rad/s以上,类似于图10已经不具备弹道共振的必要条件,激发的攻角很小。

先进空空导弹为适应现代战争对速度、射程和内埋挂装的新要求,横向尺寸、气动面面积被大幅度压缩,唯有大幅降低导弹的静稳定度才能满足机动性(操纵性)要求。去掉前翼后,导弹横向阻尼系数被明显降低,在其他条件不变的情况下,导弹的横滚频率上升得更快,更容易到达纵向频率附近,发生持续弹道共振的可能性大幅提高。相对于地面发射,火箭弹空中发射时整个主动段的飞行速度更高,压心前移的现象更加突出,火箭弹横滚频率上升得更快,更容易到达纵向频率附近。这就解释了为何先进空空导弹更容易出现弹道失稳,空中发射情况更糟糕,去掉前翼的传统措施为何“事与愿违”。

3 保证无控火箭弹飞行稳定的措施

通过前面的数字仿真研究并结合工程实践,为避免火箭弹飞行弹道的不稳定现象,提出如下的技术措施:被动措施和主动措施。被动措施就是除了保证弹体各舱段的连接精度,舵面、翼面和电缆整流罩等的安装精度、对称度以外,对每一片舵面、翼面的零位偏差要控制在0.2°之内,所有舵面零位偏差的代数和小于0.3°,翼面的也要小于0.3°,且避免上述2个代数和同号;保证舵面、翼面的刚度和强度满足要求;按指标要求严格控制发动机的推力偏心。主动措施就是严格控制火箭弹的质心位置,必要时通过配重将其向前调整,将全弹道的静稳定度控制在10%以上。无控火箭弹作为空空导弹工程研制中的过渡状态不需交付用户,对气动面的选配安装、质心位置的适度调整是可行且有意义的。

被动措施、主动措施的本质都是降低或避免纵横向通道之间的相互耦合。前者通过大幅减小导弹的横滚频率使得ωx远小于纵向固有频率ωy,相当于尽力压低图2中ωx(t)曲线的高度,使其在整个弹道上都处在ωy(t)的下面,且保证一定安全距离。后者通过增加纵向固有频率ωy,相当于尽力抬高图3中的ωy(t)曲线的高度。另一方面被动措施通过降低等效的纵向通道舵偏面偏差,来降低激励输入(即干扰攻角)。主动措施通过提高导弹静稳定度,使得单位舵偏引起的干扰攻角明显减小,直接抑制了弹道的摆动幅度,相对于被动措施效果更直接、更明显。

必须克服火箭弹结构简单、技术含量不高的麻痹思想。由于缺少飞行控制系统,没有引入人工增稳装置,火箭弹的弹道稳定性全靠自身的静稳定度储备来保证。为避免人为地引入干扰,对外形的几何对称性要求更高,对火箭弹的加工、安装精度的控制必须从严。先进空空导弹火箭弹综合采用被动措施、主动措施后的数字仿真结果显示火箭弹飞行弹道平稳,且已通过飞行试验验证。

4 结束语

本文揭示了空空导弹火箭弹弹道失稳的机理,对型号研制中出现的弹道失稳问题进行了研究。先进空空导弹采用放宽静稳定度外形设计,使得无控火箭弹纵横向运动耦合共振变得更加容易、频繁,共振的强度更加剧烈。

避免火箭弹纵横向运动耦合共振发生的技术措施分为被动措施和主动措施,被动措施通过限制以舵翼面安装误差为代表的各类工程误差,来抑制火箭弹滚转的角速度、干扰激励输入,消除弹道共振现象发生的外因。主动措施通过前移火箭弹的质心来增加其静稳定度,进而提高其纵向运动的抗干扰能力,同时也增加了火箭弹的纵向运动固有频率,消除弹道共振现象发生的内因。

纵横向运动耦合共振问题是无控火箭弹所特有的。最终交付用户的空空导弹都是带有控制系统的,其横滚角被控制在零值附近很小的一个范围内,并且正反2个方向来回波动,不会出现上述问题[8]。