基于多普勒信息的炮位侦校雷达外推算法研究

谢 恺,秦鹏程

(陆军炮兵防空兵学院,安徽 合肥 230031)

炮位侦校雷达是保障炮兵全天候、全天时获取战场情报信息不可或缺的重要侦察装备[1]。数据处理方法是决定炮位侦校雷达性能的关键技术之一[2]。随着新型炮位侦校雷达技术的发展,可以精确测量弹丸多普勒信息。由于多普勒信息中包含了弹丸的位置、速度等信息,充分利用多普勒信息可完善传统弹丸测量模型。由于技术原因,传统的炮位侦校雷达数据处理中,通常没有应用多普勒信息[2-3]。针对上述问题,王庭辉等提出了一种基于最小二乘拟合并充分利用径向速度数据的新的目标运动参数估计策略[4];WU等也是将径向速度纳入弹道方程,建立了一种新的弹道运动模型[5]。但上述算法没有针对炮位侦校雷达对多普勒信息进行详细建模,且未用真实的炮位侦校雷达数据对算法进行分析验证。

为了进一步提高外推算法的优化性能,本文对炮位侦校雷达高精度的多普勒信息进行建模处理,并将速度信息作为第四维观测向量纳入测量方程,完善弹道模型,以提高弹道目标参数估计的精度,构建基于多普勒信息的七维状态向量弹道外推模型[6]。并在此基础上进行无迹卡尔曼滤波处理,以充分利用测量信息,提高算法的定位精度。最终提出了基于多普勒信息的七维状态向量无迹卡尔曼滤波算法(七态DB-UKF算法),并结合真实弹道数据进行了仿真实验。

1 弹道模型

1.1 状态方程

通常情况下,弹丸运动系统状态空间表达式要结合弹丸运动模型来选取,对于射程不大的火炮,通常使用质点弹道模型,取弹丸位置和速度变量作为状态变量[7]。现有的卡尔曼滤波方法中弹道系数是在每次滤波过程中以其为常数的条件下,将相邻两点的速度、加速度滤波值代入弹道方程进行粗略估计求得的,这种估计形式存在较大的误差,甚至超出了弹道系数的理论范围,只能采用硬限幅的方式对其进行限制。

本文采用非线性估计的方式求解弹道系数,将其纳入弹道方程,进行滤波处理和参数估计[6]。为此,定义状态向量为

x=(x1x2x3x4x5x6x7)=(xyzvxvyvzCb)

(1)

式中:(x,y,z)为弹道的位置(坐标)诸元;vx,vy,vz为弹道的速度诸元;Cb为弹道系数。

弹丸质心运动微分方程可当作状态方程写为

(2)

1.2 观测方程

通常情况观测量是状态变量的线性组合,一般为雷达到弹丸的距离Rr、方位角α、俯仰角β,加入速度信息v后,可表示为

y=(Rrαβv)

(3)

雷达系统的测量方程可写成如下的形式[4-5]:

(4)

式中:U为零均值高斯白噪声,其方差为Q。为得到测量向量中的速度信息,对多普勒信息作出以下处理。

任意t时刻运动目标的多普勒频率fd(t)(隐含t)为[8-9]

(5)

式中:λ=c/fc为雷达的工作波长信号,传播速度取为光速c。因此,弹丸的径向速度可表示为

(6)

多普勒频率fd可通过雷达多普勒滤波器组数据加权得到。

某新型炮位侦校雷达的俯仰项测量采用频扫体制,频率fc与天线俯仰角θ存在映射关系[10],可表示[9]为

(7)

式中:θ为波束指向方向,λ0为基准波长,f0为基准频率,l为连接相邻频向单元的线长度,d为线阵间隔距离,l/d为重叠因子。频率、方向的对应关系在实际雷达装备的工程实践中常以表格形式体现,如表1所示。

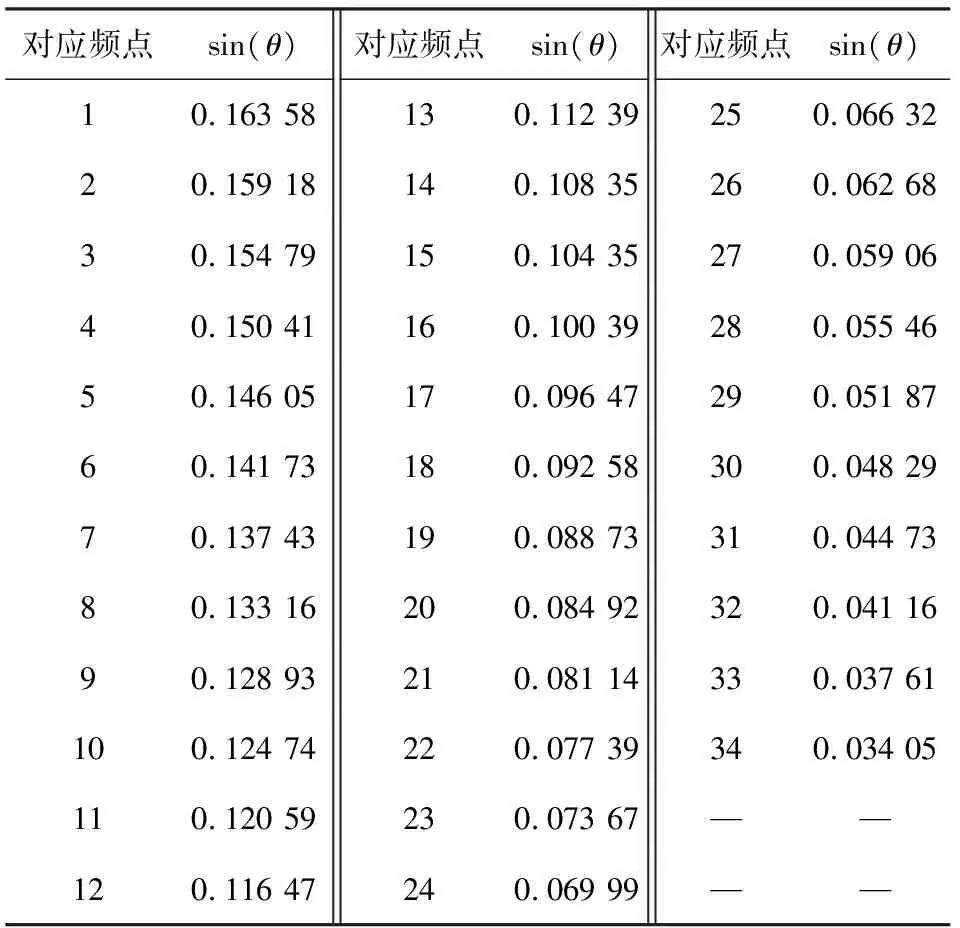
表1 频扫天线频率、方向对照表

表1中显示了34个频点对应的指向角正弦值。频扫天线电磁信号的频率fc对应各波束指向θ,表中最低频率点为9 GHz,步进频率为20 MHz。

随着新型炮位侦校雷达技术的发展,测角精度得到有效提高,按表1对应得到的信号频率准确度也相应提升;此外,随着雷达信号处理硬件资源更丰富,多滤波器组组数增加,得到的多普勒频率测量精度更高。因此,由式(6)得到的多普勒速度信息具有较高的精度。为验证多普勒速度信息的精度,对式(6)求导:

(8)

将某新型炮位侦校雷达的典型参数代入式(8),可得多普勒速度误差约为0.5 m/s。

2 无迹卡尔曼滤波(UKF)方法

UKF通过使用确定性采样点来近似非线性分布的矩,它以UT变换为基础,采用线性最小均方估计的更新框架来进行时间递推。UKF的计算量与扩展卡尔曼滤波(EKF)处于同一量级,但不需要求导计算Jacobian矩阵,可以处理不可导的非线性函数,而且非线性分布统计量的计算精度至少达到2阶,性能优于EKF[11-12]。以下为UKF算法。

将式(2)、式(4)离散化,可得非线性高斯离散时间系统:

(9)

式中:x(k)∈Rnx为系统在k时刻的状态,y(k)∈Rny为k时刻的观测量;V(k)和U(k)分别为加性过程噪声和测量噪声,其协方差分别为R和Q。考虑一个L维高斯随机变量x,经过非线性变换后得到:

y=g(x)

(10)

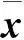
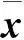
(11)

(12)

(13)

通过下列方法可以计算变量y的均值和方差:

Yi=g(Xi),i=0,1,…,2L

(14)

(15)

(16)

针对式(9)～式(16)描述的系统,UKF算法流程如下。

①初始化。

(17)

②计算样点。

(18)

③时间更新。

Xk|k-1=f[Xk-1]

(19)

(20)

(21)

Yk|k-1=h[Xk|k-1]

(22)

(23)

④测量更新。

(24)

(25)

(26)

(27)

(28)

3 仿真及分析

本文以122榴弹为例,利用靶场弹道精密测量雷达数据,进行数值仿真计算,主要仿真条件如下。①弹丸发射条件:初速v0=700 m/s,射角θ0=19.5°;②取雷达测量误差:σr=6.5 m,σβ=σε=1.5 mil,σvr,d=0.4 m/s;③雷达距离炮位15 km,雷达初始采样点的俯仰角为3.1°,采样间隔300 ms,从初始采样点继续探测18个弹道点后采样中止。采用两点差分法对状态进行初始化。

分别建立六维状态向量三维观测向量、七维状态向量三维观测向量的弹道模型,用EKF、UKF对雷达测量数据进行处理[14],同时,在以上算法观测信息中加入多普勒速度形成基于多普勒速度信息的滤波算法,并重复上述过程,得到外推起点,用龙格-库塔法[15]外推发射点。进行10 000次蒙特卡洛仿真实验,得到每种算法的定位精度圆中间误差(Ecp)[16]、算法所需时间、弹道系数误差、位置误差以及速度误差。

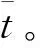
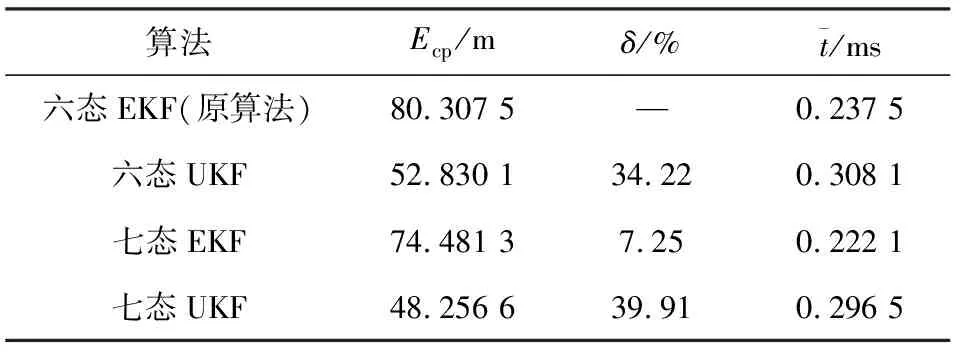
表2 外推算法仿真对照表

接下来对应用多普勒信息的各算法进行分析,比较其优化效果。

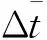
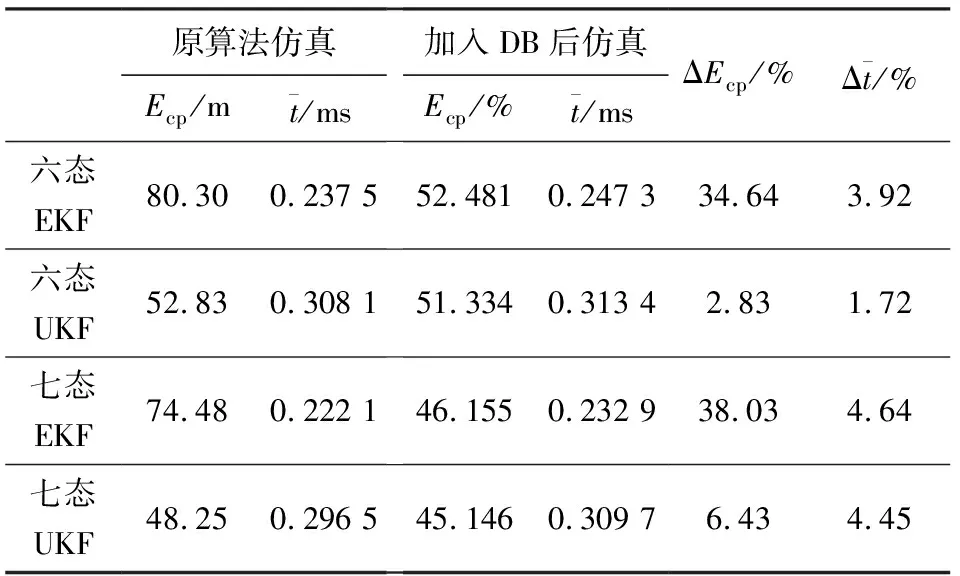
表3 多普勒信息优化效果对照表

由表3可以看出:上述各算法的计算量处于同一量级,应用多普勒信息后,使用EKF的外推算法定位精度优化幅度比使用UKF外推算法的优化幅度要高;使用七态滤波外推算法定位精度优化幅度比使用六态滤波外推算法的优化幅度要高。为分析以上算法改进项取得的优化效果,对考虑多普勒信息前后,各算法位置、速度、弹道系数误差进行了比较,图1～图3所示。

图1给出了10 000次蒙特卡洛仿真中,滤波得到19个雷达采样点(N)位置均值与精密测量雷达数据相应各点差的均方根值Rp。由图1可以看出:将多普勒信息纳入观测方程后,六态EKF外推算法的位置误差略有上升;六态UKF外推算法的位置误差有较大幅度的下降;七态EKF、七态UKF外推算法的位置误差有少量增加。

图2给出了10 000次蒙特卡洛仿真中,滤波得到19个雷达采样点速度均值与精密测量雷达数据相应各点的差的均方根值Rv。由图2可以看出:应用多普勒信息的六态算法和七态EKF外推算法可以有效降低滤波终点的速度误差,而应用多普勒信息的七态UKF外推算法滤波终点的速度误差与原来处在同一水平。

将靶场弹道精密测量雷达数据相邻两点的速度、加速度滤波值代入弹道方程,求得弹道系数[4],作为仿真中的真实弹道系数。六态算法利用仿真雷达数据,按上述方式求得弹道系数;七态算法通过滤波得到弹道系数,弹道系数性能对比如图3所示,图中S为仿真次数。是否加入多普勒信息对六态算法中弹道系数精度基本没有影响,如图3(a)、图3(b)所示。而由图3(c)、图3(d)可以看出:考虑多普勒信息的七态滤波外推算法的弹道系数误差RC有较大幅度降低,且误差值均低于0.05。

综上所述,可以得到以下结论:①EKF滤波估计精度相对较低,加入高精度的多普勒信息后能大幅度降低估计误差,提高定位精度,结果如表3中六态EKF、七态EKF外推算法结果所示。②七态滤波外推算法将弹道系数纳入状态方程。因此,弹道方程中考虑多普勒信息,能有效提高弹道系数的估计精度,进而降低外推误差。但加入多普勒信息对六态算法的弹道系数精度没有太大影响,而UKF算法本身又具有较高的估计精度,因此,加入多普勒信息后参数估计优化效果较小,会出现表3中六态UKF定位精度提高幅度不大的现象。③由于位置误差造成的影响将会直接叠加在外推落点上,而外推过程中的弹道系数误差、速度误差却通过误差累积使其影响不断扩大。虽然在图1中六态EKF、七态外推算法应用多普勒信息后算法的位置误差稍有增加,但位置误差主要是平移到定位误差上,与速度误差、弹道系数误差等放大到定位误差的累积效应相比,基本可以忽略。因此,外推得到的炮位仍然具有较高的定位精度。

4 结论

本文针对传统炮位侦校雷达观测信息中对多普勒信息利用不完整的情况,提出针对具体炮位侦校雷达的多普勒速度信息作为第四观测维,综合各算法改进项建立基于多普勒信息的七态UKF外推算法。对新算法位置误差、速度误差、弹道系数误差进行分析,总结取得外推精度、效率优化效果的影响因素。该算法提高了弹道系数等参数估计精度,仿真分析与实验结果表明:在同一计算水平下,该方法具有更高的定位精度。

本文基于单个系统模型进行了弹道外推,如果遇到目标运动状态与模型不符时,会引起较大误差。下一步将对交互多模(IMM)算法进行研究,使用2个或更多的模型来描述弹道外推过程中的系统状态,最后通过有效的加权融合进行系统状态估计,增强了模型的适应性。