沪深300股指期货对现货波动性的影响

吴署生，吴其文，李维颖

（1.长江大学 城市建设学院，武汉 434023；2.中国科学技术大学 管理学院，合肥 230026）

关键字：协整检验；GARCH模型；股指期货

引言

2010年4月16日，我国资本市场推出沪深300指数期货合约，分散了股票市场的系统性风险，进一步完善了我国的资本市场。然而，股指期货推出后，沪深300指数大跌，下跌890多点，跌幅达到26.56%，让人们不禁怀疑股指期货对市场稳定的作用。2015年6月份股票市场又是一轮暴跌，沪深300指数下跌2328点，跌幅高达43.48%。新一轮大跌使得众多投资者都认为股指期货恶意做空导致市场持续下行，连监管部门都作出了限制做空和提高保证金的举措，使得投资者进一步怀疑在中国还不成熟的资本市场，股指期货的推出是否正当其时。因此，无论从投资者还是监管部门的角度，都需要对股指期货作进一步研究。

一、文献综述

国外早在20世纪90年代就对股指期货进行了深入研究。Hodgson和Nicholls（1991）分析了引进股指期货后澳洲所有普通股的波动情况，发现股指期货并没有加大澳洲股市的波动。Antonious et.al（1995）研究了DAX指数1987—1993年的情况，认为股指期货降低了现货市场的波动性。Sung and Kwon等（2004）对韩国股票和现货市场的研究表明，股指期货的推出会使得整个市场的波动和效率提高，股指期货成分股的波动要小于非成分股的波动。

随着股指期货的推出，国内的研究也不断深入。李雪明（2014）通过误差修正模型对股指期货679个交易日的实证研究，得出沪深300股指期货价格的对数序列与沪深300指数的对数序列之间存在长期稳定的均衡关系，二者之间的联动效应长期有效。王志敏（2015）通过协整检验和GARCH模型对IF1403研究，得出股指期货上市交易降低了其指数的波动性，但降低程度不是很大，其对市场冲击的反应比西方发达国家更剧烈。

二、协整检验和波动性分析

（一）模型介绍

由于金融时间序列通常是不稳定的，我们通常可以通过差分来让数据平稳，再进一步分析序列的波动性和序列间的因果关系等，还可以通过协整关系来刻画两个序列之间的关系。

1.协整检验

本文采用EG两步法来进行协整检验。第一步，检验两组序列平稳性，如果是同阶单整，对序列进行回归：

第二步，对回归得到的残差进行ADF检验，如果在5%的显著性下通过检验，则说明序列之间存在协整关系，即序列有着同涨同跌的特点。

2.ARCH和GARCH模型

由于金融数据的波动聚集现象导致模型残差不满足同方差。ARCH模型在均值方程的基础上，引入了波动性方程，将每一个时点的方差和前一时点的方差联系起来，ARCH（p）模型公式表达如下：

我们可以通过ARCH-LM检验来看数据是否存在ARCH效应，由于残差具有长期的相关性，会形成很高的移动平均阶数，所以我们引入GARCH模型，更有利于提高模型精度和参数的估计。GARCH（p，q）模型公式如下：

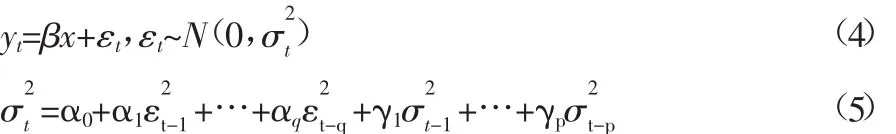
P表示异方差函数的自回归最大阶数，q是ARCH效应的最大滞后阶数。

（二）数据选取和预处理

由于股指期货合约具有到期日，为得到连续的期货合约价格，本文采用沪深300指数期货的主力合约的连续价格为期货数据，沪深300指数作为现货数据。期货的数据是从2010年4月16日至2018年6月29日，共1 995个数据；现货数据是从2005年4月8日至2018年6月29日，共3 217个数据，数据来源聚宽软件JQdata。

由于对数收益率在刻画金融市场收益率时能够很好的反映市场的波动性因素，并且可以防止剧烈波动性的干扰。所以本文采用对数收益率的形式来刻画相关指数的收益率。对数收益率计算如式6。

其中，rt为指数的收益率，Pt和Pt-1分别表示地t期和t-1期的指数收盘价，为了方便研究，下文中沪深300指数和沪深300指数期货的指数收益率分别用rhs和rif表示。

（三）协整检验

时间序列的研究中，只有模型中的变量满足平稳性要求时，传统的计量经济分析方法才是有效的。而在模型中含有非平稳时间序列式，基于传统的计量经济分析方法的估计和检验统计计量将失去通常的性质，从而推断得出的结论可能是错误的。因此，在建立模型之前有必要检验数据的平稳性。

根据数据进行做出沪深300指数期货上市以来的期现货走势图如图1所示。

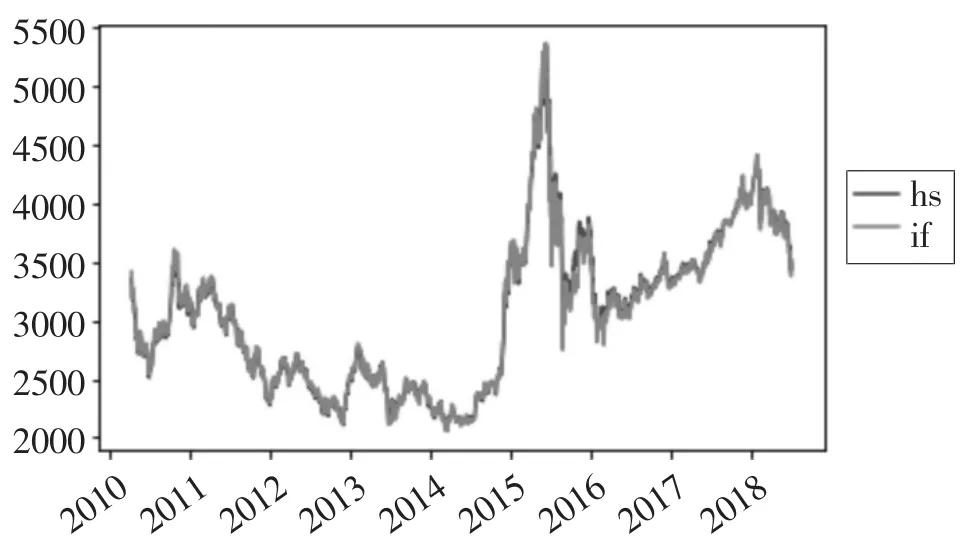
图1 沪深300股指期货和现货走势图

从图1图形可以较直观看出两者的走势具有很高的一致性和趋势性，表明期现货之间的关联性很强。此外，从图形的波动情况我们可以知道这两组数据都是非平稳的。为了检验这两组数据在2010年4月16日至2018年6月29日之间的平稳性，我们对这两组数据对数化后进行单位根检验。

从表1可以看出，在1%、5%和10%的显著性水平下，沪深300指数和沪深300期指的对数序列的ADF值都比相应显著性水平下的ADF临界值大，因此说明这两组对数序列都是非平稳序列。而对数收益率则是平稳的，说明沪深300沪指和沪深300期指的对数序列是一阶单整序列，满足协整分析条件，可以运用协整分析进一步分析它们之间的动态均衡关系。

表1 沪深300指数和沪深300期指的对数序列单位根检验结果

第一步，对沪深300股指和沪深300期指的对数序列进行OLS估计建立方程如下：

lnhs=1.007944*lnif+u R^2=0.996824

第二步，对上述方程中的残差项u进行平稳性检验，单位根检验的数值如下表所示：

表2 沪深300指数和沪深300期指的对数序列回归方程残差单位根检验结果

从表3可以看出，残差序列的ADF检验值远小于个显著性水平下的ADF临界值，所以上述回归方程的残差项u是平稳序列，所以沪深300股指和沪深300期指的对数序列之间存在协整关系。即沪深300股指和沪深300期指的之间存在着长期均衡关系。

（四）波动性分析

1.描述性统计

我们将沪深300指数按照股指期货推出与否分成两个部分，分别统计其对数收益的均值、方差等。

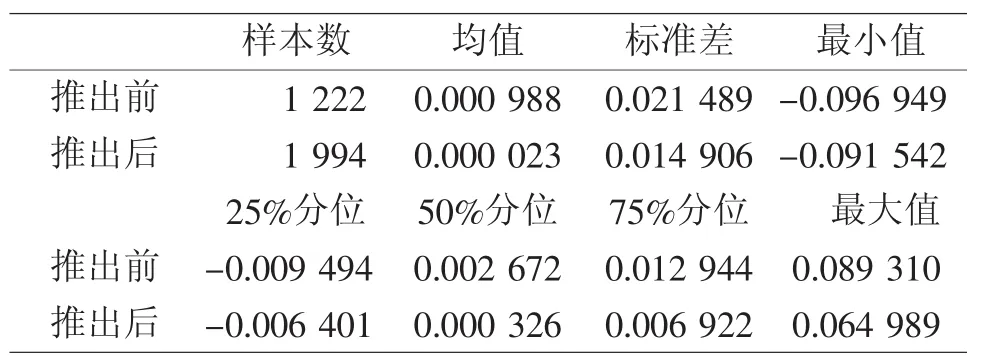
表3 股指期货推出前后沪深300对数收益率描述性统计

从表3我们可以看出推出股指期货后沪深300对数收益率的标准差大幅下降，且均值也有很大程度的下调，所以波动的变化与行情有一定关系，我们进一步建立GARCH模型分析波动性。

2.ARCH效应

根据对数收益率数据我们可以画出图2收益率波动图，从图中可以看到明显的波动聚集效应，说明对数收益率序列存在异方差性。为了说明异方差性，我们进一步进行ARCHLM检验，检验结果如表4所示。

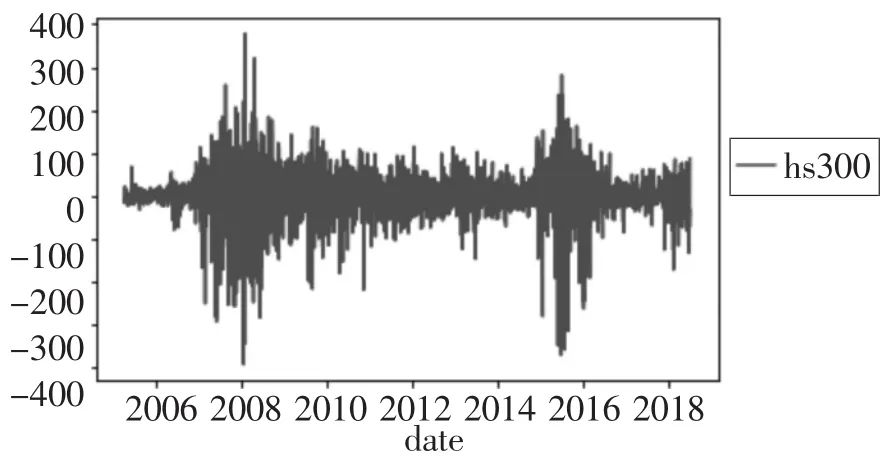
图2 沪深300指数对数收益率图

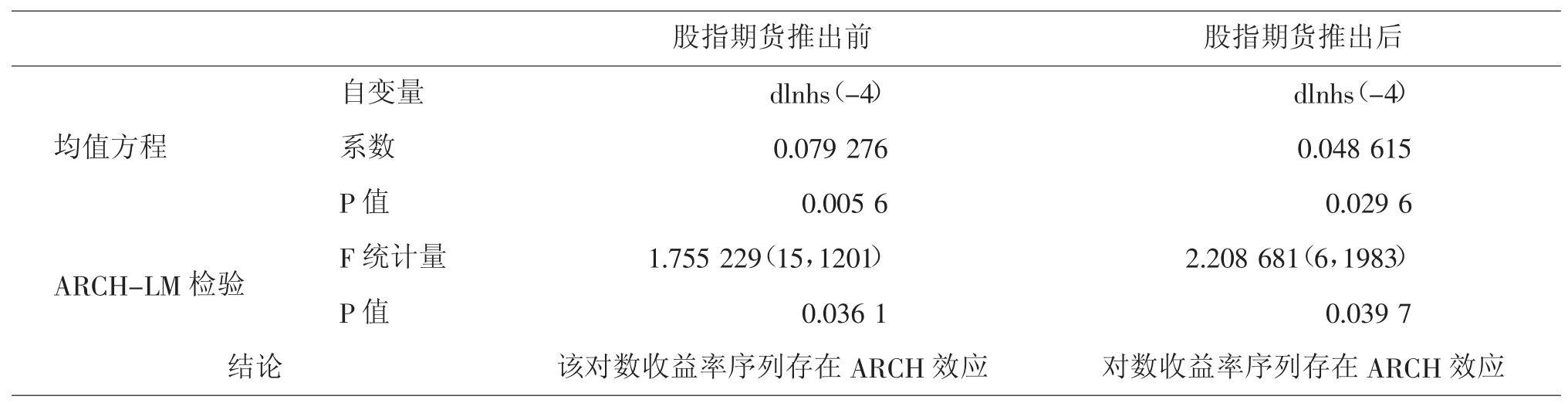
表4 沪深300指数对数收益率ARCH检验

3.GARCH模型

根据ARCH效应检验结果，我们进一步拟合序列的自回归条件异方差特性。根据AIC信息原则和模型系数的显著性我们最终选择了GARCH（4，5）模型，及如果如下表所示：

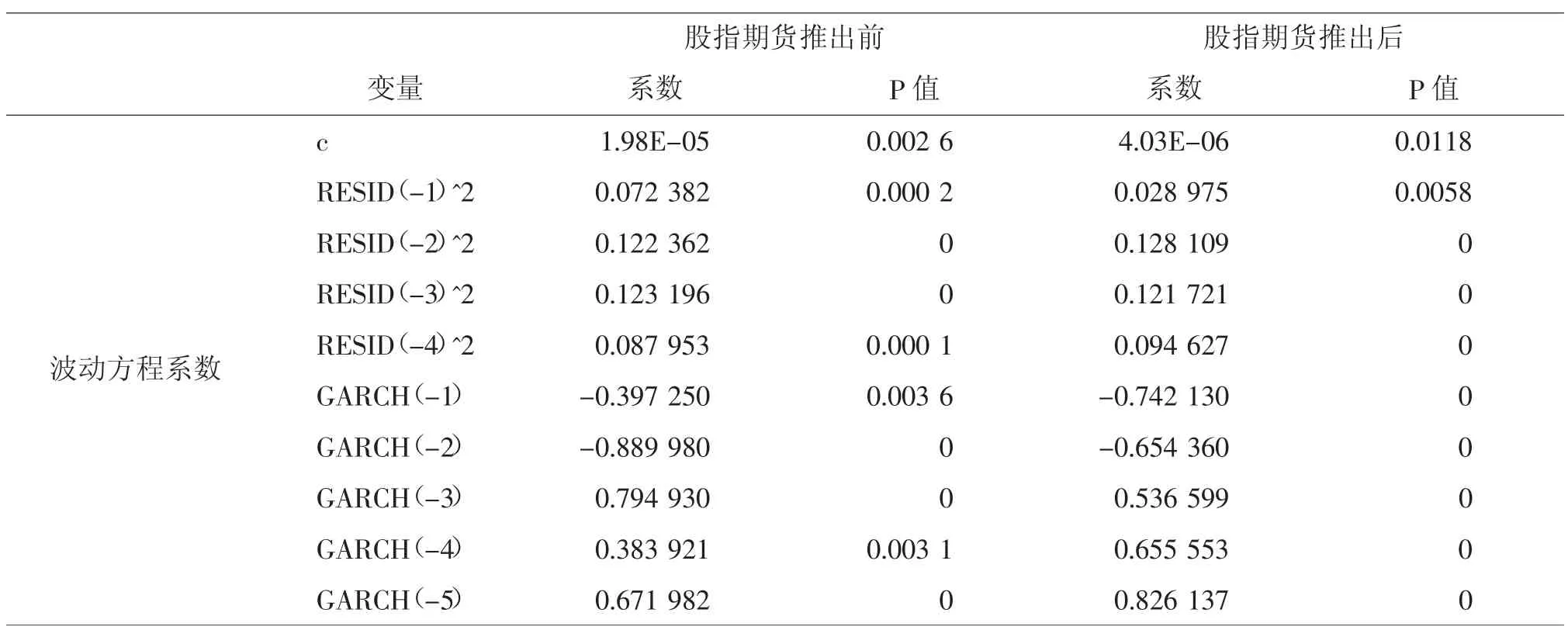
表5 沪深300指数对数收益率GARCH模型

三、结论

本文通过协整检验来检验沪深300指数期货和现货之间关联，并通过条件异方差模型来刻画股指期货推出前后沪深300指数现货的波动情况。

研究结果表明，沪深300指数期货和现货之间具有的协整关系，说明现货和期货的同涨同跌效应很明显，由于现货和期货之间有明显的长期均衡关系，我们可以进一步通过波动性分析来观察期货对现货的影响。

我国股指期货从2010年4月16号推出后，股票市场对消息的反应更加迅速，从基本统计来看，股指期货推出后，现货的均值更接近于零，标准差衡量的波动也变小了很多，最大最小值范围也有一定的缩窄，说明股指期货对现货有一定的稳定作用。GARCH模型中股指期货推出前后的系数之和分别是0.970和0.995，都非常接近于1，说明条件方差所受的冲击有一定的持久性。而且股指期货推出后的系数之和更大一些，说明股指期货推出后，市场上对消息的吸收更加平缓，而不是瞬间的冲击完成信息的消化，这样更加有利于减小市场的波动性。

沪深300股指期货并不能作为市场暴涨急跌的原因，而是对市场有一定的稳定作用，并且能为广大投资者提供风险对冲的工具。2015年股灾之后，监管者对股指期货增加了一系列苛刻的限制，在中国金融市场日益成熟的今天，希望监管者重新审视股指期货的利弊，进一步完善金融市场服务和工具，构建一个稳定的金融市场。