例谈函数值域求法
贺志雄
(德宏师范高等专科学校数学系,云南芒市 678400)
函数问题是高中数学一个非常重要的内容,其中函数值域又是一个难点,它可变式为最值问题,也可变式为不等式证明问题,其本身具有一定的综合性。函数值域求解方法灵活多样,可涉及函数与方程的转化、函数与函数的转化、函数与不等式的转化、变量与变量的换元代换、数形结合等多个知识点及思想方法。下面选择具有代表性的一个问题,从多个角度认识和解决,以体现函数值域问题求解的核心思想和方法。
例题:求函数y=的值域。
1 数形结合法
围绕数与形相互转换,初等数学中已形成了一种非常重要的数学思想方法,即数形结合的思想方法。数学家华罗庚先生曾经写过一首词,很形象地反应了数形之间的这种辩证关系:“数与形本是相倚依的,焉能分作两边飞,数缺形时少知觉,形少数时难入微,数形结合百般好,隔离分家万事非,切莫忘,几何代数统一体,永远联系,切莫分离”〔1〕25。
1.1换元基础上的数形结合法换元思想是指通过变元或式表示、代替或转换为某些确定的数学对象,将数学问题化繁为简、化难为易,从而达到化未知到已知的终极目标的一种思维倾向。换元思想的本质是映射转移,或者说就是引进某种新的映射,对原给定的函数进行分解或实施复合,它的理论依据是等量代换〔2〕。
解法1:设u=,v=,则u2+v2=1且u≥0,v≥0,该曲线方程为四分之一圆,于是问题转化为:y为何值时,直线u+v=y与该四分之一圆有交点。由图1容易得到,y的取值范围为,即为所求函数值域。

图1 解法1图列示
解法2:函数定义域为[0,1],

依照解法1可求解。
1.2不换元的数形结合法
解法3:函数的定义域为[0,1],

这里函数u=与u=-的图像分别为一段抛物线AB、CD。见图2。于是问题化归为向上平移图像CD,使其与图像AB相交至相切时,y的取值范围问题,设切点为E(x0,y0),则抛物线AB、CD在x=x0处切线斜率相等。

图2 解法3图列示
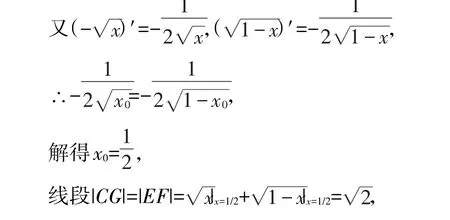
由图2易知y的范围在A点与G点之间即有1≤y≤。
1.3 构造向量的数形结合法向量作为一种带有方向的线段,集“数”“形”于一身,即向量可以类似像数那样进行运算,其本身又是一个“图形”。向量是体现数形结合方法的良好载体〔1〕111。
解法 4:设向量a=(,),b=(1,1)(见图3),


图3 解法4图列示
2 逆变法
逆变法属于一种逆向思维,它是“正难则反”思想在化归策略中的一种,简单地说,逆变法就是数学形式的反面思考,实现对立双方的转化〔3〕81。将y=f(x)看成是x的方程,若求得x=g(y),由g(y)的定义域及x的范围(原来函数y=f(x)的定义域)即g(y)的范围,则可求得y的范围。

3 判别式法
方程实质上就是求已知函数的变数值,使在变数值上已知函数有某个预先指定的值,特别是使函数值变为零,不等式也可类似地去看,于是方程和不等式都统一到函数的范畴中〔4〕161。判别式法完成了这样的一种“统一”。

消元整理后有

关于u的一元二次方程有非负解,由根与系数的关系及根存在的条件有:

4 等价转化的方法
在数学求解过程中,经常会见到“换一句话说”这样的表述形式,其实就是“构造一个等价命题”的通俗说法。简单地说,一个命题的充要条件称为它的等价命题。所谓等价转化是指通过将所解决的问题转化为它的等价命题,使得问题的条件或结论之间更趋于匀称、和谐,联系更为紧密,从而有利于解决问题〔3〕59。恒等变形是等价转化的一种方法,通过恒等变形变换问题的形式,从而使问题得以求解。

5 利用函数单调性的方法
函数的单调性,从几何直观的角度看,就是函数图像走势的变化规律〔3〕207。找到了“规律”,问题迎刃而解。
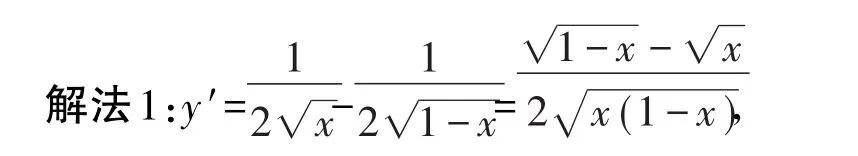
函数的定义域为[0,1],

6 三角代换法
三角代换法的基本思想,在于把函数的值域问题转化为三角函数的值域问题,在代换时,必须使三角函数的值域与被代换变量的取值范围相一致〔1〕142。消去根式是数学常用的一种划归方法,在解无理方程、无理不等式时,都要用到这种化“无理”为“有理”的方法。下面用三角函数的平方关系消去根式,得到一个三角式而不是有理式,但它产生了把一个问题得以解决的“有理行为”,这属于更广泛意义的有理化。

7 最值法
如果函数在[a,b]上连续,它的最大值和最小值分别是M和m,那么函数的值域是〔m,M〕〔4〕142。若函数y=f(x)在闭区间[a,b]上可导,最大值和最小值可从驻点的函数值及f(a)、f(b)中寻求。
解:y=x的定义域为[0,1],

通过一个函数值域问题的教学,可以引导学生对认知结构中已有的一些解法进行提炼,让学生认识到思想方法之间的联系,从而帮助学生建立起对一类问题的整体认识,进而生成处理一类问题的基本方法。这样才能让学生做到举一反三,触类旁通〔5〕。

