基于Newmark法的RV减速器传动精度计算

单丽君,孙大朋

(大连交通大学 机械工程学院，辽宁 大连 116028)*

0 引言

RV传动是由少齿差行星传动发展而来的一种新型精密传动.具有体积小、传动比范围大、运动精度高、传动平稳等一系列的优点.广泛应用于高精度机器人关节传动.德国和日本的RV减速器技术较为先进，而我国起步较晚，存在传动精度不稳定的缺陷.这种传动从产生至今已进行了大量的研究工作，在受力分析[1]、齿形优化[2]、静态性能[3]等方面的研究已达到一定的理论深度，但对其非线性动态传动精度研究文献较少，文献多是基于定值刚度和有限数量误差值的条件下建立的动态精度分析模型[4-6].而RV传动中的渐开线和摆线齿轮传动的啮合刚度和各种单项误差都是随时间变化的，是影响整机传动误差的主要因素，论文以RV-80E型号减速器为例，基于非线性理论，考虑时变啮合刚度和时变单项误差等因素，分析计算了整机的动态传动误差，研究结果对提高应用RV减速器作为关节传动的工业机器的定位精度具有重要的意义[7-8].

1 RV减速器传动原理

RV减速器是一种二级减速装置，结构紧凑，其结构如图1所示.整个减速传动装置可以归纳为两级减速部分：第一级是位于高速端的渐开线圆柱齿轮减速部分，由中心轮和两个渐开线行星轮组成；第二级是位于低速端的摆线针轮行星减速部分，由曲柄轴、摆线轮、针齿轮、针齿壳以及行星架组成.

图1 RV减速器传动系统简图

2 传动精度分析模型

2.1 动力学模型

采用质量弹簧“等价模型”的方法建立了RV减速器的动态传动精度的动力学模型，如图2所示.

图2 RV减速器动态传动精度计算的动力学模型

2.2 参变量的解释与说明

Xs、Ys为太阳轮微位移；Xpi、Ypi为第i个行星轮的微位移，(θpi-θp)为行星轮实际转角对于理论转角的微位移；ηj为第j个摆线轮的微位移，(θj-θp)、(θoj-θc)为摆线轮实际自转角和共转角对于理论转角的微位移；Xca、Yca为行星架微位移，(θca-θc)为行星架转角对于理论转角的微位移.

输入轴扭转刚度为Ks，太阳轮与行星轮间的轮齿啮合刚度为Ki，曲柄轴与摆线轮轴孔的转臂轴承刚度为Kj、曲柄轴和行星架轴孔的支撑轴承刚度为Kb、摆线轮与针齿间的轮齿啮合刚度系数为Kjk，轴承间隙为δbji，针齿的直径误差引起的间隙为δjb；以及摆线轮轮齿的齿形误差δb.

以向量的方式表示误差，意为大小和方向.太阳轮、行星轮基圆的偏心误差(Esβs)、(Epiβpi)在其啮合作用线上产生的位移：

esi=Escos(θs+βs-Ai)

(1)

epi=Epicos(βpi-θp-Ai)

(2)

Ai=θc+φi+π/2-α

(3)

式中,α为太阳轮和行星轮的啮合角(°).

太阳轮装配误差(Asγs)引起的微位移：

δsx=Ascosγs

(4)

δsy=Assinγs

(5)

针轮和摆线轮的齿槽偏差Rk、Rjk，圆周方向上的齿距累计偏差Pk、Rjk引起的微位移：

δRk=-Rkcos(αjk-φjk)

(6)

δRjk=Rjkcos(αjk-φdjk)

(7)

δPk=-Pkcos(αjk-φjk)

(8)

δPjk=Pjkcos(αjk-φdjk)

(9)

摆线轮上的均布孔的偏心误差(Ejiβji)以及曲柄轴上偏心距(Eqjiβqji)引起的微位移：

δxji=-Ejicos(θc+φi+βji)

(10)

δyji=-Ejisin(θc+φi+βji)

(11)

δqxji=-Eqjicos(θp+φj+βqji)

(12)

δqyji=-Eqjisin(θp+φj+βqji)

(13)

行星架支撑曲柄轴的偏心误差(Eciβci)以及行星架装配误差(Acγc)引起的微位移：

δcxi=-Ecicos(θc+φi+βci)

(14)

δcyi=-Ecisin(θc+φi+βci)

(15)

δcx=Accosγc

(16)

δcy=Acsinγc

(17)

2.3 RV减速器动态传动精度的动力学方程

通过对机构间零部件的受力分析，推导出RV减速器的动力学方程，如式(18)～(28).

(18)

(19)

(20)

(21)

(22)

(23)

(24)

(25)

(26)

(27)

(28)

通过求解上述方程组，在求得实际输出转角θca，进而求出它的传动误差Δθca.

3 RV减速器运动学方程的求解

所建立的RV减速器动态传动精度计算模型属于非线性动力学模型，采用非线性Newmark法[9-10]对其进行求解.

(29)

通过Newmark法假设的t+Δt时刻的速度和位移为:

(30)

(31)

参数γ和β的选择对算法影响较大.算法稳定性分析指出，当γ≥0.5，β≥(1/2+γ)2/4时，Newmark法无条件稳定，这时可以只根据精度的要求选择时间步长Δt.

计算步骤如下：

(1)初始计算

①建立刚度K，质量矩阵M和阻尼矩阵C.

③选择时间步长Δt以及参数γ和β，并计算下列有关常数.

④计算有效刚度矩阵

=K+α0M+α1C

(32)

(2)对每个时间步计算

①计算t+Δt时刻的有效载荷向量

(33)

②求t+Δt时刻的位移

(34)

③计算t+Δt时刻的加速度和速度

(35)

(36)

4 数值仿真

以RV-80E为例，初始参数如表1所示.

表1 RV减速器基本结构参数表

其中，针齿与齿槽间的间隙δjk=0.005 mm；摆线轮曲柄轴孔处的轴承间隙δbji=0.001 5 mm；行星架上曲柄轴孔处的轴承间隙δxi=0；行星架与壳体间的轴承间隙δca=0；其他误差初始值设定如表2、3、4所示.

表2 摆线轮曲柄轴孔偏心误差参数

表3 曲柄轴偏心轮偏心误差参数

表 4 行星轮曲柄轴孔偏心误差及装配误差参数

基本参数以及零件误差根据实际测量的资料所得，对所建立的动力学方程求解并进行数值仿真，传动误差随行星架理论输出转角变化的仿真曲线如图3所示，传动误差在第二周趋于稳定.系统传动误差曲线具有清晰的波动性，传动误差的范围为：-42.52″～8.141″，正值表明输出值实际值大于理论值，负值意为输出值实际值小于理论值.曲线呈现正负交替，表明RV减速器工作中齿轮啮合存在快慢差异，传动过程不平稳.

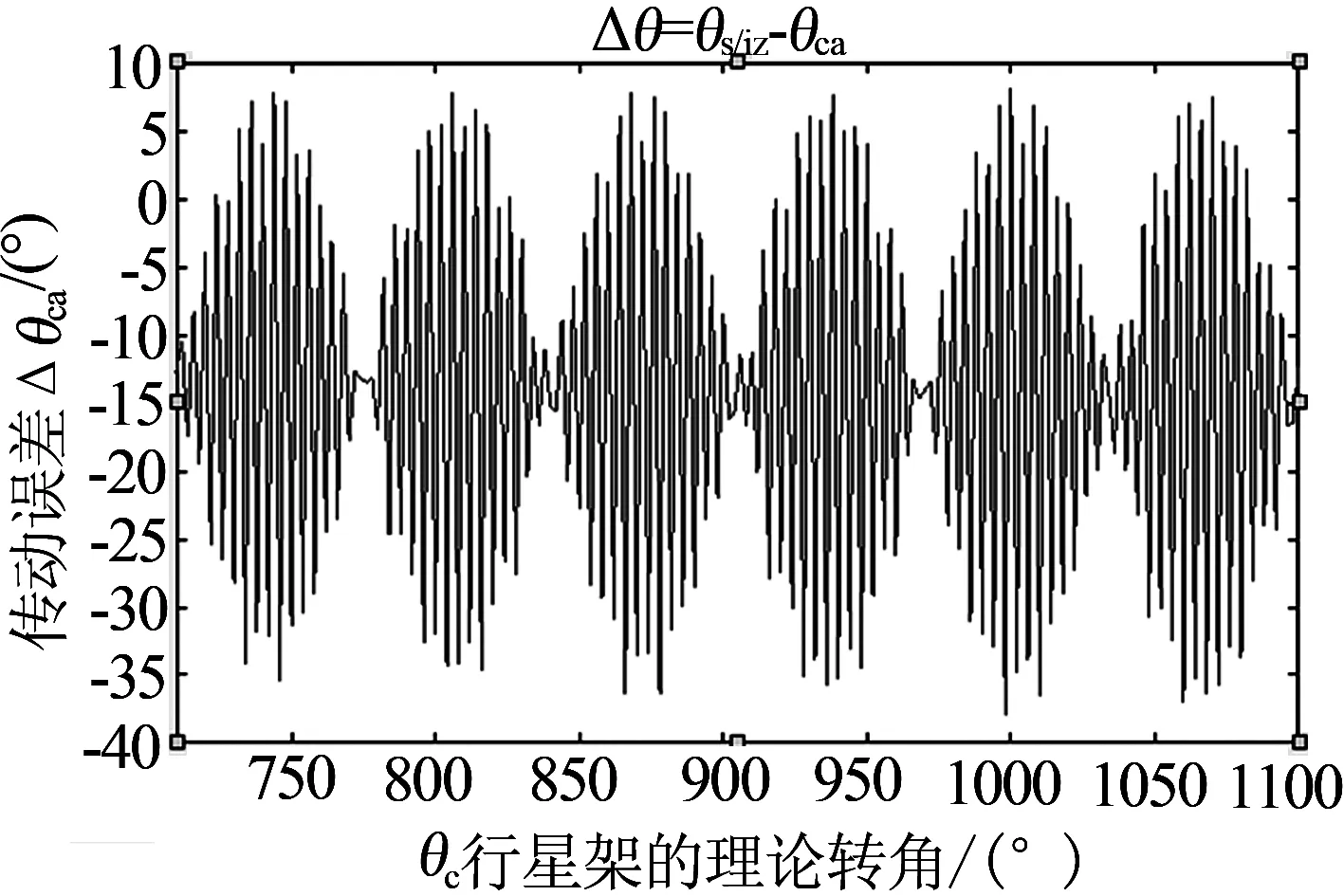
图3 系统传动误差动态曲线

5 结论

(1)采用质量弹簧“等价模型”方法建立动力学分析模型；根据动力学模型推导方程，并采用Newmark法通过Matlab编程对方程进行求解；

(2)计算结果表明，最大误差为42.52″，在1′以内.传动误差呈现大周期和小周期变化，其中大周期和小周期分别由摆线轮转一圈和一个齿引起输出轴的转角误差导致的；为研究单项误差对RV减速器传动的影响做了准备.