BP及RBF神经网络铝合金车体焊接残余应力预测

马思群，刘选，金辉，冯良波，聂春戈,刘寒

( 1.大连交通大学 机车车辆工程学院， 辽宁 大连 116028; 2.中车长春轨道客车股份有限公司 国家工程研究中心车体研发部,吉林 长春 130062; 3.中车长春轨道客车股份有限公司 工程技术部,吉林 长春 130062)*

0 引言

在高速列车车体焊接制造工艺过程中，选择合适的焊接工艺参数尤为重要.如果焊接工艺参数选择不合适，高速列车车体侧墙会存在较大的焊接残余应力，无疑对交通及旅客人身安全带来非常大的隐患[1-2].

通过试验获得较为合适的焊接工艺参数的方法费用昂贵.通过数值仿真来选择焊接工艺参数的方法耗时较长,无法满足短时间内对焊接工艺参数选择要求.

人工神经网络可通过学习，实现不同焊接工艺参数下焊接残余应力快速预测[3].

针对神经网络需要的样本较多，试验费用昂贵问题，可利用由焊接数值仿真软件(SYSWELD)获得的仿真数据，建立并训练BP和RBF神经网络对焊接残余应力快速预测.研究成果为企业提供更经济、更有效率的焊接工艺参数选择方法以及理论依据.

1 焊接残余应力仿真计算

1.1 仿真计算可行性验证

为了验证数值模拟的准确性，通过射线法对焊接试件焊接残余应力进行测试，其中X射线法的测量原理：金属材料的晶格中的晶面间距是一定的，当射线射入金属点阵后将发生衍射现象，其衍射角同晶面间距成布拉格关系.当由应力引起晶面间距变化后，衍射角也发生变化.射线仪器可以准确地测定出衍射角的变化，从而根据弹性力学方程计算出应力大小.

对试件分别进行利用焊接数值仿真软件(SYSWELD)计算和试验测试，焊接的工艺参数和数值仿真参数相同.试件几何尺寸为长500 m×宽200 mm×厚4 mm的铝合金(材料为6005)平板，实验方法为MIG 焊，焊接接头开70°坡口.

从距起始点50 mm处开始沿着焊缝方向每隔50 mm选取九个测试点.

1.2 计算结果与实验结果比较

由图1发现仿真结果和实验结果的分布规律基本一致，在数值上存在一定误差，产生误差的原因可能为：

(1)数值模拟采用的是软件自带材料库中的材料属性与实际材料属性有所差别；

(2)受测量仪器、焊件表面状态以及人为操作等因素的影响都会对测量造成误差.

图1 计算结果与实验结果对比

通过对实验结果与数值仿真结果对比发现两者吻合良好，证明了利用SYSWELD软件预测焊接残余应力方法的可行性.

因神经网络需要的样本较多，考虑到试验费用问题，无法通过试验获得.则利用数值仿真方法获取足够的样本.

1.3 模型介绍

高速列车车体侧墙主要由窗上板、上墙板、窗间板、窗下板和下墙板等铝合金型材焊接而成.

以某型高速列车铝合金车体4 mm厚侧墙为例，划分有限元网格.有限元模型及其侧墙焊缝分布如图2所示.

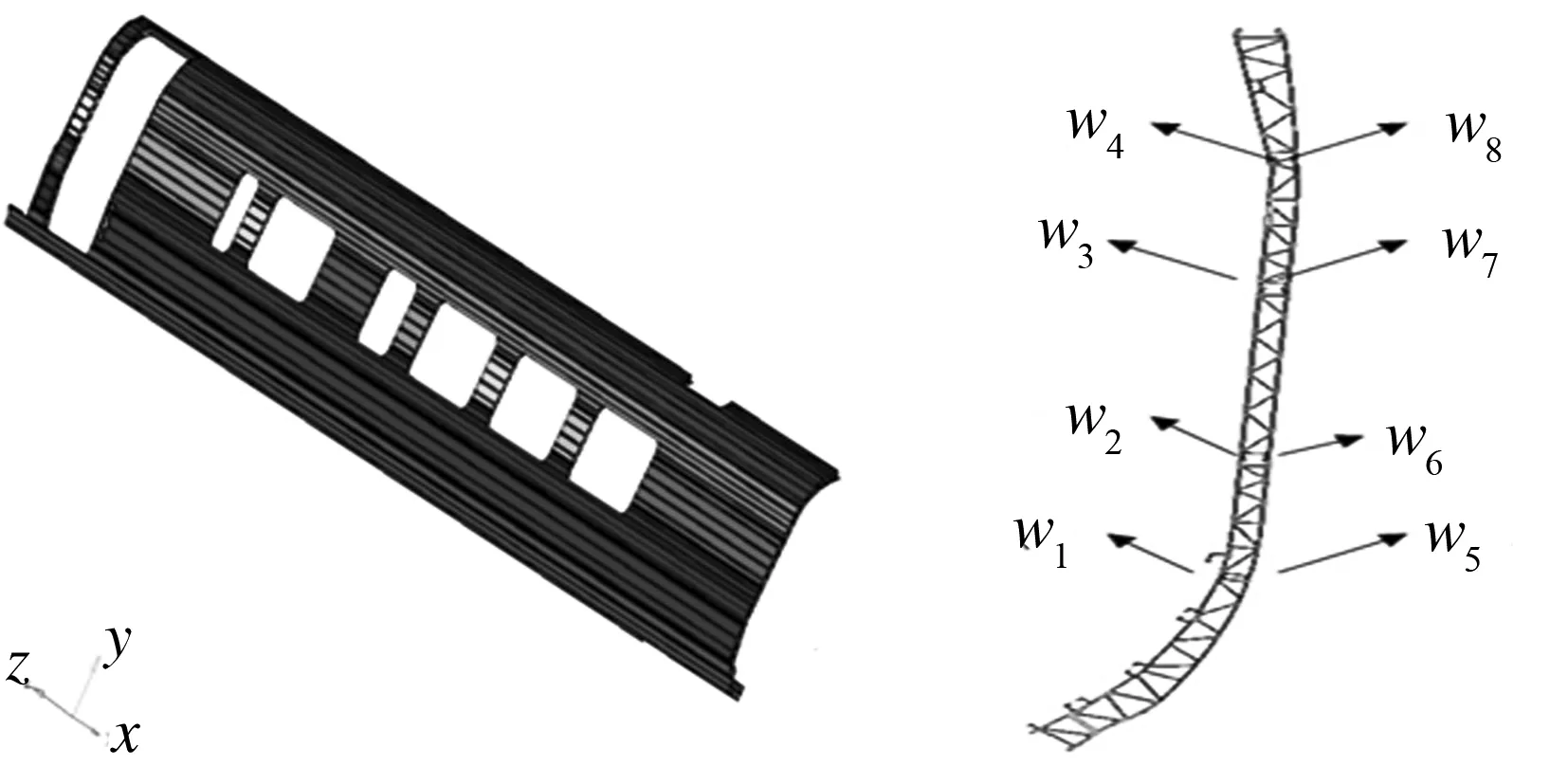
(a) (b)

图2(b)中W1～W8分别表示第一～第八道焊缝.焊接工艺如下：在焊前提供100℃初始预热温度，按照由内及外、从低到高的焊接顺序依次焊接(即W1～W4，W5～W8)，焊完一道需要一段冷却时间，冷却到50～100℃时再对下一道焊缝进行焊接.

1.4 热源校核及仿真计算

以双椭球热源作为热源模型，将热源模型分为前后两个1/4椭球体.

假设ff、fr为前后椭球的热量输入，可以得出前后椭球的热流分布为：

(1)

(2)

前半部分的热输入为：

(3)

对于后半部分同理为:

(4)

式中,af、ar、bh和ch为热源参数，bh影响熔宽，ch影响熔深，ar、af确定需要一定的经验同时也是非常耗时.

将最终焊接热源模型与真实焊接切片断面形状对比，其吻合效果较好，如图3所示.

图3 热源模型与真实切片对比

考虑到车体侧墙横向焊接残余应力较纵向焊接残余应力而言较小，因此引起焊接残余应力的主要因素就是纵向收缩.

重点研究侧墙的纵向焊接残余应力.在预热温度为100℃下，选择15组不同焊接工艺参数，利用校核好的双椭球热源模型，对侧墙8道焊缝进行仿真计算，经试验验证仿真计算结果可靠.工艺参数及结果如表1所示.

表1工艺参数及各条焊缝最大焊接残余应力计算结果

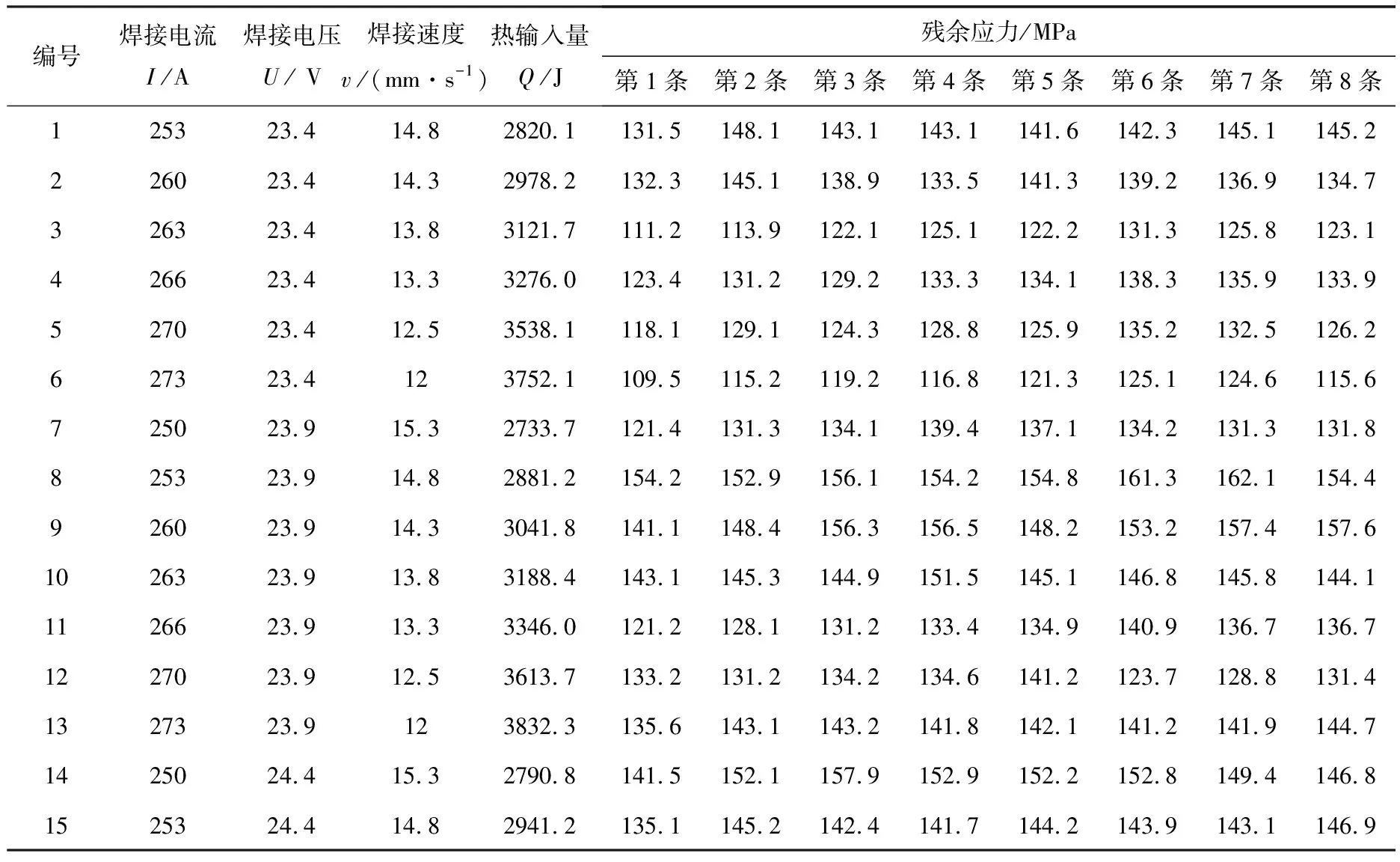
编号焊接电流I/A焊接电压U/ V焊接速度v/(mm·s-1)热输入量Q/J残余应力/MPa第1条第2条第3条第4条第5条第6条第7条第8条125323.414.82820.1131.5148.1143.1143.1141.6142.3145.1145.2226023.414.32978.2132.3145.1138.9133.5141.3139.2136.9134.7326323.413.83121.7111.2113.9122.1125.1122.2131.3125.8123.1426623.413.33276.0123.4131.2129.2133.3134.1138.3135.9133.9527023.412.53538.1118.1129.1124.3128.8125.9135.2132.5126.2627323.4123752.1109.5115.2119.2116.8121.3125.1124.6115.6725023.915.32733.7121.4131.3134.1139.4137.1134.2131.3131.8825323.914.82881.2154.2152.9156.1154.2154.8161.3162.1154.4926023.914.33041.8141.1148.4156.3156.5148.2153.2157.4157.61026323.913.83188.4143.1145.3144.9151.5145.1146.8145.8144.11126623.913.33346.0121.2128.1131.2133.4134.9140.9136.7136.71227023.912.53613.7133.2131.2134.2134.6141.2123.7128.8131.41327323.9123832.3135.6143.1143.2141.8142.1141.2141.9144.71425024.415.32790.8141.5152.1157.9152.9152.2152.8149.4146.81525324.414.82941.2135.1145.2142.4141.7144.2143.9143.1146.9

2 神经网络预测

人工神经网络具有自组织、自学习、任意逼近连续函数等能力[5].侧墙8条焊缝间距较小，会存在热源耦合分布，需将焊接预热温度作为神经网络的一个输入参数.将最大纵向焊接残余应力作为神经网络的单一输出.创建焊接电压、焊接电流、焊接速度以及预热温度与最大纵向焊接残余应力的BP、RBF神经网络预测模型，初步神经网络结构如图4所示.

图4 神经网络结构图

2.1 BP神经网络模型确定

通常BP神经网络中隐层节点个数有两种确定方法：一是试凑法；二是首先选择较多个隐节点，采用误差代价函数逐渐减小影响小的权值，当权值减小的零时，就去掉了相应的节点.

方法一中经验公式有：

(5)

n=log2m

(6)

(7)

式中,n为隐层节点数，m为输入层节点数，l是输出层节点数，α为1～10间的常数.

方法二中误差代价函数为：

(8)

式中,ε表示训练误差，ω为权值，E总是输出误差平方和，h为隐层个数.

由误差代价函数法确定隐层节点个数为6，已知输入参量为4个(即焊接电压、焊接电流、焊接速度以及预热温度)，输出参量为1个(即最大纵向焊接残余应力)，则将结构模型确定为4∶6∶1.

2.2 BP神经网络训练

因BP神经网络算法存在一定工程缺陷，现对其适当改进.增加一个考虑前后两次权值变化的调整作用的动量项.其公式为：

ΔW(t)=αβX+γΔW(t-1)

(9)

式中，W表示的是权矩阵，X表示的是输入向量，而γ表示的是动量系数，γ位于0～1之间的小数，α表示学习率，β表示输出误差信号，取动量系数mc=0.85.

初始学习率α选定为0.1，logsig对数S型函数作为传递函数[6]，训练精度(goal)的值选定为0.0001，选定最大迭代次数(epoch)为1000次，动量系数(mc)的值选定为0.95.

训练函数选定为trainlm函数，将输出结果进行反归一化处理，最后进行输出.

2.3 RBF神经网络模型确定

由于RBF神经网络容易太尖或太平，所以可将RBF神经网络通过公式设定，设定公式为：

(10)

式中，dmax表示的是样本间最远距离，P表示的是样本数目.

确定输出层权值方法一般选择最小均方算法(LMS)理论，其数学公式为：

(11)

ΔW的各分量为:

(12)

由正则化径向基函数理论，可知神经网络的隐层节点个数与输入节点数相等，则RBF神经网络的结构就可以确定为4∶4∶1.

2.4 RBF神经网络训练

goal、MN、spread、DF取默认值，高斯函数作为扩展函数[7]，Radbas函数作为隐层激励函数，Dist函数作为加权函数，Purelin作为输出层激励函数，结果反归一化处理[8].

以焊接仿真前10组不同焊接工艺参数及对应的最大纵向焊接残余应力值作为训练数据，后5组作为预测数据.

3 结果分析

对焊缝的仿真结果(即FEM结果)、BP网络预测结果、RBF网络预测结果进行比较分析.横坐标为样本编号，样本编号1、2、3、4、5表示第一条焊缝， 样本编号6、7、8、9、10表示第二条焊缝，样本编号11、12、13、14、15表示第三条焊缝，样本编号16、17、18、19、20表示第四条焊缝，纵坐标为最大纵向焊接残余应力，如图5所示.

由图5可以看出，样本编号为12(即第三条焊缝)的BP神经网络的平均误差为6.7%.样本编号为12(即第三条焊缝)的RBF神经网络的平均误差为6.8%.

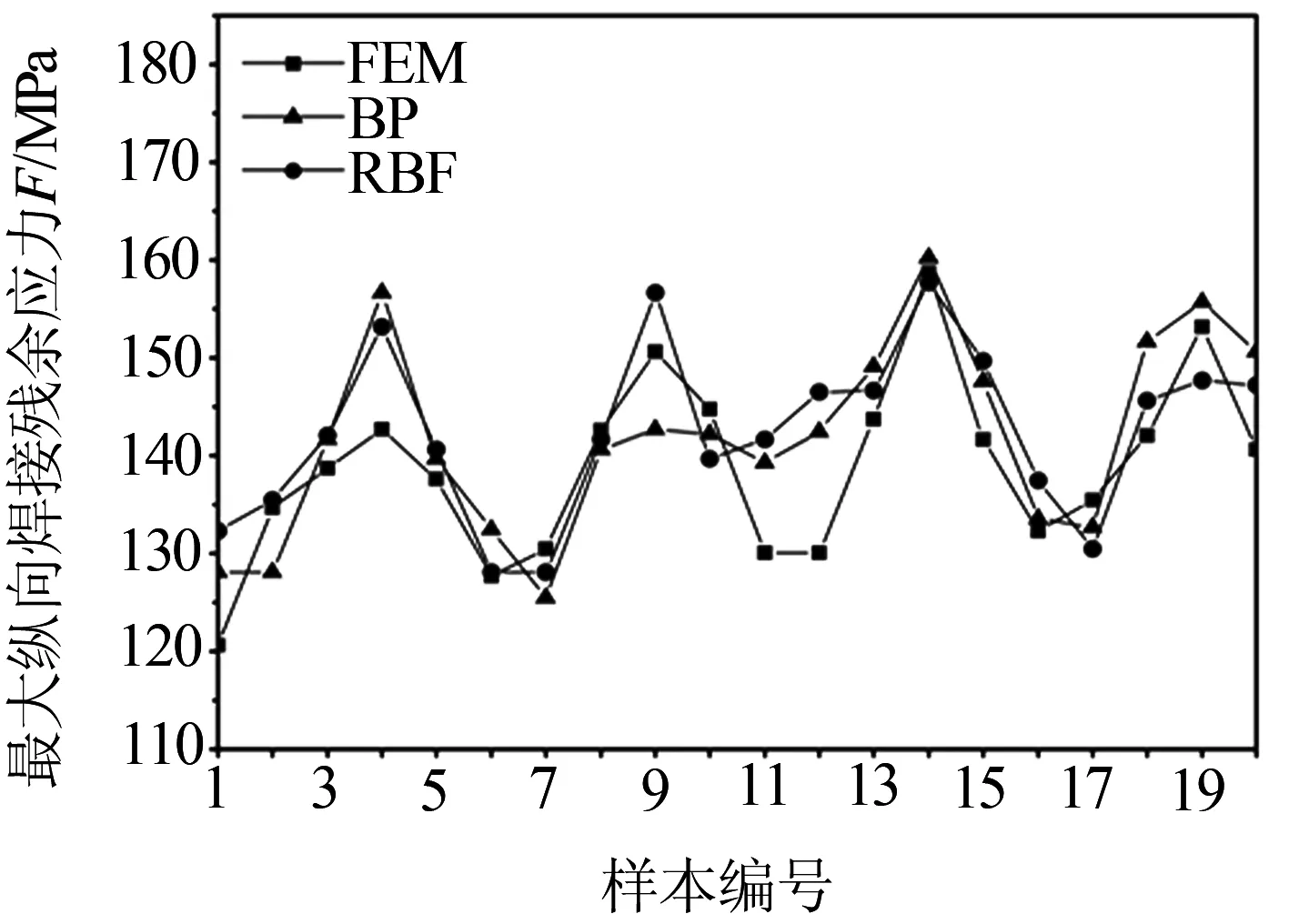
图5 预测值与仿真值对比

图6中横坐标中样本编号1、2、3、4、5表示第五条焊缝，样本编号6、7、8、9、10表示第六条焊缝，样本编号11、12、13、14、15表示第七条焊缝，样本编号16、17、18、19、20表示第八条焊缝.

图6 预测值与仿真值对比

由图6可以看出，样本编号为19(即第八条焊缝)的BP神经网络的平均误差为5.8%.样本编号为17(即第八条焊缝)的RBF神经网络的平均误差为7.8%.

因此，BP网络和RBF网络都能够对不同焊接工艺参数下的焊接残余应力值进行较好的预测，平均误差在8%以下.

4 结论

(1)针对神经网络所需输入-输出样本数据较多，试验费用昂贵问题，首先试验验证焊接数值仿真软件(SYSWELD)仿真计算的可行性，然后对某型号高速列车铝合金车体侧墙8道焊缝侧墙进行数值仿真计算.利用仿真数据作为样本数据;

(2)利用前10组仿真数据作为输入-输出数据，创建并且训练BP、RBF神经网络模型，然后对后5组仿真数据进行预测;

(3)预测值与仿真值比较显示，BP网络和RBF网络都能够对不同焊接工艺参数下的焊接残余应力值进行较好的预测，平均误差在8%以下.增加网络训练样本数据，精确度还可进一步提高.研究成果可为企业快速选择合理的焊接工艺参数，起指导作用.