禁止拖期交付的无等待流水车间调度问题算法研究
宋存利
( 大连交通大学 软件学院, 辽宁 大连 116028)*
0 引言
无等待流水车间调度问题是一种典型的生产车间调度问题,在炼钢、食品生产、化工、机械等行业有广泛的应用背景.用Graham等人[1]的三参数表示法表示该问题为F|nwt|Cmax.文献[2]已经证明在设备数量大于等于3时为NP难题.针对此问题大量的学者对其进行了研究.宋存利等[3]在总结该问题特性的基础上,提出了求解大规模无等待流水车间的迭代邻域搜索算法;潘全科等[4]提出了一种通过延长工序加工时间进一步改进调度方案的离散的粒子群算法;Aldowaisan等[5]提出了一种高效的模拟退火和遗传算法;Ventura[6]提出了禁忌搜索算法.以最小化总流水时间为研究目标的文献有:Sapkal等[7]提出了一种启发式算法,该算法以工件在瓶颈设备上的加工时间和来初始化初始解,实验证明该算法的有效性.文献[8]提出了一种遗传算法,文献[9]提了模拟退火算法,文献[10]提出人工免疫系统.以上这些文献的共同点是都没有考虑工件的交货期.文献[11-13]考虑了车间调度问题的交货期限,但是以最小的提前或延迟代价为目标,也就是说交货期不是严格的约束,允许以最小代价超出交货期限.而以严禁拖期交付且最小化完工时间为目标的文献鲜见相关报道.基于此,本文研究了禁止拖期交付的无等待流水车间调度问题,研究目标是在满足约束条件的基础上使得加工时间makespan达到最小,提出了求解该问题的基于有向图搜索的精确算法ESA和基于ESA的分段迭代搜索算法SISA-ESA.
1 问题描述及建模
禁止拖期交付的无等待流水车间调度(no-wait flow shop scheduling即NWFS)问题可表示为F|nwt,Ti|Cmax,也就是n个带有严格交货日期的工件在m台设备上加工,每个工件在每台设备上都有相应的加工工序及加工时间要求,且每个工件流经设备的加工顺序相同.一个工件一旦进入到加工流程,必须保证从第一道工序到最后一道工序连续加工,中间不能停顿,不能被抢占.一台设备在同一时间只能加工一个工件,并且每一个工件都必须在交货期前完成加工.本文要研究的目标是寻找一个调度序列π,使得所有工件都在其交货期内完工且完工时间makespan达到最小化.为方便问题描述,定义数学符号如下:
n:待加工工件的个数
m:加工设备的数量
Ji:代表第i个工件,i为工件序号
Ti:代表工件Ji的交货期限
Ci:代表工件Ji的完工时间
Si,j:代表工件Ji在设备Mj的加工开始时间
Pi,j:代表工件Ji在设备Mj上的加工时间
Di,k:当工件Ji的直接后继加工工件是Jk时,工件Jk与工件Ji的最小完工时间距离差.
为了讨论问题方便,在调度序列π之前插入了一个虚拟工件J0.
定义决策变量Xi,j:
(1)
问题目标:
Cmax=min{max{Ci|i=1,2,…,n}}
(2)
s.t.
Ci=Si,m+Pi,m
(3)
Si,j+1=Si,j+Pi,j
(4)
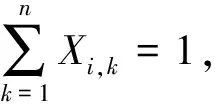
(5)
Xi,k+Xk,i≤1, 其中i,k=1,2,…,n
(6)
(7)
Xi,i=0, 其中i=0,1,2,…,n
(8)
Si,1≥0
(9)
Ci≤Ti
(10)
(11)[3]
对上述公式的解释如下:式(1)的取值确定了一个调度序列,式(2)为本问题的目标函数;式(3)提供了每个工件的完工时间计算方式;式(4)约定了每个工件的后一道工序必须在其前一道工序完工后立即加工,即实现无等待;式(5)约定了在一个调度序列中,每个工件只能有一个直接前驱工件;式(6)~(8)约定一个给定调度工件的直接前驱关系;式(9)说明每个工件的最早开工时间为0;式(10)约定每个工件的完工时间必须小于交货期;式(11)描述两相邻工件的最小完工时间距离[3],即工件Jk在工件Ji紧后加工,则工件Jk最快在工件Ji完工之后过Di,k时间完工.目标函数的计算如式(12)所示:
(12)
根据式(11),由于两工件的最小完工时间距离和两对应工件的加工时间有关,因此可事先计算出来,形成最小完工时间距离矩阵D.
(13)
2 问题的图形化表示及搜索算法
2.1 图形化表示
定义NWFS的有向无环图G={V,E},其中V代表结点,在图G中共有n×n+1个结点,每个结点对应一个工件,图G的结点共有n+1列,除第0列只有一个虚拟结点0外,其他n列每列都有n个结点,用工件J1,J2,…,Jn表示.E代表两结点之间的一条有向边.第0列虚拟结点J0到第一列的每个结点共发出n条有向边.第1列到第n-1列节点只向下一列不同节点发出有向边,因此每个节点发出n-1条有向边,最后一列节点不发出有向边,边的权值为Di,j.问题的实质就是从有向图G中找到一条从虚拟结点出发,经过每列一个结点且仅一个,且经过不同列上的的结点编号不能相同的一条最短路径.
具体以4工件的加工为例,形成的有向无环图共有5列结点,第0列只有虚拟结点J0,第1列到第4列每列都有4个结点,依次为(J1,J2,…,J4),如图1所示,图2为其中一条加工路径实例.

图1 由4个工件形成的有向无环图

图2 加工路径实例
2.2 问题性质特点
性质1:在F/nwt,Ti/Cmax问题,对任意一个工件Ji,其最早的完工时间为Ci=D0,i,若其最早完工时间D0,i>Ti,则此调度任务无解.证明略.
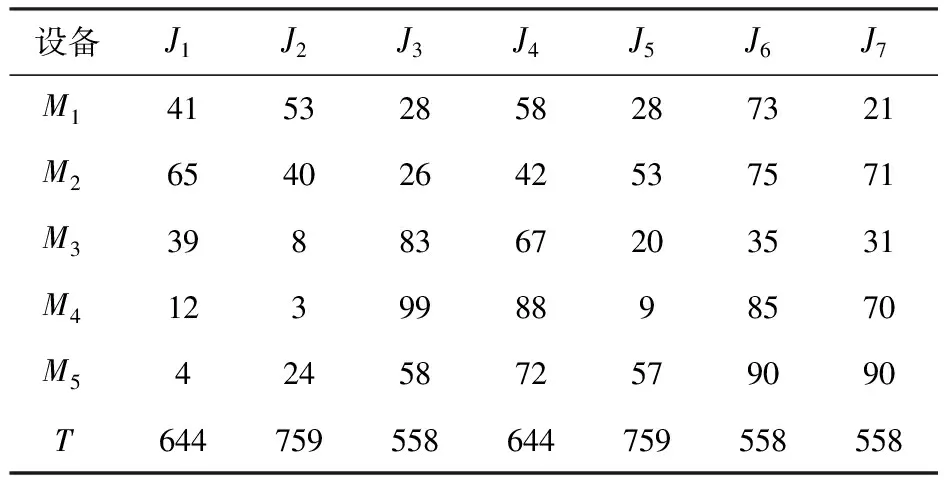
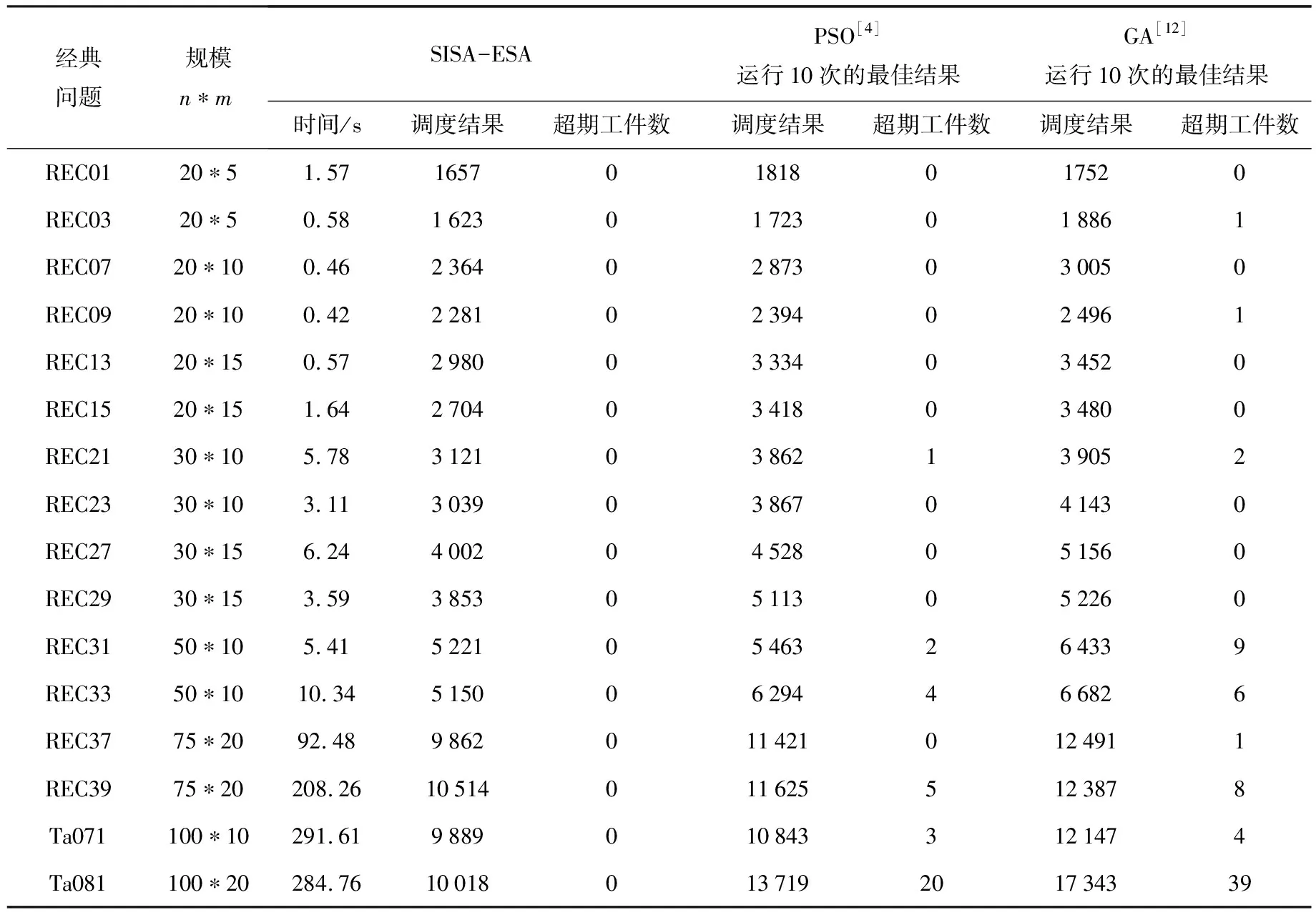
性质2:根据文献[4]主动调度的概念,F/nwt,Ti/Cmax问题的优化解一定是一个主动调度,因此若给定一个主动调度,他包括的调度序列有(Ji,…,Jk,…,Jq,…),则一定有Di,k 性质3:在F/nwt,Ti/Cmax问题中,给定一个满足交货期要求的部分调度π′,若将工件Jk安排在π′之后加工时,有Ck>Tk,即不满足Jk的交货期约束,则工件Jk在部分调度π′的其他任何一个后续位置进行加工都会有Ck>Tk成立;则在图G中没有必要继续沿着π′这条路探索下去.证明略. 针对图G,提出精确搜索算法(ESA)如下: 步骤1:计算工件之间的最小完工时间距离矩阵D. 步骤2:定义数组A[n],用来记录每一列结点的探测位置.其初始值为1,定义变量j为当前要探测的列号,令j=1,定义变量i,令i=1,代表第j列第一个结点的位置,定义部分调度序列P={0};定义变量num,令num=1定义,代表部分调度P的结点的个数;Cmax为最小化的最大完工时间,令Cmax=M,M无限大,定义Pbest为最好的调度,初始值为φ. 步骤3:首先从虚拟结点0出发,分别访问第一列中的所有结点Vi,1,计算每个结点的完工时间Ci=D0,i,若存在结点Vi,1,其完工时间Ci>Ti,则根据性质1,此问题无可行解,算法终止.否则结点V1,1进入到调度序列P中,P={0,V1,1},num=num+1,A(j)=1,j=j+1,i=1,转步骤4. 步骤4:从位置i探测第j列中还没有进入到部分调度P中的所有结点Vi,j,计算结点Vi,j的完工时间,若存在CVi,j>TVi,j或CVi,j>Cmax,则根据性质3和性质2,放弃后续探测,删除部分调度P中的最后一个结点Pnum,转步骤5,否则,转步骤6. 步骤5:令num=num-1,j=j-1,i=A(j)+1,判断num≥0是否成立,成立则判断i是否大于n,是则转步骤5,否则转步骤6;否则说明num小于0,则转步骤7. 步骤6:在第j列中,从第i行开始探测没有在部分序列P中的结点,假如发现的第一个结点为Vi,j,则该结点进入部分调度序列P中,同时令A(j)=i,num=num+1,j=j+1,i=1,如果 num=num+1, 则令Pbest=Pi,Cmax=Cpinum,同时令 num=num-2,j=j-2,i=A(j)+1,转步骤6,否则转步骤4.如果没有发现满足条件的结点,则删除P中的最后一个结点,转步骤 5. 步骤7: 若Pbest不为空,则输出结果Pbest和Cmax,否则无解. 考虑到大规模的F|nwt,Ti|Cmax问题,ESA的CPU运行时间将不可忍受,因此提出一种基于ESA的邻域迭代搜索算法SISA-ESA.算法思想是,对工件按照其交货日期由小到大排成队列Line,随机选择分段长短L,其中8≤L≤11,对队列Line按长度L依次分段,对每段工件依次采用ESA算法搜索满足工期约束的最短路径,若第一段出现不能满足工期约束的最短路径,则算法结束,输出无解.否则,按照最短路径调整该分段的工件排序.对其他后续分段,在其前一分段调度结果的基础上分别执行ESA并相应调整期排序顺序.若出现某一工件在相应分段无法满足其工期要求,则将其插入到前面分段的最后一个工件之前做判断,若不满足交货期,继续前移,直到满足条件或最终输出无解.迭代该算法,直到满足迭代终止条件为止. 为了说明算法的有效性,本文算法使用VC++编写,计算机内存为2GB,处理器为Q8400M2.66GHz,操作系统采用WIN7.本文首先对文献[3]的案例进行ESA算法实验,即7个工件在5台设备上的无等待流水车间调度问题,相应的工件的加工时间及交货日期(交货期转换成了具体的单位加工工时)如表1所示.表2中,EF代表对已知交货日期的放大倍数,共设置了6组不同的放大倍数,RT代表算法ESA的运行时间,P为对应的调度序列,Cmax为最小化的最大完工时间.实验结果见表2所示. 表17个工件在5台设备上的加工时间表 设备 J1J2J3J4J5J6J7M141532858287321M265402642537571M33988367203531M4123998898570M54245872579090T644759558644759558558 表2 带有不同交货期约束的 从结果可以看出,当已知的交货日期缩小到0.8倍时,则问题不存在满足交货日期的可行解,实验2、实验3和实验4的结果可看出随着交货日期约束的放松,ESA的寻优结果越来越好.当放大到一定值后,ESA找到的是该问题的全局最优解,如实验4-6.对于该问题,当EF=1.2时,每个工件的交货日期均大于全局最优解,所以肯定能找到问题的全局最优解了. 表3中的实验数据取自国际benchmark案例,当m=5时,取REC01前n个工件的加工数据;m=10时,取REC07的前n个工件的加工数据;m=20时,取REC37的前n个工件的加工数据. 表3 带有交货期约束的无等待流水调度问题调度结果 表4以国际benchmark的无等待流水调度问题为例,交货日期生成方式和表3采用同一种算法.为了说明本文算法的有效性,又由于以严禁拖期为目标的算法还没发现,因此采用PSO[4]算法和GA[12]算法的运行结果与本文算法进行比较,在此将PSO与GA算法的目标函数改为满足交货期约束工件个数最大为目标,算法参数采用文献自身参数设置.同时设置SISA-ESA的最大迭代代数为100.从表4的实验结果可看出,本文算法效率较高,并且寻优结果相比文献PSO和GA较好,而且16个算例全部获得合法解.PSO算法对16个案例的寻优结果中只有10个案例找到了完全满足工期约束的调度结果,其余6个案例都存在有工件工期不能满足的情况,并且当问题规模变大,工期约束较多时,算法相对不是很理想.GA算法中有9个调度结果出现超期现象,7个合格,同PSO效果相当,交货期约束增多时算法结果均不理想.因此通过实验,本文算法在解决具有严格工期约束的无等待调度问题具有很好的优势,值得推荐. 表4 基 于 SISA-ESA算法的带有交货期约束的大规模无等待流水调度问题实验结果 针对带有交货日期约束的无等待流水调度问题,本文提出一种基于图形搜索的精确求解算法,但此算法在需调度工件≤14时能够在有限的时间内给出问题的精确解,当问题规模增加,搜索的解空间急剧增大,算法效率将不能容忍.针对此种情况,本文在原有算法基础上又提出了基于精确搜索算法的分段迭代搜索算法(SISA-ESA),并将实验结果和其他算法实验结果进行比较.结果证明本文算法性能较好,能在较短的时间内搜索到满足交货期约束的较好解.未来需要进一步研究分段大小及分段策略对算法求解结果的影响,以便对大规模问题,也能在合理时间内求出精确解.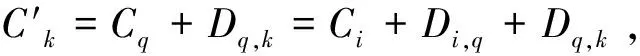
2.3 搜索算法描述
2.4 基于精确搜索的分段迭代搜索算法(SISA-ESA)
3 仿真实验及分析


4 结论

