基于数值分析的TBM动态载荷拟合*

叶尔肯·扎木提，聂晓东，贾国朋，陈立和，苗 斌，霍军周

(1.新疆额尔齐斯河流域开发工程建设管理局，乌鲁木齐 830000；2.大连理工大学 机械工程学院，大连 116024；3.中铁十八局集团有限公司，天津 300222)

0 引言

全断面掘进机(简称TBM)，是一种大型复杂的地下全断面的岩石掘进设备[1]，广泛应用于水利、交通、能源开采等地下工程建设，对其进行动力学分析、优化设计等过程时均需要有动态载荷作为输入条件，因此如何获得更为准确的TBM动态载荷显得尤为重要。由于TBM工作环境十分恶劣且自身结构的复杂性，往往造成其动态载荷的观测非常困难，因此对TBM动态载荷的获取大多采用仿真和实验的方法获得。目前国内外学者对TBM动载的拟合也进行了一些研究。汤华等[2]利用任意拉格朗日一欧拉有限元法和子模型方法，建立了模拟刀盘的掘进过程的三维数值模型，从而得到TBM相应的仿真载荷数据；屠昌锋[3]建立了仿真模型，并通过滚刀切割砂岩、盘形滚刀侵入混凝土试样和切割花岗岩的数值仿真得到了TBM相应的动态载荷；李玉钰[4]基于ADAMS仿真环境，建立了刀盘掘进过程仿真模型，并对刀盘动态掘进载荷分布情况进行了研究；夏毅敏等[5]建立了盘形滚刀破岩过程的仿真模型，并进行了相关的滚刀破岩试验，通过对理论结果、实验结果与仿真结果进行对比得到了三向动态载荷；A E Samuel等[6]对TBM现场测量了刀盘载荷，获取了滚刀载荷变化规律。现场测试环境恶劣，除了浪费大量人力物力之外，也难以精确测量每把滚刀在掘进过程中的受力情况；Zhang[7-8]、Entacher[9]等在滚刀上布置传感器，对掘进现场的某些滚刀载荷进行了测试，但未对滚刀进行种类划分处理，加之条件限制因此无法获得不同种类滚刀的载荷情况。综上所述，国内外学者虽然以对TBM动态载荷获得方法进行了大量研究，但存在如下问题：首先，目前相关研究大多以实验和仿真为主并未结合实测数据进行相应修正，存在相应的误差。其次，在进行载荷拟合时未充分考虑地质条件，滚刀类型和滚刀位置对载荷的影响，也造成了载荷拟合的误差。针对以上问题，本文首先对TBM载荷的振幅、频率、滚刀位置、滚刀类型和地质条件进行了相应的研究分析。然后，采用数值分析拟合的方法对不同地质下不同类型和不同区域的滚刀动态载荷进行了动态拟合，既兼具仿真的优点又能充分考虑到滚刀位置、滚刀种类、实际地质条件等动载影响因素。最后，结合实际情况进行误差修正，并通过蒙特卡洛方法验证了参照已有数据进行了拟合数据的验证，最终验证了本文方法的合理性和准确性。

1 分布规律研究

对于载荷分布规律研究,国外学者也做过不同的现场试验,A E Samuel[6]和Zhang[7-8]等研究表明刀具在单一岩石中掘进载荷分布是符合威布尔分布的。另外，对刀盘载荷变化曲线进行雨流统计，对雨流计数后的刀盘载荷分布进行参数估计，并用K-S方法检验并对刀盘载荷进行统计后，得到其均值、均方差,结果也表明滚刀载荷是满足威布尔分布的。

威布尔分布有多种形式，包括一参数威布尔分布、二参数威布尔分布、三参数威布尔分布或混合威布尔分布。其形状参数是最重要的参数，决定分布密度曲线的基本形状，尺度参数起放大或缩小曲线的作用，但不影响分布的形状。此处我们采用双参数威布尔分布。

如图1运用MATLAB以威布尔分布为分布规律并设置好相应的参数进行数值拟合的动载时域波形与实测数据的对比。

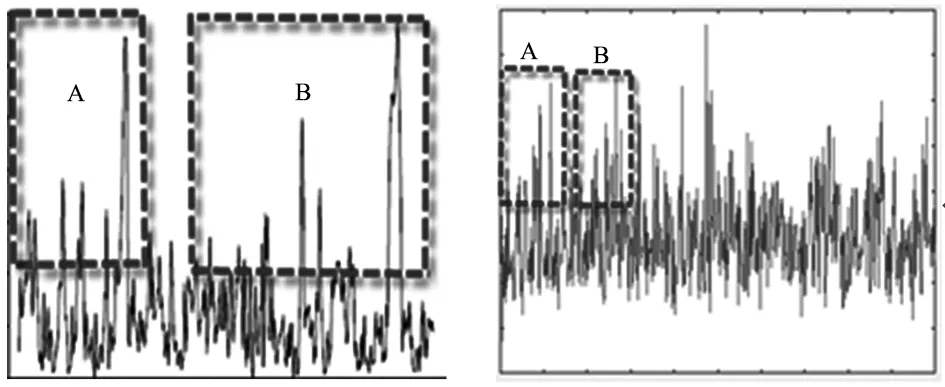
(a)实测数据波形 (b)数值拟合波形图1 分布规律对比图

对比两图中的A、B区域的波形不难看出，利用以威布尔分布为分布规律进行数值拟合的动载时域数据是较为合理的。

2 振幅研究

由于同一种力其对于不同的滚刀的动载曲线是不同的，以垂直载荷为例，对Zhang、Entacher、A E Samuel等[6-9]实测数据进行分析可见：

(1)边滚刀垂直动载基本在均值的10%～15%之间波动；

(2)正滚刀垂直动载基本在均值的20%～25%之间波动；

(a)中心滚刀仿真载荷时域波形

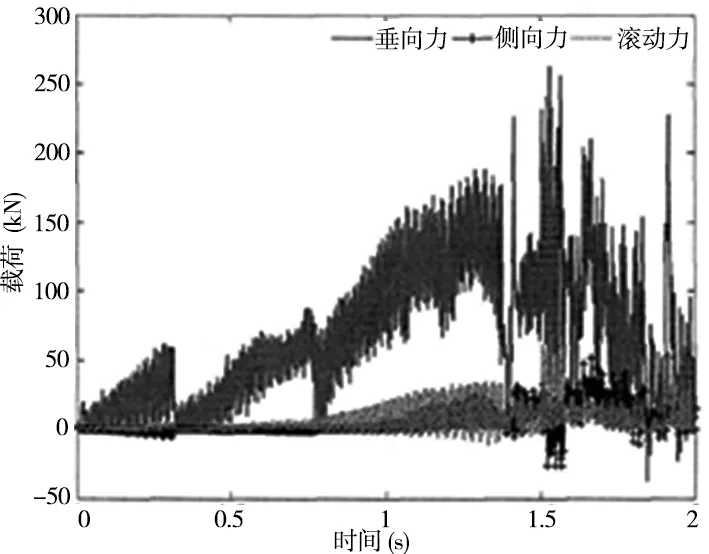
(b) 正滚刀仿真载荷时域波形

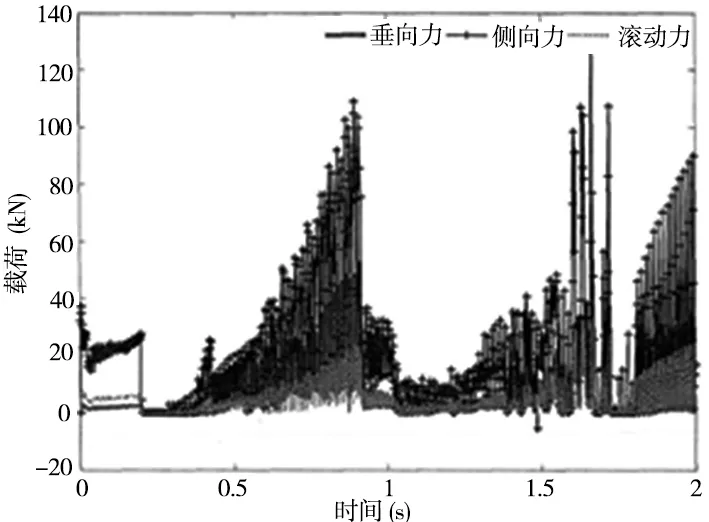
(c) 边滚刀仿真载荷时域波形图2 三种滚刀仿真载荷时域波形

表1 结果统计

由图2仿真分析结果[10]可知：滚刀的各向载荷呈现阶跃性且三向力的变化趋势基本相同;中心滚刀和正滚刀的各向载荷变化趋于基本一致,垂向力是最大的,侧向力是最小的。

对仿真数据进行统计得到表1所示的结果。

由表中统计结果可知：中心滚刀、正滚刀垂向载荷均值相差17%左右。

经过以上分析，总结可得：

(1)滚刀的各向载荷呈现阶跃性,三向力的变化趋势基本相同；

(2)中心滚刀和正滚刀的各向载荷变化趋于一致, 侧向力是最小的，垂向力最大；

(3)边滚刀垂直动载基本在均值10%～15%之间波动；

(4)正滚刀垂直动载基本在均值20%～25%之间波动；

(5)对中心滚刀，中心滚刀与正滚刀垂向载荷均值相差17%左右,因此中心滚刀的动载数据近似的在正滚刀的基础上乘83%即可。

3 频率研究

本课题组由LS-Dyna得到不同滚刀载荷时间历程曲线如图3所示。

(a)中心滚刀三向载荷

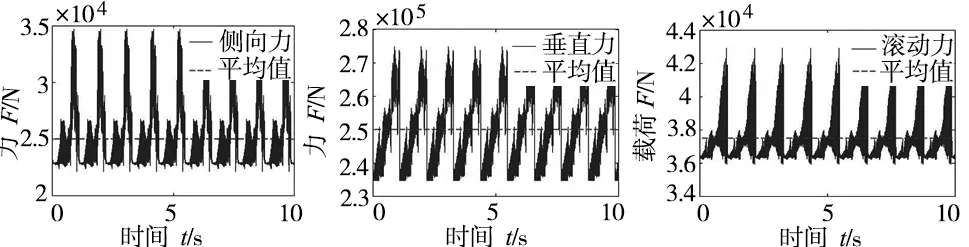
(b)正滚刀三向载荷

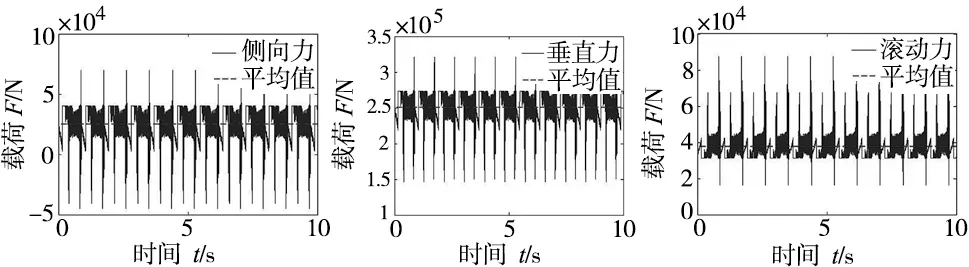
(c)边滚刀三向载荷图3 三种滚刀三向载荷仿真时域波形图

对图3展示的三向载荷的时域波形使用傅立叶函数变换得到频谱图如图4所示。

(a)中心滚刀 (b) 正滚刀 (c) 边滚刀图4 三向载荷频谱图

从滚刀载荷频谱图4中可以看出，滚刀载荷绝大多数基本集中在0～7Hz之间，具有低频的特性。对图4频谱图的中心滚刀、正滚刀、边滚刀三向载荷的频率进行统计如表2所示。

表2 滚刀频率统计表

从对滚刀频率的统计可知，中心滚刀载荷频率大多集中在0～5Hz；正滚刀载荷频率大部分集中在0～5Hz；在频率125 Hz集中了少量载荷；边滚刀载荷频率集中在0～5Hz外，仍有少部分载荷集中在120Hz、208Hz、300Hz；因此可以看出刀盘滚刀在掘进时载荷绝大多数集中在0～5Hz，具有典型的低频特性，这里我们为了让载荷的涵盖性更广，我们取最大频率5Hz进行拟合。

4 滚刀种类与位置与地质条件研究

考虑滚刀位置即考虑不同位置的滚刀受到的载荷大小和波动是不同的，如图5所示，1～8为中心滚刀基本处于内圈力的波动差不多，中心滚刀用一套载荷时域波形图，边滚刀均处外圈故也用一套载荷时域波形图，但正滚刀数量较多，占据大半个盘面如图所示，因此将正滚刀分为内中外三层不同的载荷，采用三种不同的载荷时域。

图5 刀盘滚刀分布图

另外由于中部滚刀在刀盘中部刀面上，以中部代表垂直载荷，外部正滚刀和内部正滚刀以中部正滚刀垂直载荷乘以波动比值做参数来间接得到。

在地质因素方面，由静载分析的结果可得，软岩的载荷以硬岩的载荷的1/3来赋值，所以动载对其进行沿用，软岩的动载载荷时域波形图以硬岩动载载荷时域波形图的1/3进行拟合，这样既能保证与静态载荷软硬岩石转化相一致又能保证可行性和合理性。

5 误差处理及载荷验证

5.1 误差处理

由于经过以上分析和修正时域载荷波形，波形图下部仍然会存在一定的超差数据如图6所示，提取500个采样点进行分析。

图6 修正前波形图

对于超差数据应对措施为：将点去除后拟合一种符合标准小区域的威布尔分布图(由于超差区域出现在下部分，又由于下面的数据波动较小，所以用均值的5%进行界定)，采样得到N组数据，然后从1～N个整数里随机选取一个整数作为序号，以此序号从数组中选择相应的数据进行填充，这样既能保证载荷的随机性，又能达到随机的目的，修正后的的波形如图7所示。

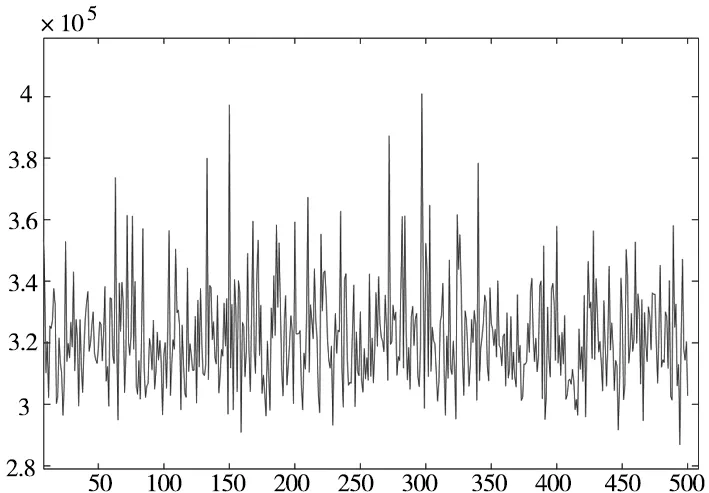
图7 修正后波形图

可以看出，用以上方法处理数据基本控制在合适的范围内了，达到了控制误差的效果。

5.2 载荷验证

拟合出的载荷时域波形图采样点绘出如图8所示载荷波形：

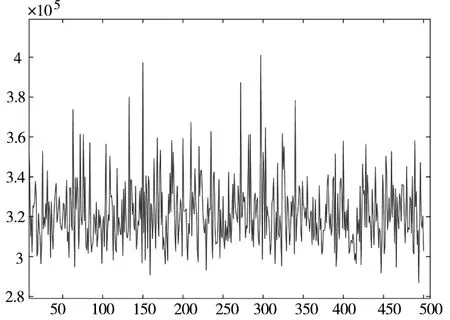
图8 采样得到波形图

可以看出，拟合的该载荷时域波形图呈现阶跃性与实际情况相符合；其载荷波动基本稳定在均值的20%左右与实测数据吻合。

由以上可验证了拟合的时域波形满足了分布形式和波动区间，为了进一步验证拟合的时域波形各个区间的数值也基本吻合，因此由蒙特卡洛方法在相同条件下取了5000个采样点比较了已有数据与数值拟合的数据在不同区间力的占比如表3和表4所示。

表3 Ls-Dyna数据占比

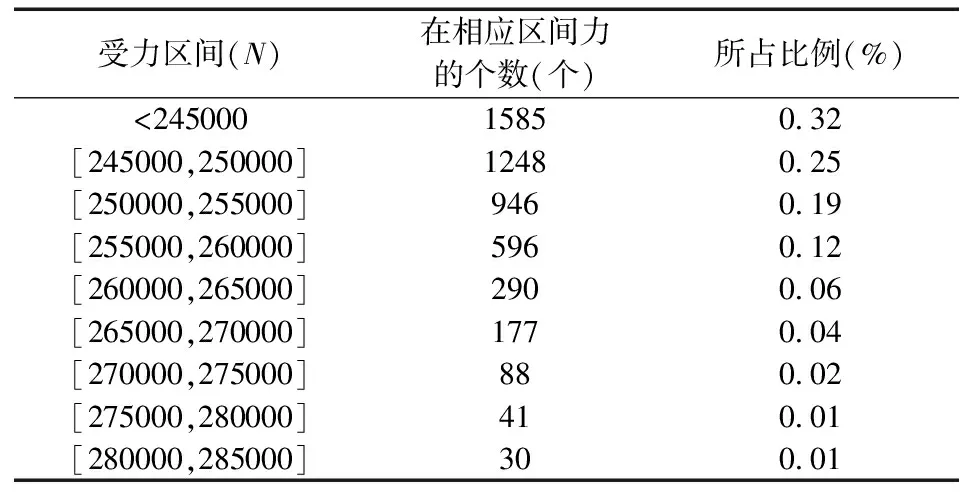
表4 拟合数据占比

图9 两种数据对比图像

由图9可见：通过对采样数据进行统计分析，已有数据与拟合载荷的占比最大差值只有4%，其可信度达到了96%，在概率中是满足置信度要求的，所拟合的载荷是符合要求的。

6 结论

本文采用数值分析拟合法并结合了雨流记数法等方法，首先对实测和仿真结果进行分析，得到动载的分布规律、振幅和频率与载荷的关系，并用MATLAB进行拟合得到初步动态载荷并根据实际情况加上滚刀位置、滚刀种类、地质条件对原有载荷进行修正；然后与仿真结果进行对比，进行误差修正，最终可得到中心滚刀的三向载荷、正滚刀中部外部内部三向载荷、边滚刀三向载荷，最后运用蒙特卡洛方法验证了拟合的数据与已有数据基本在置信区间内，验证了方法的可行性。此方法克服了纯粹仿真中的诸多问题，更接近实际情况。