基于优化采样支持向量机的指纹二值化方法
李俊杰,高翠芳,黄 芳
(江南大学理学院,江苏 无锡 214122)
0 引言
指纹作为一类常用的生物识别特征[1],与面孔、发音、虹膜、骨形等其他生物识别特征一样,具有唯一性、稳定性等特点.相比于面孔、发音等易采集的生物识别特征,指纹具有一定的私密性,同时相比于虹膜、骨形等较复杂的生物识别特征,指纹又便于采集.综合上述特点,指纹识别技术被广泛应用在基于身份验证的支付、安防等相关邻域.[2-3]近年来,随着智能移动终端的快速发展,指纹识别技术已被大量应用到智能移动终端上[4],被快速商业化应用.
在指纹识别过程中,一个关键步骤就是将从传感器上采集来的指纹图像进行二值化处理[5].经二值化后的指纹图像仅留下前景指纹和背景部分,去除了原图中的灰度噪声,极大方便了后续的识别配对.现有的指纹二值化处理大多采用基于指纹纹理的方向场技术[6-7],少部分基于滤波算法来实现[8].采用方向向量将含有灰度信息的指纹图像转化为二值图像,基于方向技术的指纹图像二值化算法可以同时完成指纹图像的二值化处理以及细化处理.但方向场技术在计算过程中需要计算每个像素的方向向量,算法复杂度高,计算时间长,在实际应用中存在一定的局限性.
考虑现有指纹二值化处理中存在的问题,本文提出基于支持向量机(SVM)的指纹二值化处理方法.SVM[9]是一种有监督的小样本分类方法,可利用先验知识,通过小样本快速完成分类.指纹二值化处理中,前景和背景在分类前具有一定的先验知识,灰度值较小的通常是前景,灰度值较大的通常是背景,凭此可运用SVM进行指纹二值化处理.
在SVM分类过程中,如果只采用像素值一个特征量,可能会降低分类精确度,尤其是在指纹图像边缘处.因此,本文又提出了一种4-邻域均值模板来处理指纹图像边缘,并以此作为另一个特征量.同时利用灰度直方图搜索算法,提取统计值较高的像素点作为训练集,通过4-邻域均值模板以及直方图搜索优化训练集来提高分类精度.
1 支持向量机简介
对于数据集T={[x1,y1],[x2,y2],…,[xN,yN]},{x1,x2,…,xN}∈RN为数据集的输入空间,同时每一维x都有N个特征组成;{y1,y2,…,yN}∈{-1,1}为数据集中每一维输入空间对应的类属标签.SVM的目的是利用输入空间以及标签集对数据集T进行分类.

SVM作为一种有监督式的学习算法,在一定程度上依赖于标签集的分类,因此在处理不确定标签问题时存在一定的局限性,例如指纹灰度图像中指纹图形的边缘像素点既可看作前景类,也可看作背景类.不同的标签类会影响分类结果,对训练造成影响.针对这一问题,本文在原有指纹图像像素值的基础上引入新特征量来扩充SVM中的训练集.同时采用出现频率高的像素点作为样本点,使分类精度进一步提高.
2 优化采样算法
指纹通过传感器采集得到灰度图像,灰度图像用灰度值存储为矩阵形式[5],不同的灰度值代表了图像中不同的灰度,因此像素点灰度值可作为SVM学习过程中一个重要的特征.但是只有一维特征的情况下会导致分类结果出现偏差,尤其是在图形边缘的像素点,因此本文定义4-邻域均值模板来处理图形边缘,并以其计算值作为另一维特征.
在样本点的采样过程中,为提高计算速度,本文采用等距采样,同时为了提高分类精度,在等距采样的基础上加入基于灰度直方图的优化算法,将等距采样后样本点周围直方图统计量较多的像素点作为样本点,进一步提高了分类精度.
2.1 基于4-邻域均值模板辅助样点
在指纹灰度图像的前景和背景分类问题中,指纹纹理与纹理过度部分存在图像边缘的问题[10],边缘像素点判定会影响到后续的匹配识别,本文设计了4-邻域均值模板,来提高算法在边缘点分类上的精确度.
设计的4-邻域均值模板是在边缘检测算子的基础上演变而来的.参考Prewitt算子[11]设计4-邻域均值模板,Prewitt算子表达式为
(1)
在传统的Prewitt算子中分别对列Gx和行Gy进行计算,共计算中心像素点周围8个像素点的值.为方便计算,考虑将行列融合,并且只计算上下左右4个方向的像素,通过模板中心像素点灰度值与4个方向像素点灰度值的差值绝对值的平均来构造4-邻域模板:

(2)
由(2)式可知,4-邻域均值模板D计算了中间像素点Ii,j与上方像素点Ii-1,j、下方像素点Ii+1,j、左侧像素点Ii,j-1、右侧像素点Ii,j+1之间的差值的绝对值,通过相加这4个方向的差值,得到
∑D=(|Ii,j-Ii-1,j|+|Ii,j-Ii+1,j|+|Ii,j-Ii,j-1|+|Ii,j-Ii,j+1|).
(3)

4-邻域均值模板相比于边缘检测中的Prewitt算子对模板中心像素点的权值更大,更能突出模板中心点像素值的重要性,同时通过一个模板计算4个方向,不需要2个模板计算,提高了计算速度.
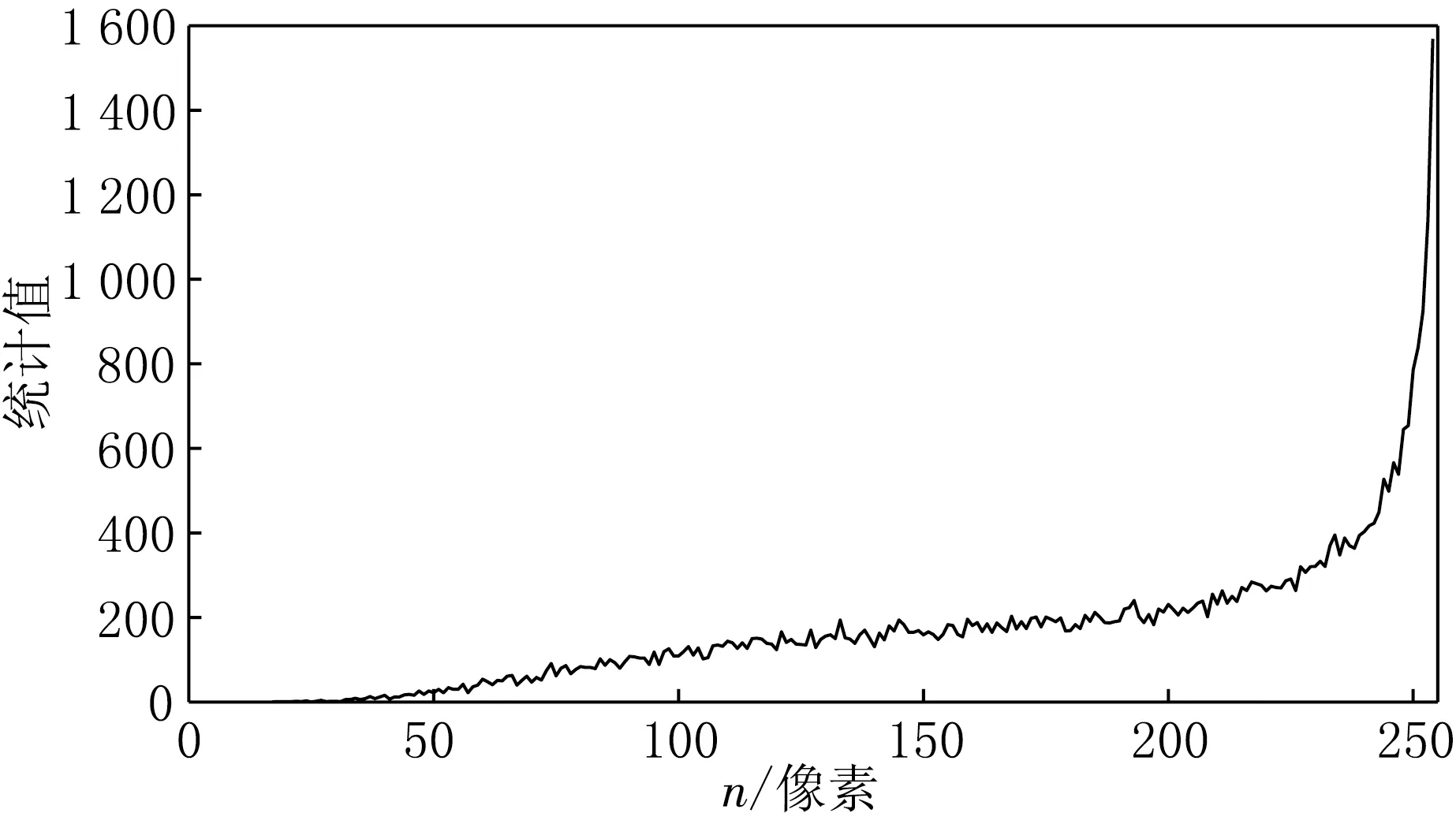
在对生物图像、医学图像等客观图像处理时,需要保证图像的原有特性[5],应避免非线性变换,本文所构造的4-邻域均值模板就可以较好地满足这一点.以指纹图像的灰度直方图为例,计算结果如图1所示.

(a)原始指纹图像

(b)4-邻域均值模板处理图像
(a)原始指纹图像灰度直方图

(b)4-邻域均值模板处理图像灰度直方图
图1中白色背景都占据了绝大部分比例,为显示图像的特点,本文手动去除了直方图中灰度值为255的点.通过比较发现,两者图像走势基本相同,因此4-邻域均值模板能较好地保存原图像特征.
在原有的特征量基础上,加入4-邻域均值模板计算结果作为特征量,能在一定程度上提高SVM在图像边缘点判断的准确性.
2.2 直方图搜索算法
在灰度图像中,灰度直方图是刻画像素灰度值统计量的一个重要工具,在SVM训练样本点的选取中,为了使分类更加精确,需要更为准确的先验知识,因此选择统计值较大的像素点作为SVM的训练样本.但是为提高计算效率,保证样本多样性,本文采用局部统计值最大的像素点作为训练样本点,寻找样本点的方法就是本文的直方图搜索算法.
直方图搜索算法分为2个部分,第一部分是对整个样本空间进行等距采样,即采用相等的间距对255个灰度值进行采样,等距采样公式为

Ii=Num255n-1∗i(i=2,3,…,n-1).
(4)
其中:I为样本点,且I1=0,In=255;n为采样个数;Num255为将二维图像矩阵展开成一维向量,并从0到255进行排序后,255像素第一次出现所对应的值,本文对Num255之前的像素进行等距采样,并进行直方图搜索;i为样本点标号,由于样本点首尾固定,所以i从2标到n-1;符号└┘为向下取整,保证样本点标号为整数.
基于等距采样的样本点无法保证每个样本点都有较大像素统计量,因此第二部分是在等距采样的基础上进一步提出了直方图搜索算法,在当前样本点的基础上搜索它的前一个像素值以及后一个像素值,用最大的那个作为样本点,以此来保证样本点在局部范围内有一个较大的像素统计量.算法1的直方图搜索算法伪代码为:

01 Begin02 输入I_i //获取当前采样点03 输入H_i //获取当前像素值04 输入I_i-1 //获取前一个采样点05 输入H_i-1 //获取前一个像素值06 if H_i>H_i-1 then07 H_i≥H_new08 I_i≥I_new09 else10 H_i-1≥H_new11 I_i-1≥I_new12 输入I_i+1 //获取后一个采样点13 输入H_i+1 //获取后一个像素值14 if H_i+1 算法1中I_i存储了所选取的样本点,H_i存储了样本点对应的像素统计值,本文对等距采样的结果进行直方图搜索更新.通过算法1可以实现样本点的像素统计值在局部范围内达到一个极大值,由此来提高SVM的优化精度.直方图搜索算法的结果如图3所示. 图3 直方图搜索算法的结果 在图3中黑色圆点表示等距采样的结果图,黑色圆圈表示在等距采样的基础上经过直方图搜索算法优化的结果,从图3中可以看出,经过优化后样本点的像素统计值均到达局部极值点. 在实际测试中,本文采用FVC2004数据库中的指纹图像作为实验数据[12].该数据库中包含有4种类型传感器收集来的数据.对于产生如图1(a)的指纹传感器,从图1中可以看出图像构成只包含前景和背景两类,且指纹图像不存在复杂区域,构成简单,因此对二值化算法的要求较低,各算法二值化结果相近. 本文考虑处理较为复杂的一类传感器所得图像.此类传感器收集的指纹图像大小为328像素×364像素.由于传感器因素,图像形成了一个类似透视效果的形变,因此在图像中产生了2个背景,一个为白色背景,一个为深灰色背景.同时由于传感器原因,使得指纹图像中间产生了一个深色复杂区域.具体指纹图像见图4(a). 在本文算法实际处理时,采用SVM进行二值化处理.SVM训练集选取直方图搜索算法,所得样本点的灰度值以及对应4-邻域均值模板的计算值为特征量,直方图搜索算法选择30个像素样本点.以此训练结果对全部像素点进行前景和背景分类.同时将本文算法与未经过优化采样的原始SVM算法及模糊聚类算法进行了对比. 对于经过透视变换导致形变的指纹图像,本文算法二值化结果、原始SVM的二值化结果如图4所示. (a)形变后指纹图像 (b)本文算法结果 (c)原始支持向量机结果 本文算法二值化结果与原始SVM二值化结果的数值统计见表1. 表1 形变后指纹图像二值化处理对比数据 两种算法对深灰色背景、白色背景都进行了有效地处理,在背景上只留下少许噪声点.从统计数值中可以看出,本文算法在背景上的残留噪声点在背景像素点中的占比为4.53×10-4,原始SVM占比为5.05×10-4.对比背景残留噪声点,本文算法对误判降低了10.21%.但由于两种算法所得图像的背景残留噪声点的占比都较小,均不影响后续处理. 对于指纹中间的被污染的深色复杂区域,从直观结果中可看出,本文算法的二值化结果要优于原始SVM二值化结果.本文选择100像素×3 100像素的区域对原始指纹图像中的深色复杂区域进行放大,两者的细节对比如图5所示. (a)形变后指纹对比区域 (b)本文算法结果 (c)原始SVM结果 通过统计结果可知,本文算法二值化后误判的像素在放大区域中的占比为0.005 3,原始SVM占比为0.009 5,本文算法有效降低了45.92%的误判.同时从直观结果中可见,原始SVM二值化处结果中存在明显的黑色块,且遮挡了一个指纹的分叉点,而本文算法也存在误判,但占用像素少,没有形成明显的黑色块,没有遮挡指纹中的重要结构. 通过上述对比可以看出,本文算法在处理指纹图像的边缘细节以及复杂区域较为准确,所提出的4-邻域均值模板和直方图搜索算法可有效提高SVM在指纹二值化处理中的分类精度. 将本文算法与模糊聚类算法(FCM)[13]相比较.FCM是一种无监督的分类算法,被广泛运用于各个邻域.在相同计算环境下,采用本文算法和FCM对形变后指纹图像进行二值化处理,结果如图6所示. (a)形变后指纹对比区域 (b)本文算法结果 (c)FCM算法结果 从图6可见,本文算法结果远好于FCM,尤其是在图6(c)中,结果图像中存在几处的黑色块,且背景上的黑色块也较多,会大大影响后续识别的效果.两种结果的数据对比见表2. 表2 本文算法与FCM实验结果对比 通过表2数据看出,在相同的计算环境下,本文算法的计算处理速度远快于FCM.同时由统计可知,对于背景的处理FCM二值化后背景残留噪声点在背景像素点中的占比为5.772×10-3,而本文算法为4.53×10-4.相比FCM本文算法降低了92.15%的误判. 对于复杂区域,从直观可见,FCM算法将复杂区域二值化为整个黑色块,几乎失去了全部细节,而本文算法则保留了较好的细节部分.本文算法在不丢失主要细节的前提下,图像占比更小,将更有利于后续的识别算法. 基于本文提出的优化采样算法,利用SVM对指纹图像进行二值化处理的方法可有效地解决SVM在指纹图像边缘以及复杂区域分类精度低的问题,能较好地保存指纹细节,配合其他模式识别算法,可有效地完成指纹识别工作. 本文在SVM的基础上,加入了基于4-邻域均值模板和直方图搜索算法的优化采样方法,进一步提高了识别精度,对算法做出了有益的改进.本文算法相比于同为分类算法FCM算法,计算精度较高,计算量较小,实验结果也说明了本文算法是有效可行的.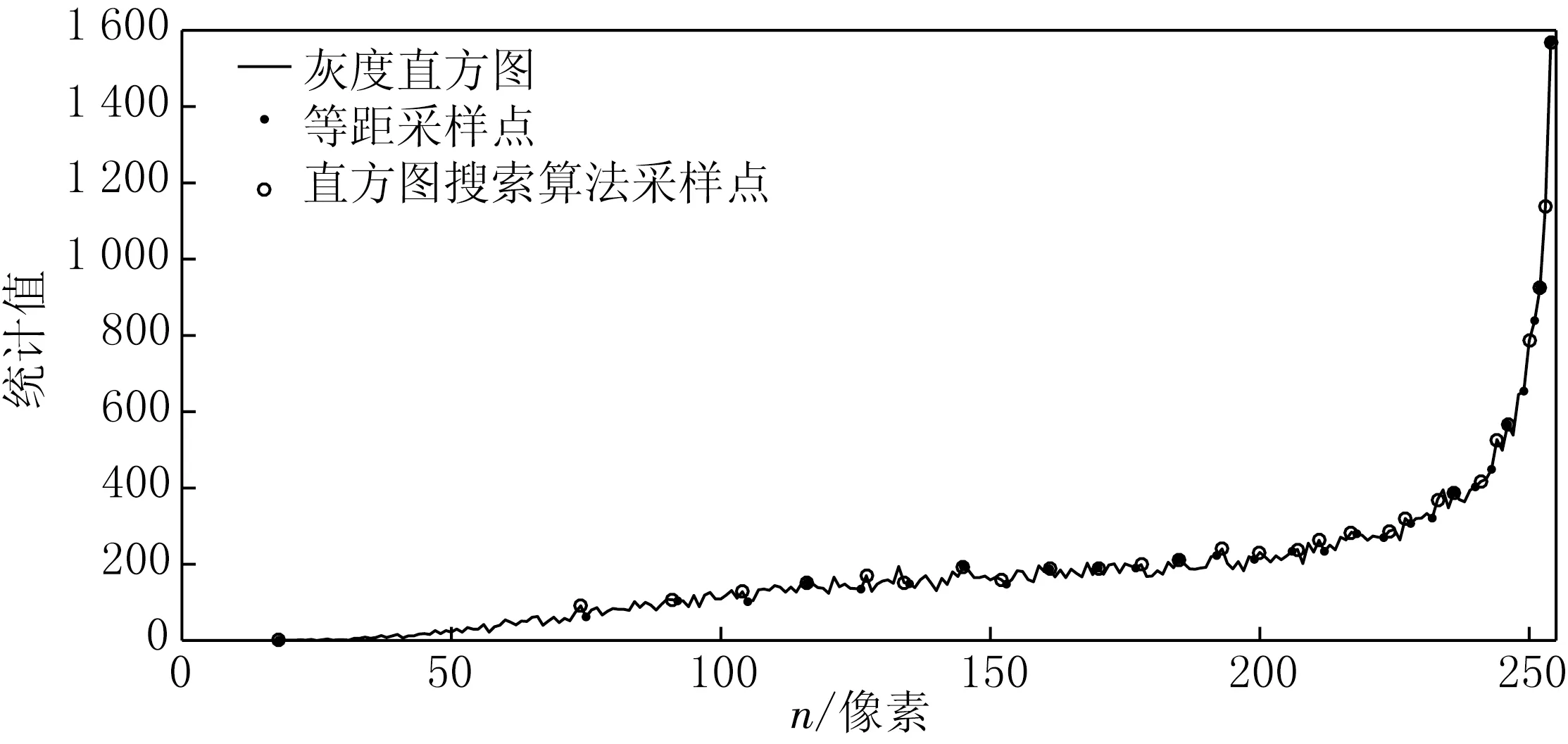
3 指纹图像二值化处理与比较结果
3.1 对比原始SVM算法结果







3.2 对比模糊聚类算法结果




4 结论

