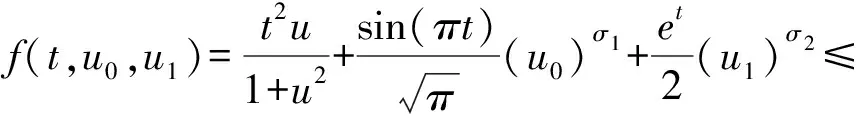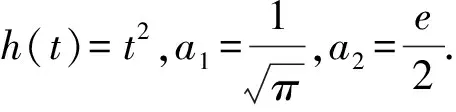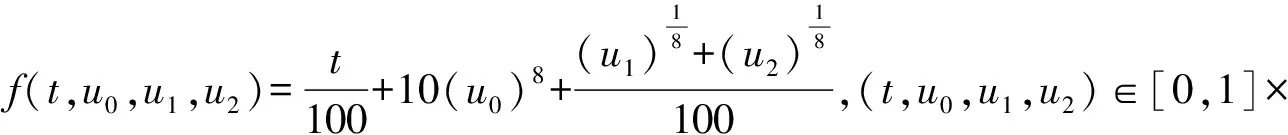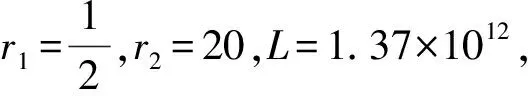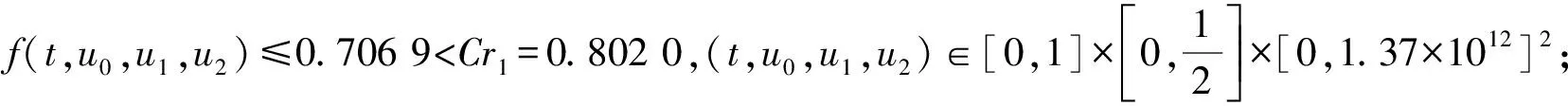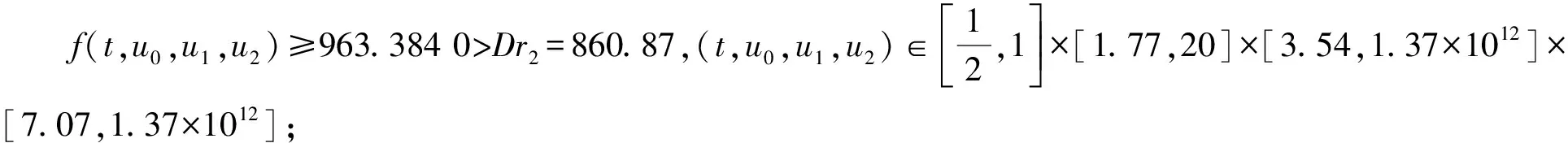一类分数阶微分方程边值问题正解的存在性
冯 立 杰
(天津大学数学学院,天津 300350)
0 引言
近年来,分数阶微分方程受到了广泛关注.与整数阶微分方程相比,分数阶微分方程应用范围更广,其在物理学、生物学、分析化学等领域发挥了重要的作用.[1-2]许多学者对分数阶微分方程进行了深入的研究,取得了丰硕的成果.[3-7]
文献[7]运用单调迭代法,研究了分数阶微分方程边值问题
本文考虑非线性分数阶微分方程边值问题
(1)
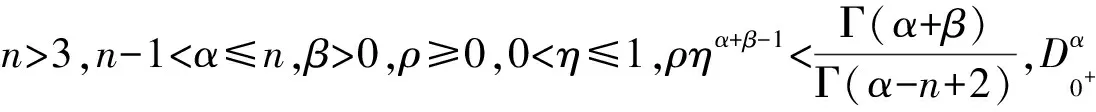
1 预备知识
定义1[1]函数y:(0,+∞)→R的阶数为α>0的Riemann-Liouville分数阶积分定义为
这里等式右边是在(0,+∞)上逐点定义的.
定义2[1]函数y:(0,+∞)→R的阶数为α>0的Riemann-Liouville分数阶导数定义为
其中:n=[α]+1,[α]表示α的整数部分;右边在(0,+∞)上是逐点定义的.
引理1[1]假设y∈C(0,1)∩L1(0,1)且α>0,则
其中ci∈R,i=1,2,…,n,n如定义2所述.
引理2[1]假设y∈L1([0,1],R),且p>q>0,则对任意的t∈[0,1],有:
引理3给定y∈C[0,1],n-1<α≤n,β>0,则分数阶微分方程
(2)
(3)
的唯一解为
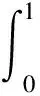
其中
(4)
这里d=[Γ(α+β)-Γ(α-n+2)ρηα+β-1]-1>0.
证明根据引理1可知方程(2)的一般解为
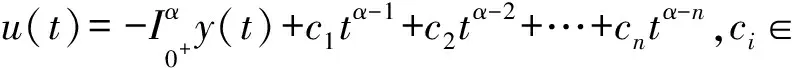
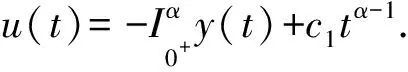
因此
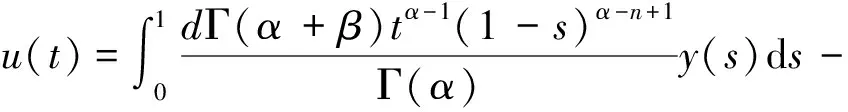
(5)
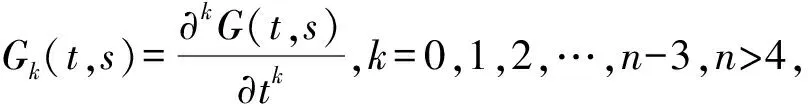
(6)
引理4函数Gk(t,s)有以下性质:
(ⅰ)Gk(t,s)是连续函数,并且满足Gk(t,s)≥0,t,s∈[0,1],k=0,1,2,…,n-3;
(ⅱ) 对任意的t,s∈[0,1],有tα-k-1Gk(1,s)≤Gk(t,s)≤Gk(1,s),k=0,1,2,…,n-3.
证明(ⅰ) 由等式(6)可知Gk(t,s)为连续的.
当0≤s≤min{t,η}≤1时,
当0≤t≤s≤η≤1时,
当0<η≤s≤t≤1时,
当0 (7) 另外,显然有Gk(t,s)≥tα-k-1Gk(1,s).结论证毕. 引理5[8](Schauder不动点定理) 设U是Banach空间E中的一个非空有界闭凸子集,T:U→U是全连续算子,则T在U中至少存在一个不动点. 设E是一个Banach空间,P⊂E是一个锥.假设α,β:E→R+是两个连续的凸泛函,并且满足:对于u∈E,λ∈R有α(λu)=|λ|α(u),β(λu)=|λ|β(u);当u∈E时,‖u‖≤kmax{α(u),β(u)};当u1,u2∈P,u1≤u2时,α(u1)≤α(u2),其中k是一个常数. 引理6[9]令r2>r1>0,L>0都是常数, Ωi={u∈E|α(u) 是E上的两个有界开集.记Di={u∈E|α(u)=ri}.假设T:P→P是全连续算子并且满足: (ⅰ)α(Tu) (ⅱ)β(Tu) 定义E=Cn-3[0,1],定义范数 则(E,‖·‖)是一个Banach空间. 定义如下形式的锥: P={u∈E|u(k)(t)≥0,u(k)(t)≥tα-k-1‖u(k)‖0,t∈[0,1],k=0,1,2,…,n-3; u(i)(0)=0,i=0,1,2,…,n-4}. 在P上定义算子T为 (8) 则算子T的不动点即为边值问题(1)的解. 证明首先证明算子T:P→P.根据引理4,有(Tu)(k)(t)≥0,∀t∈[0,1],k=0,1,2,…,n-3.另外, 且 因此算子T:P→P. 下面证明算子T是全连续的.由于函数G,f都是连续的,所以算子T是连续的.设Ω为E中的任意有界集,则存在常数N>0,对∀u∈Ω,有‖u‖≤N.记 对∀u∈Ω,由引理4可知 所以,T(Ω)为一致有界的. 另一方面,∀t1,t2∈[0,1],不妨设t1 当t1→t2时,上述不等式趋于0.因此T(Ω)为等度连续的. 则边值问题(1)至少存在一个正解. 证明定义有界集Br={u∈P|‖u‖≤r},其中: 下证T:Br→Br.如果u∈Br,有 因此 又根据引理7知T:Br→Br是全连续的,从而由Schauder不动点定理可得边值问题(1)至少存在一个正解. 定义泛函 则有: α(λu)=|λ|α(u),β(λu)=|λ|β(u),λ∈R; 当u1,u2∈P,u1≤u2时,α(u1)≤α(u2). 记 其中0<γ<1. 定理2假设L>r2>γα-1r2>r1>0,其中0<γ<1为常数.f(t,u0,u1,…,un-3)满足以下条件: (H1)f(t,u0,u1,…,un-3) (H2)f(t,u0,u1,…,un-3)≥Dr2,(t,u0,…,uk,…,un-3)∈[γ,1]×[γα-1r2,r2]×…×[γα-k-1r2,L]×…×[γα-n+2r2,L]; (H3)f(t,u0,u1,…,un-3) 则边值问题(1)至少有一个正解u(t)满足 r1<α(u) 证明对f做如下修改: 依次进行下去有 考虑边值问题 (9) 定义 Ω1={u∈E|α(u) 与 Ω2={u∈E|α(u) 为E中的两个有界开集.记 D1={u∈E|α(u)=r1}, D2={u∈E|α(u)=r2}. 分三步对定理进行证明. 步骤一:对u∈D1∩P有α(u)=r1,0≤u(t)≤r1. 由(H1), 对u∈D2∩P,有α(u)=r2,‖u‖0=r2,0≤u(t)≤r2,t∈[0,1].另u(i)(0)=0,i=0,1,2,…,n-4. 由 可得 ‖u(i)‖0≤‖u(i+1)‖0,‖u(k)‖0≥‖u‖0=r2,k=1,2,…,n-3. 因此 u(k)(t)≥γα-k-1‖u(k)‖0≥γα-k-1r2,t∈[γ,1],k=0,1,2,…,n-3. 其中0<γ<1.由(H2), 步骤二:根据(H3),对于u∈P有 步骤三:由α(u)的定义,存在一个非负函数p∈{(Ω2∩P)�}使得α(p)≠0,并且对所有的u∈P和λ≥0有α(u+λp)≥α(u).例如,令 r1<α(u) 即 从而 0≤u(t) fn-3(t,u(t),u′(t),…,u(n-3)(t))=f(t,u(t),u′(t),…,u(n-3)(t)). 则u也为边值问题(1)的解. 例1考虑边值问题 (10) 例2考虑边值问题 (11) C=1.604 0,D=43.043 5,E=0.187 9. 从而: (ⅲ)f(t,u0,u1,u2)≤2.56×1011 则由定理2可知边值问题(11)至少存在一个正解u(t)满足: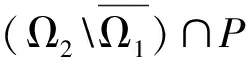
2 主要结果
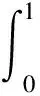
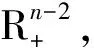
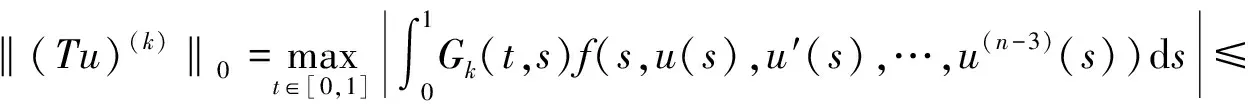
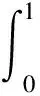
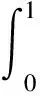
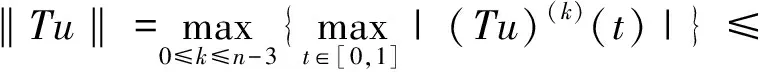
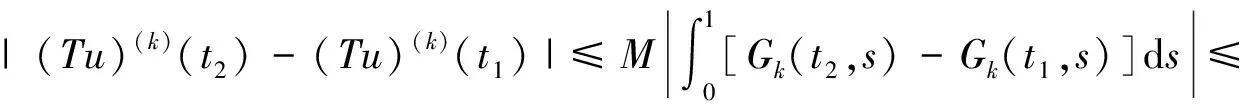
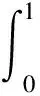
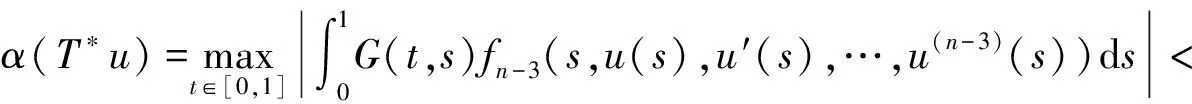
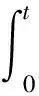
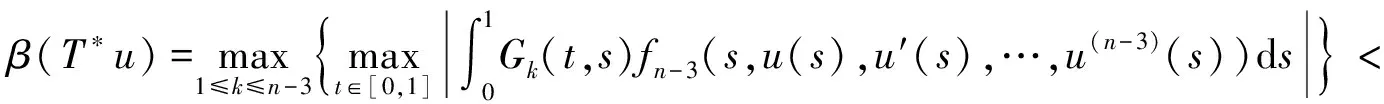
3 举例