量子气体在光晶格中的一维玻色-哈伯德模型模拟
栾 添,张雪松,陈徐宗
(1.中国电子科学研究院,北京 100041; 2.北京大学 信息科学技术学院,北京 100871)
0 概述
近年来,量子模拟引起国内外学者的广泛关注。文献[1]提出应用量子系统模拟物理问题与现象,通过可控的量子系统模拟仿真不可控的或不易解析的量子系统,获取被模拟量子系统的相关规律和信息[2]。文献[3]指出实现量子模拟的主要技术手段有光晶格囚禁超冷原子、离子阱技术、原子核自旋操控、超导电路芯片、相干光子操控等。文献[4-5]阐述了量子计算的研究方向,包括凝聚态物理、拓扑物理、高能物理、宇宙学、量子化学、分子动力学等。
目前,超冷原子量子模拟技术逐渐成为量子研究领域的热门方向[6-7]。超冷原子作为量子模拟载体[8-9]的优越性主要表现在:超冷原子在量子模拟的过程中可以保持较好的关联特性;应用Feshbach共振技术可连续调节超冷原子之间的相互作用;在超冷原子的基础上引入人造规范势模拟自旋系统。文献[10]在BEC实验上应用环形势阱实现对声波黑洞的模拟。文献[11]在超冷133Cs原子系统中引入淬火效应模拟宇宙大爆炸模型早期的非平衡演化过程,成功观测到Sakharov振荡现象。文献[12]应用超冷原子模拟激光黑洞,并观察到霍金辐射现象。文献[13]提出通用对射激光形成光学晶格囚禁超冷原子模拟凝聚态理论经典模型的构想。文献[14]利用三维光晶格囚禁超冷87Rb原子进行超流-莫特绝缘态量子相变实验,实现对三维玻色-哈伯德模型的量子模拟,以光晶格囚禁超冷原子模拟凝聚态物理中的理论模型。由于激光有“零缺陷”性,原子可以较好地囚禁在独立分布的光学格点中。另外,对光晶格的强度、频率、相位等关键参数加以调节,可以模拟一些不易实现的晶体结构类型,如一维链状结构、蜂巢结构、三角形结构、石墨烯结构等。目前,物理学家实现了对玻色-哈伯德模型(Bose-Hubbard Model)、费米-哈伯德模型(Fermi-Hubbard Model)[15]、伊辛模型(Ising Model)[16]、海森堡模型(Heisenberg Model)[17]、豪尔丹模型(Haldane Model)[18]、量子无序态模型的量子模拟[19]。
本文研究一维玻色-哈伯德模型理论及量子相变过程,应用光晶格中的超冷原子模拟一维玻色-哈伯德模型,通过观察超冷原子超流-莫特绝缘态相变过程测得相变发生的临界点,并对量子气体扩散过程中的动态空间干涉图样进行分析和比较。
1 一维玻色-哈伯德模型
玻色-哈伯德模型可以解释超导现象发生时导体中的电子在构成晶格的原子之间的运动状态。利用光晶格中的一维玻色气体对一维玻色-哈伯德模型进行模拟,当一维气体在周期性外势场Vext(x)=V0cos(kx)中时,系统的哈密顿量可以表示为[20]:

(1)
其中,m为原子的质量,k为光晶格的波矢。以格点的基态瓦尼尔函数w0(x-ia)为基对式(1)进行二次量子化(a=2π/k为晶格常数),定义算符的矩阵元:
(2)

(3)
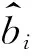
(4)
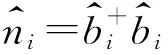
2 一维玻色-哈伯德模型量子相变
在一维玻色-哈伯德模型中,当t和U连续变化时,量子系统经历超流态到绝缘态变化的过程,是一种量子相变,称之为超流-莫特(Mott)绝缘态相变[21]。从理论上对相变进行简要分析,当t/U→0时,式(4)可以简化为[22]:
(5)
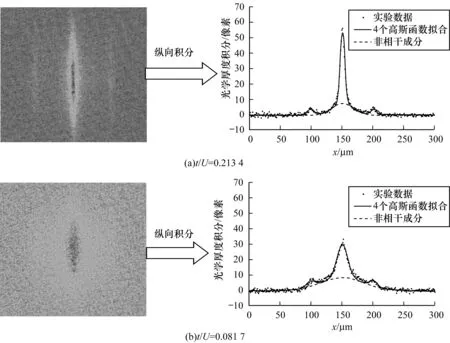
n-1<μ/U (6) 在该取值条件下,单格点的囚禁原子数仅为n时系统能量最小。定义ΔEP表示此时格点内每增加一个粒子带来的能量变化,ΔEH表示减少一个粒子带来的能量变化。则: (7) 由μ/U的取值条件可知,单格点的原子数为n时,ΔEP与ΔEH均为正值。无论格点内增加或减少一个原子都将使格点的整体能量增加,只有通过外界能量参与才能强制改变这种状态,即可以看成是格点内单原子激发存在着能带间隔。从式(4)可以看出,隧穿项(-t)带来的能量变化使系统的能量减少,当t 图1 一维玻色-哈伯德模型超流-莫特绝缘态相变 光晶格的周期性势阱是研究一维玻色-哈伯德模型的理想手段,一般先以超冷原子为基础制备一维玻色气体,然后在一维玻色气体上加载一维光晶格,通过调节光晶格的势阱深度改变原子在格点之间的隧穿项,实现超流-莫特绝缘态的量子相变。 采用87Rb超冷原子实验系统来进行量子模拟实验,在制备完成87Rb玻色-爱因斯坦凝聚体(Bose-Einstein Condensate,BEC)后,得到原子数为1.6×105,纯度约为90%,处于|F=1,mF=-1〉超精细能态上的BEC。以e指数的形式绝热加载势阱深度为50Er的1 064 nm二维光晶格激光(Er为原子的反冲能量)。在加载光晶格的过程中,采用磁悬浮的方法平衡87Rb原子的重力。由于原子在横向上的束缚比较强(横向束缚频率ω⊥=2π×30 kHz),满足一维气体条件:μ,kBT<<ωr,因此,原子在空间中看作是处在整齐排列的一维管道中,每个管道中的原子可以近似成一维玻色气体(一维束缚频率ωx=2π×83.3 Hz,相互作用参量γ=0.57),如图2(a)所示。 图2 量子模拟实验 在一维方向上以相同的时序加载852 nm对射激光形成光晶格,形成周期性势场,光晶格的势阱深度由1Er连续调节至50Er,以连续改变原子在相邻格点之间的隧穿强度。在实验中,t/U可以从0.002 6连续变化到1.106,采用时间飞行(Time of Flight,TOF)方法来进行成像,图2(b)为实测到的一维玻色气体超流-莫特绝缘态动量空间相变图。从图2(b)可以看出,随着光晶格势阱深度的增加,一维玻色气体的动量空间发生连续的变化。 为研究光晶格中超冷原子在相变过程的特性,采用双高斯拟合的方法对原子在动量空间的物质波干涉图样进行分析,以分辨出超流成分和莫特绝缘态成分在相变过程中的变化。在实验时序上,制备一维气体时加载一维方向上852 nm的光晶格。在晶格加载完毕后,原子在光晶格中静置30 ms,并在50 μs内迅速将光晶格势阱深度增加至30Er(t/U=0.012 6),将所有的激光和磁场关断并做30 ms的TOF成像。该过程可以看作是将原子的波函数向30Er阱深下的光晶格能带做一个投影,完整保留一维气体方向的相干信息。 (8) (9) 图3 光晶格中一维玻色气体动量空间干涉图样及纵向积分 图3(b)是在t/U=0.081 7(13Er)条件下得到的干涉图样,相干峰成分较图3(a)有所降低,非相干成分增加。 图4 光晶格中一维玻色气体随平均原子数密度和t/U变化的超流成分映射 本文以凝聚态物理中的一维玻色-哈伯德模型为基础,从理论角度研究了超流-莫特绝缘态的量子相变过程,在超冷87Rb原子实验系统上制备一维玻色气体,在此基础上加载852 nm光晶格囚禁超冷原子,对一维玻色-哈伯德模型进行量子模拟。同时,研究了在超流-莫特绝缘态相变过程中一维玻色气体动量空间的变化情况,利用连续改变光晶格中一维玻色气体的密度和光晶格势阱深度得到超流成分映射图。实验结果表明,光晶格中的量子气体可以较好地对一维玻色-哈伯德理论模型进行模拟。下一步将改进、完善实验系统,在大参数范围内调节原子的密度,以便模拟凝聚态物理学中的理论模型。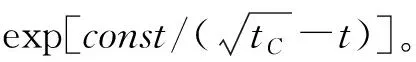
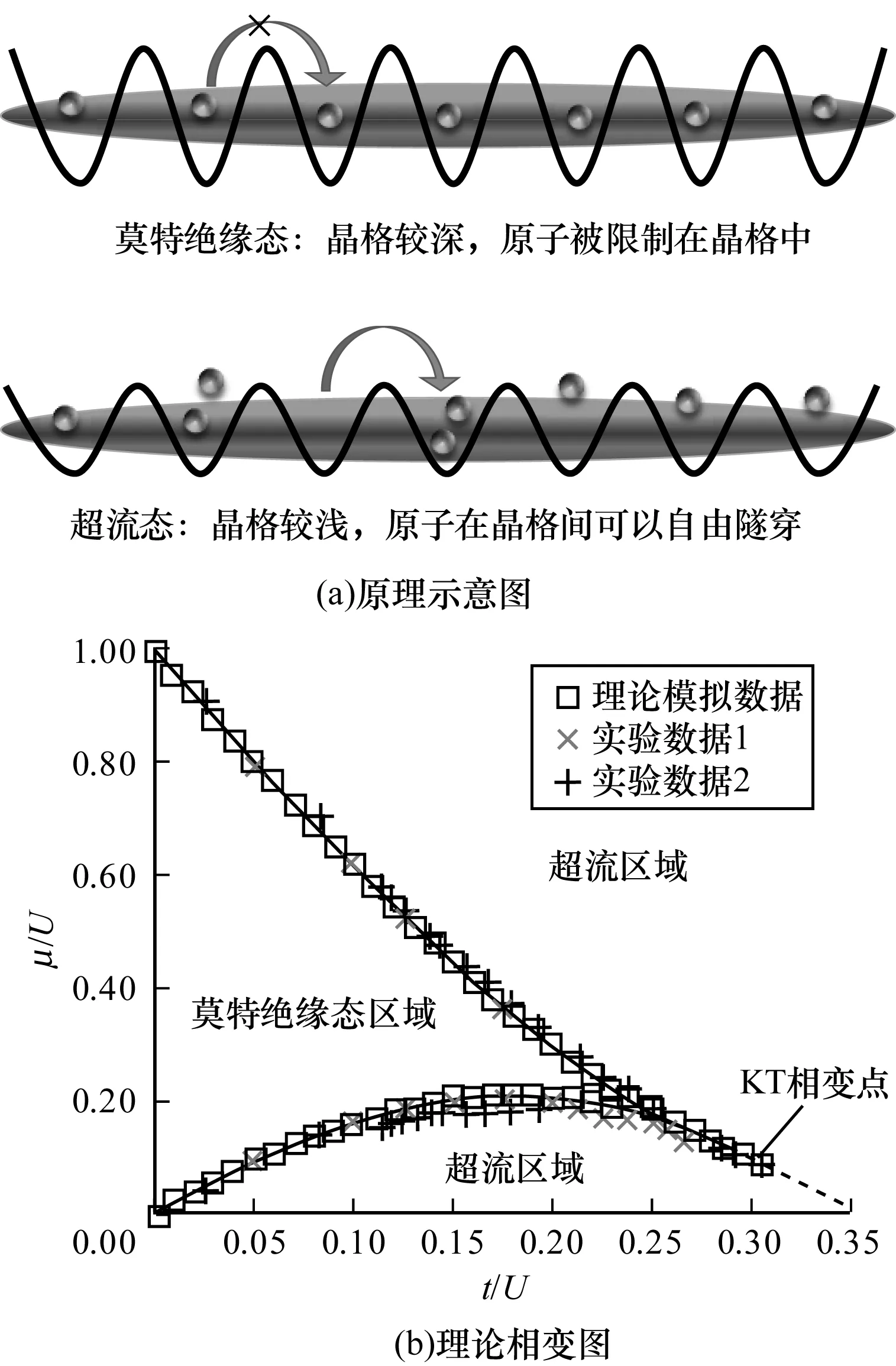
3 超冷原子的一维玻色-哈伯德模型

4 超冷原子超流-莫特绝缘态相变过程
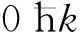





5 结束语

