基于量子五符号混淆信道模型的零错编码方法
李婧雅,余文斌,刘文杰,王金伟
(南京信息工程大学 a.江苏省大气环境和装备技术协同创新中心; b.计算机与软件学院,南京 210044)
0 概述
随着量子信息技术和量子计算机[1-2]的不断发展,越来越多的人开始进行量子计算和量子通信[3-4]。由于量子位[5]遵循量子力学规律[6],使其具有叠加态、纠缠态以及并行性等良好性能,因此,其在计算和通信速度上相较于经典计算和通信有着显著优势。另一方面,和经典通信一样,量子通信在信道环境中也存在噪声等影响通信质量的因素。在某些精度要求极高的通信中,这些噪声经常会导致严重后果[7]。在这种情况下,需要找到一种方法使得接收端接收到的信息可以零错区分,因此,零错信道的概念应运而生。
在经典零错信道[8]中,通信可以用N:X→Y表示。其中,X指信道输入的集合,Y指信道输出的集合。N(y|x)指输入为x时输出为y,对应的函数指出任意输入x和任意输出y之间可能的概率关系。香农所给出的零错信道概念指通过该信道传输的信息不会互相混淆,即不同信息需要满足当输入x不同时,通过函数N(·|x)得到的输出结果之间不相交。在经典零错信道概念被提出后,其容量上限被研究并产生了Lovász值的计算方法[9]。
近年来,对量子零错信道的研究主要集中在信道容量方面。文献[10-11]针对量子零错信道的可行性进行研究,发现在量子通信中零错信道依然可行。在确定了可行性后,需要找出量子零错信道容量的定义式并确定Lovász值,文献[12-14]对量子零错信道中的Lovász值进行研究并确定了其计算公式,然后给出关于无交互的量子零错信道容量。在此之后,文献[15]提出量子反馈信道Lovász值的计算方法。目前,针对量子零错信道编码的研究正处于起步阶段,文献[16]提出利用量子零错信道容量遍历相应矩阵的方法进行信源编码。
本文基于量子五符号混淆信道模型解决其相应的零错信道编码问题。回顾经典五符号混淆信道模型及其编码,建立与经典五符号对应的量子五符号混淆信道模型,然后利用量子叠加态特性,提出一种量子模型的零错信道编码方法,最后通过实例对比验证该量子零错信道编码方法的性能优势。
1 经典五符号混淆信道模型与编码
文献[8]提出的经典五符号混淆信道模型如图1所示。
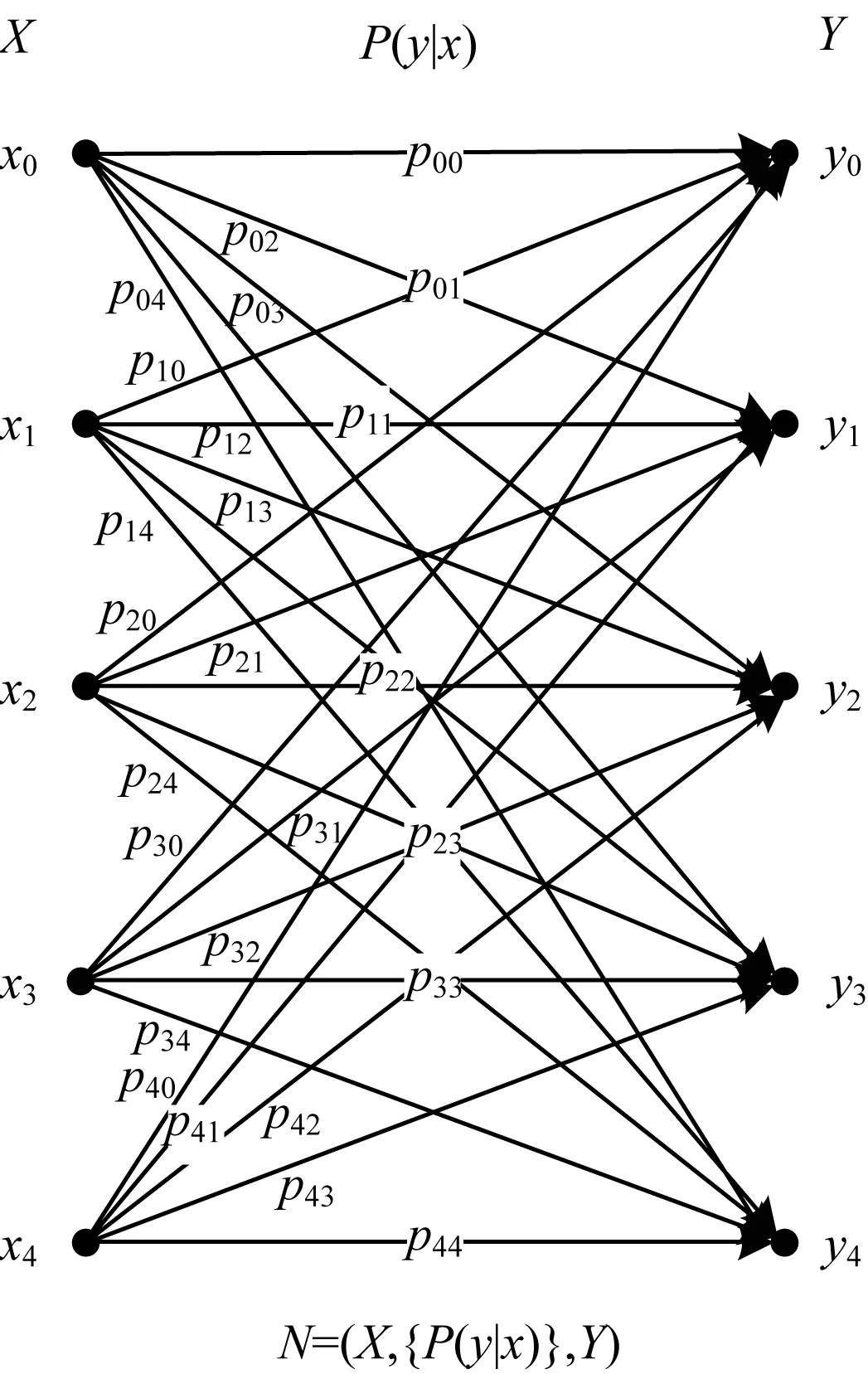
图1 经典五符号混淆信道模型
在图1中,输入方所传输信息用五符号表示,分别为x0、x1、x2、x3和x4,这5个符号信息通过上述信道后也得到5个输出,分别为y0、y1、y2、y3和y4。这5个输入分别转换成5个输出的概率用pij表示(i和j可以取0~4之间的任意正整数),例如,p03代表输入为x0、输出为y3的概率。根据信道特征可知,此处满足式(1)所示的条件。
(1)
其中,pij∈[0,1]。
(2)
在经典通信中,通过图的同构理论和矩阵向量相结合的方法确定信道的编码方式[9]。编码步骤如下:
步骤1由于在经典信道中,无论输入转换成对应输出的概率是多少,都会使输出结果混淆从而无法进行区分,这意味着信道中的概率对零错通信没有影响。因此,可以将图1信道中的概率去除,转化成图2所示的信道。
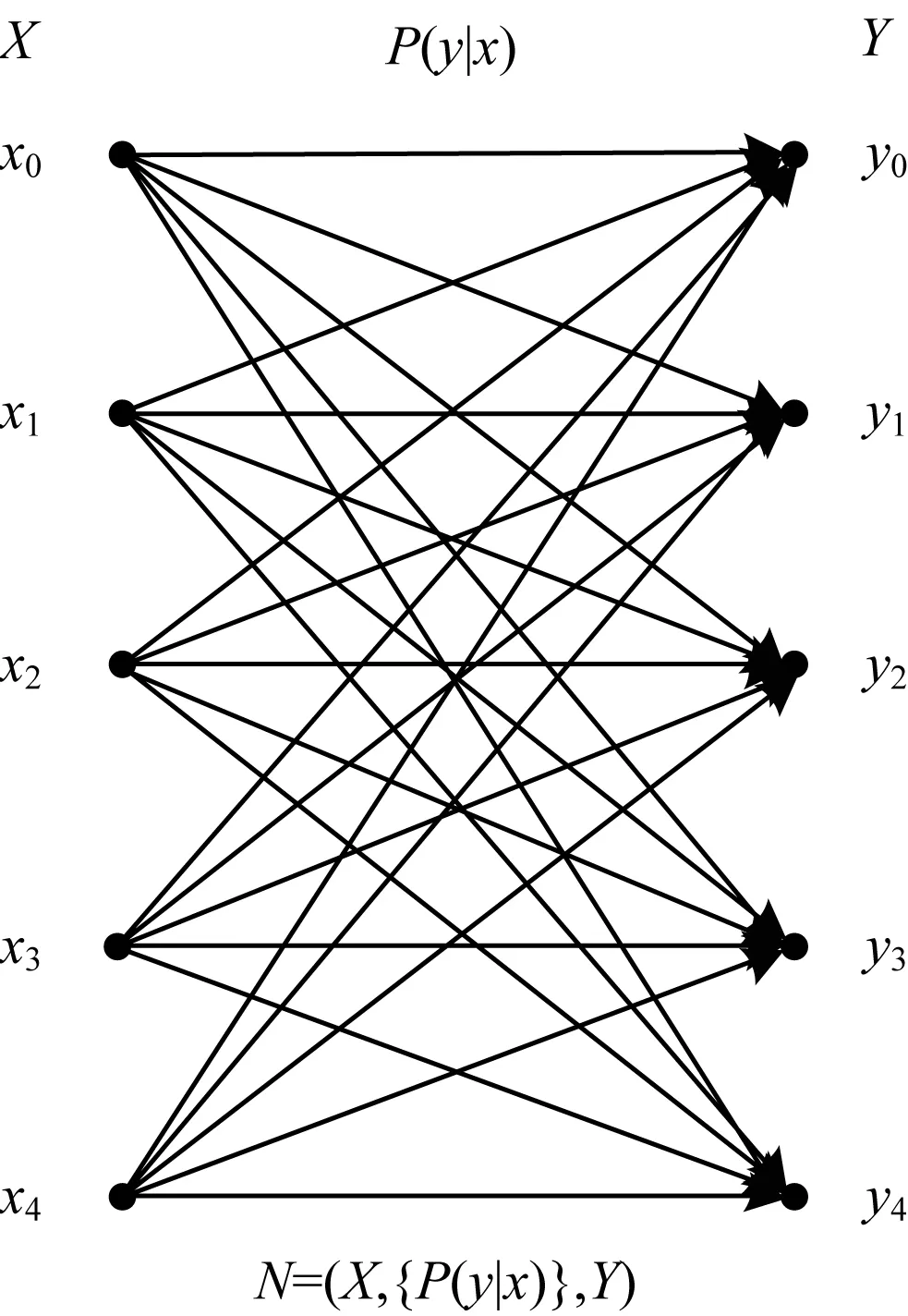
图2 经典五符号信道二分图
步骤2计算该信道的零错信道容量,即经典零错信道的Lovász值,以确定编码一位经典比特所需的码字位数。假设上述信道计算出的Lovász值为m,则需要m比特来进行编码。
步骤3通过图来确定编码方案。当需要m个比特进行编码时,从5m个可能输入中,找出对应输出集合不相交的5个输入,这5个输入即为编码。
例如,假定m的值为3,则可以先选择一个输入为000,再从10?(?代表0~4之间的任意正整数)中找输出集合不相交的输入,如果在10?中没找到,就从11?中找,直到找到与000输出集合不相交的输入为止。确定第1个和第2个输入后,再通过迭代找与第1个和第2个输出集合不相交的输入,直到找到所有输入,这些输入即是所要求的编码方案。
2 基于量子叠加态五符号混淆信道零错编码
2.1 量子五符号混淆信道模型
本文编码方法适用的信道模型,即量子五符号混淆信道模型如图3所示。
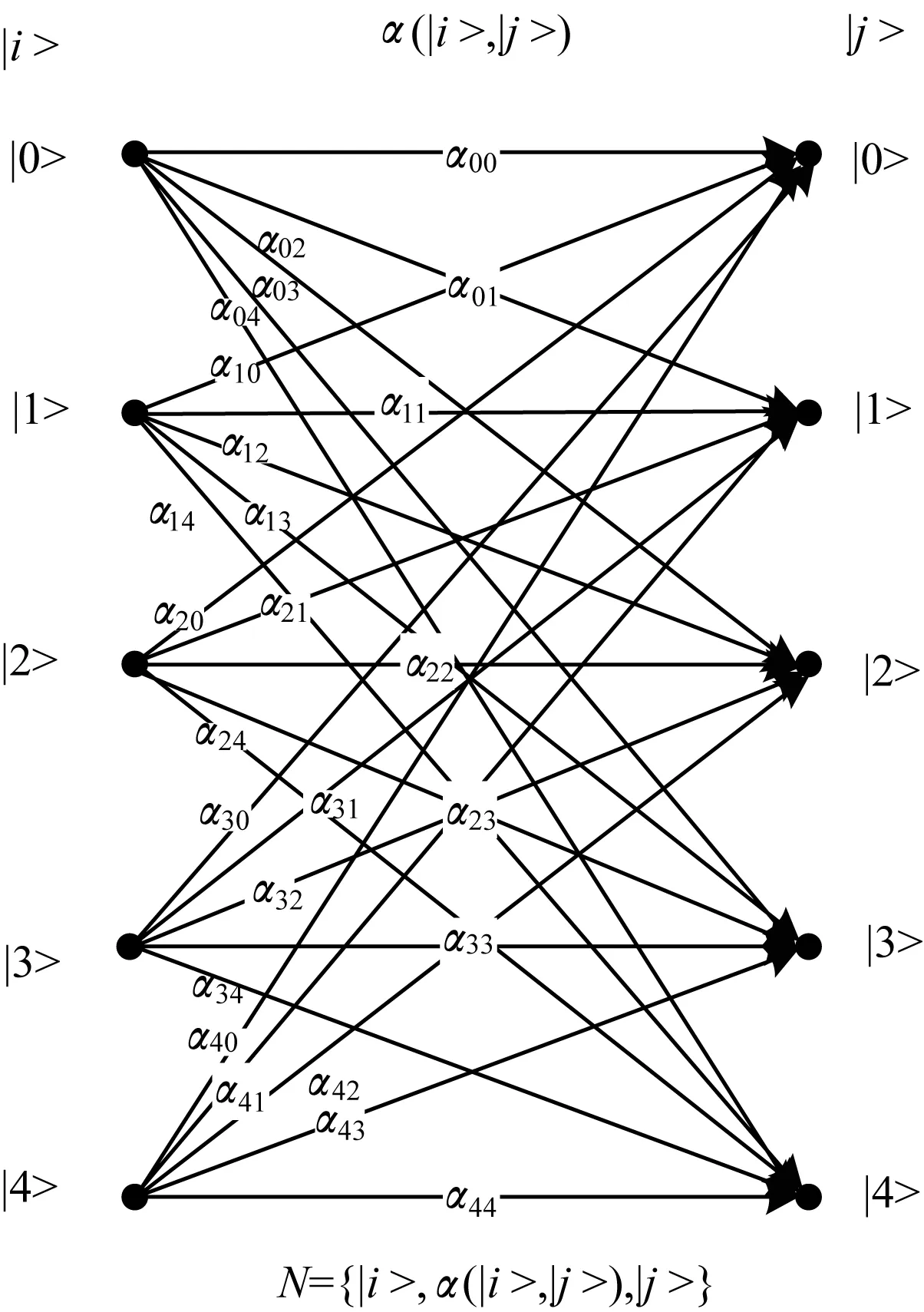
图3 量子五符号混淆信道模型
量子五符号混淆信道模型由3部分组成,分别为输入基态集合{|0>,|1>,|2>,|3>,|4>}、输出基态集合{|0>,|1>,|2>,|3>,|4>}以及输入基态集合和输出基态集合之间的系数关系,也即任意输入基态|i>(i∈[0,4]中任意正整数,下同)。通过该混淆信道后,形成叠加态:
(3)
其中,|j>表示输出基态中的任意基态,取值范围与|i>相同,αij是信道中的任意输入基态|i>与任意输出基态|j>对应关系的系数,例如输入基态|0>与输出基态|1>之间的关系可以用α01表示。αij满足以下条件:
αij∈[-1,1]中的任意复数
(4)
(5)
假设一个输入集合由k个叠加态组成,记为{|x0>,|x1>,…,|xl>,…,|xk>},其中,任意输入|xl>如下:
(6)
满足归一化条件:
(7)
将式(6)带入式(3)中,得到该输入通过信道后的对应输出为:
(8)
2.2 编码方法步骤
本文基于同构法的量子五符号混淆信道零错编码方法步骤如下:
步骤1将信道图转换为信道系数矩阵A。其中,系数矩阵表示如下:
(9)
系数矩阵中的任意值αij代表任意输入基态|i>到输出基态|j>的系数,与信道图中的αij一致。
步骤2计算该矩阵的线性无关向量组以及个数k,并且组成新矩阵C。算出5×5维的系数矩阵A的秩,记为k(k∈[1,5]中的任意正整数,下同),根据矩阵论相关知识,如矩阵消元法,可找出该矩阵中对应的k个5阶线性无关向量:
(10)
其中,l∈[0,k-1]。这k个线性无关向量和5-k个零向量组成一个新矩阵C:
(11)
步骤3确定系数矩阵A与矩阵C之间的关系。依据线性代数理论[16],C和A这2个矩阵之间总能找到一个如式(12)所示的矩阵B,使得式(13)成立。
(12)
AB=C
(13)
将式(9)和式(12)带入式(13)中,可得到矩阵C任意元素Cgf满足式(14)。
Cgf=α0fbg0+α1fbg1+α2fbg2+α3fbg3+α4fbg4=
(14)
由此可知,k个无关向量中的任意向量cl也可由式(15)表示:
(15)
步骤4利用同构向量确定输入、输出。通过上述矩阵求线性无关向量组的过程,可以得出实现量子信道零错的编码方案。在步骤3中,已经得出该信道的k个线性无关向量组。根据量子态与向量之间的同构性可知这k个线性无关向量(即k个输出)的量子态的矩阵形式。k个输出和对应的k个输入可以用式(16)和式(17)表示。
(16)
(17)
根据量子态可零错分辨的条件,任意2个态应当正交,他们之间的任意内积为0,即k个线性无关向量组应该满足:
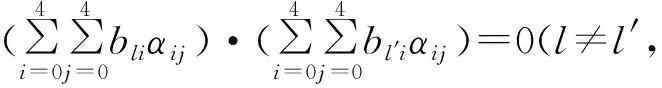
(18)
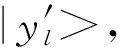
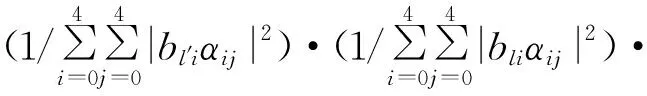
(19)
由此可证,任意2个输出之间可分辨。
3 实例对比与算法分析
3.1 实例对比
3.1.1 五符号邻边混淆信道
经典五符号邻边混淆信道和量子五符号邻边混淆信道分别如图4、图5所示。

图4 经典五符号邻边混淆信道
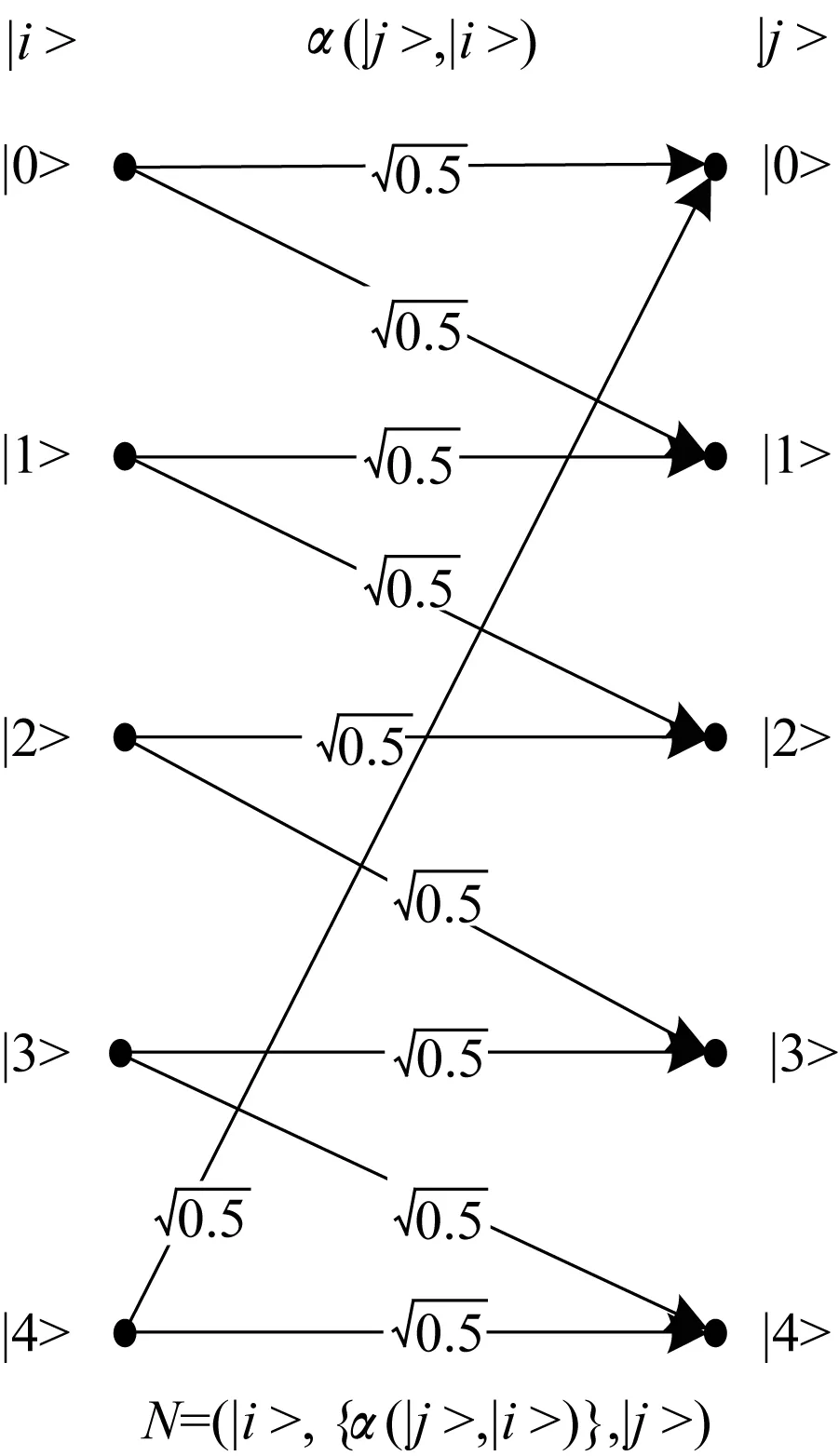
图5 量子五符号邻边混淆信道
分别按照前文提到的经典信道零错编码方法和本文量子信道零错编码方法,求解编码输入如下:

2)量子信道零错编码方法的5个输入为:
(20)
该方法一量子叠加态编码一位比特信息,信道容量为5。
3.1.2 五符号多边混淆信道
经典五符号多边混淆信道和量子五符号多边混淆信道分别如图6、图7所示。
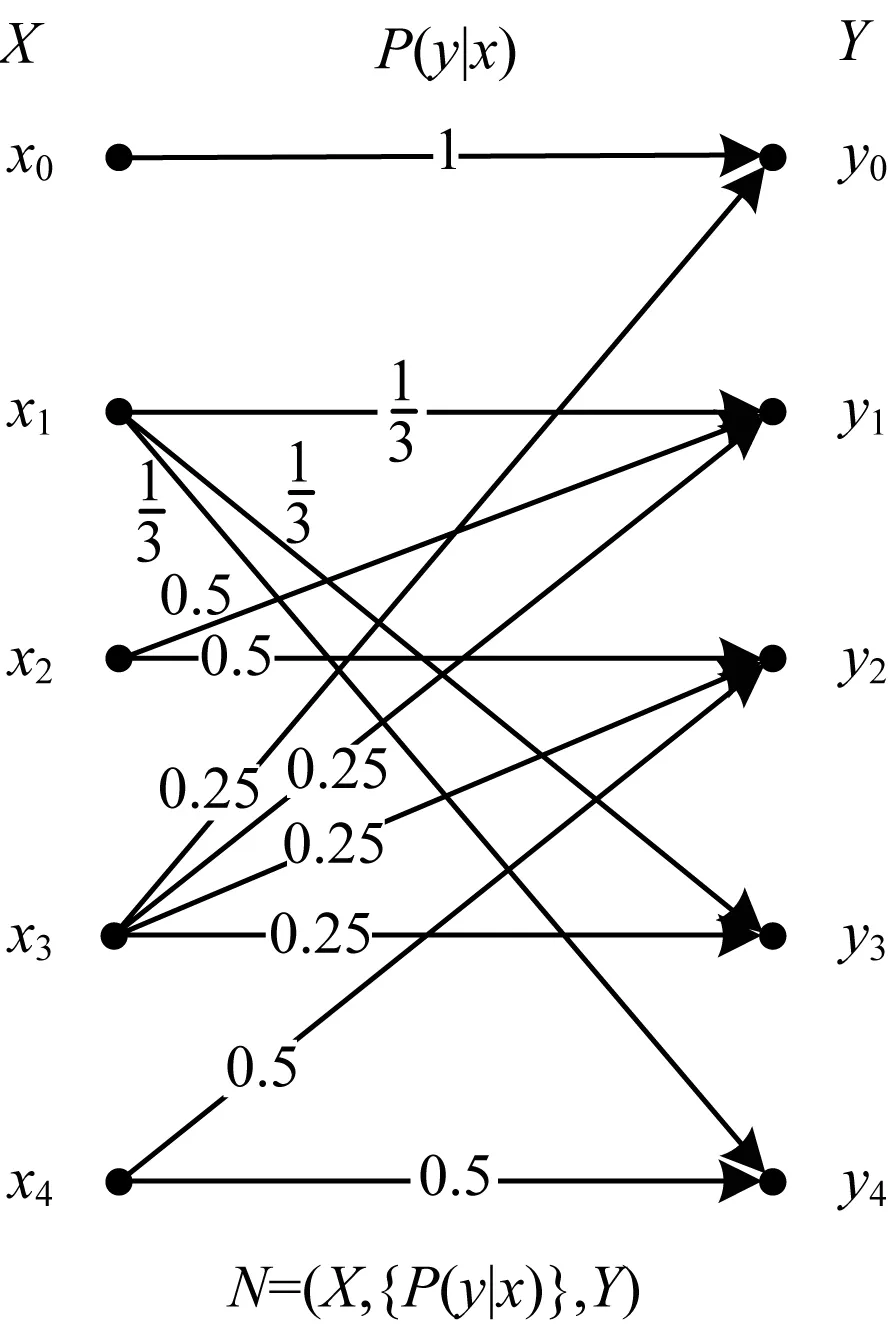
图6 经典五符号多边混淆信道

图7 量子五符号多边混淆信道
同样按照前文提到的经典信道零错编码方法和本文量子信道零错编码方法,求解编码输入分别如下:
1)经典信道零错编码方法的8个输入为:000,001,010,011,100,101,110,111,信道容量为2。
2)量子信道零错编码方法的4个输入为:
|x0>=|0>
|x3>=|4>
(21)
该编码方法的信道容量为4。
3.2 算法分析
定理1对于经典多边混淆信道,其零错信道容量CC 因此,CC 定理2量子多边混淆信道的信道容量CQ=d。 证明:由前文提出的线性变换算法可知,零错信道容量与所求解的可分辨向量组个数一致,且为信道矩阵最大线性无关向量组的个数,即系数矩阵的秩d。 因此,CQ=d。 定理3经典多边混淆信道的编码算法复杂度大于等于O(2n),其中,n为信道矩阵的维数。 证明:根据文献[5]的编码算法和本文第2节的分析可知,经典信道零错编码分为2个部分: 1)计算Lovász值,这需要多次遍历矩阵空间,其算法复杂度大于等于O(2n)。 2)采用遍历算法搜索码字空间,求得具体的码字。设Lovász值为θ,则遍历次数为nθ,故其复杂度为O(nθ)。 因此,经典多边混淆信道的编码算法总体复杂度大于等于O(nθ+2n),即大于等于O(2n),该算法是一个NP问题。 定理4量子多边混淆信道的编码算法复杂度为O(n2)。 证明:量子信道零错编码的算法复杂度为4个独立步骤复杂度的总和。步骤1和步骤4的算法复杂度是n,步骤2和步骤3的算法复杂度是n(n-1)/2。由此可知,算法总的复杂度为: (22) 由定理1和定理2可知,量子信道容量CQ大于经典信道容量CC。另一方面,由定理3和定理4可知,量子零错编码方案的算法复杂度仅为O(n2)。这意味着在相同条件下,采用量子通信的方式可以传递更多的零错信息并具有更快的编码速度。因此,本文提出的量子信道零错编码方法相较于经典方法具有更高的编码效率。 本文提出基于量子叠加态的五符号混淆信道零错编码方法。该方法利用量子叠加态与向量之间、信道与矩阵之间的对应关系以及矩阵和向量的转化关系,实现在量子五符号混淆信道下的零错信道编码。分析结果表明,相较于经典信道编码方法,该方法具有更高的信道容量和编码效率。本文虽然总结了编码的理论推导式,但具体编码线路仍有待确定,解决该问题将是今后的研究方向。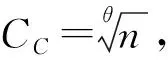
4 结束语

