数据驱动的自适应容错技术研究
刘睿涛,陈左宁
(1.数学工程与先进计算国家重点实验室,江苏 无锡 214215; 2.国家并行计算机工程技术研究中心,北京 100190)
0 概述
超级计算机性能的提升带来了系统规模的不断增大。其中,10P量级高性能计算机的规模目前已经达到数万处理器规模。不断增加的系统规模与复杂度,在高性能计算领域带来了巨大的可靠性挑战。据估算,E量级高性能计算机的平均无故障时间只有30 min左右[1-3]。针对超级计算机的故障特征,科研人员进行了相关研究,对以蓝色基因系统为代表的多个大型系统的故障分析,建立了初步的故障特征模型,但其中有些研究的故障类型较少[4-6],还有些研究的故障单元粒度较粗[7-9],缺乏对超级计算机全面的细粒度故障分析。目前,研究人员对Taitan超级计算机的大规模GPU故障进行了分析,但由于缺乏精确的故障时间信息,其分析只能以24 h为最大时间精度[10]。
为解决系统可用性问题,基于检查点/重启的容错技术得到广泛应用。研究人员通过对系统故障建模,并对检查点进行了优化,但未从应用运行模式上进行失效模型的分析[7]。近年来,随着故障预测研究的不断深入,并取得一定进展[11-15]。但是,超级计算机的容错由于未能与系统的实际可靠性数据相结合,在大规模并行应用上未获得最佳的运行效率。此外,由于超级计算机越来越高的复杂度,指数分布的故障模型是否适应P级超级计算机,可应用以此为依据导出的检查点间隔优化策略[16],需要结合超级计算机进行分析。
根据实际运行环境的可靠性对检查点时机进行优化,指导系统级或应用级检查点的执行,可有效降低检查点开销,提升超级计算机的可用性。本文以神威太湖之光系统为研究主体,分析该超级计算机中复杂多样的系统故障,建立了面向超级计算机复杂故障的部件级和应用级失效模型,并以该模型为基础,给出数据驱动的自适应容错模型,设计自适应优化算法。
1 故障分类与采集方法
1.1 神威太湖之光系统
神威太湖之光计算机系统是一台数十亿亿次(100 petaflops)级超级计算机,能有效支持计算密集型、通信密集型和I/O密集型应用。该系统包括40 960个CPU,每个机仓由4个运算超节点组成。每个超节点包括32个运算插件卡和1个网络背板。每个运算插件卡上集成8个CPU和1个集成网络卡。CPU节点采用异构众核处理器,片上集成260个异构核心,采用计算阵列和分布式共享存储相结合的异构众核体系结构。CPU节点配置大容量DDR3-2133存储器芯片,采用PCIe 3.0接口,提供高带宽系统数据交换能力。太湖之光系统的组织结构如图1所示。

图1 太湖之光系统组织结构
1.2 数据采集与故障分类
1.2.1 数据采集
太湖之光通过一套覆盖包括主机计算系统在内的全系统监控与维护诊断基础设施进行全机主要目标的监控、诊断与维护。分布式故障采集框架如图2所示。

图2 分布式故障采集框架
该基础设施主要包括维护BMC(Base Board Management Controller)、运算维护板PM(Processor Management)、顶层网络维护板TNM(Top Net Management)及监控软件。
维护BMC用于实现对插件内CPU及其主存、HCA芯片的维护和监控。BMC是维护系统的最基础部件,向下提供多条并行维护通道与被维护的器件连接,向上与维护管理网络互连,构成可伸缩的维护系统。运算维护板(PM)位于运算中板的背面,每个运算底板一块,用来实现对中板内所有计算网络插件(CN)、运算节点BMC、以太网交换板等目标的管理、监控。
借助分布式的故障采集框架,在太湖之光系统上设置了以下故障传感器:
1)CPU节点故障传感器;
2)IBA卡故障传感器;
3)电源故障传感器;
4)温度传感器;
5)软件传感器。
传感器设置和数据采集覆盖了全部计算单元。通过故障采集框架,对分布于系统的传感器获取的数据进行在线实时存储,建立系统的故障分析大数据集。
故障传播会导致故障之间的相关性,对故障分析带来影响[17-19]。为了确保能够获得真实故障源,避免故障传播,太湖之光系统采用了软硬件协同设计方法。基于硬件设计,在CPU节点和其他主要部件上采用了主动与被动隔离设计。例如,当计算核心检测到自身发生不可纠错或故障时,将主动进行自我隔离,主要包括阻止该计算核心到其他部件的请求、丢弃该计算核心的响应。故障部件也可以通过软件设置进行隔离。在软件设计上,当部件的不可纠错或故障被检测到时,软件基础架构对相关的应用进行容错处理,并对故障部件立即隔离。
1.2.2 故障分类
故障记录主要包括故障主体(CPUID,COREID)、故障标识(FAULT_TYPE_ID)、故障名称(FAULT_NAME)、发生时间(OCCUR_TIME)、实时温度(CPU_TEMP)、故障现场(FAULT_SCENE)等项目。故障主体描述故障发生目标,包括CPU核心、CPU控制部件、内存、HCA、电源、维护部件等。故障标识和故障名称涵盖了CPU主核与从核故障、CPU控制部件故障、内存故障、HCA故障、维护部件故障、供电部件和冷却部件故障等详细故障类型。发生时间记录了故障发生的时间(精确到秒级)。CPU温度记录了故障发生时CPU的实时温度。故障现场记录了故障的详细现场信息。
为了对故障进行统计分析,根据系统结构和组装特征,将各类详细故障类型归类为CPU故障(不包括DRAM内存)、内存故障、CPU节点故障(包含CPU和DRAM)、计算插件卡故障、互连设备故障、维护设备故障、电源设备故障和冷却设备故障等故障大类,每个故障大类又根据部件微结构进一步细分为详细的故障类型。例如内存故障细分为内存单错和内存多错故障等,CPU故障细分为各计算部件故障和相关控制部件故障等。
根据故障严重程度和处理方式,每个故障又分为非严重故障和严重故障。非严重故障是指不会导致系统失效的非正常状态或可由硬件自行纠错的非正常状态(例如,可纠正的DRAM单错)。严重故障是指立即会导致系统失效的非正常状态或必须由软件系统进行容错干预的非正常状态。
太湖之光系统有170多个详细故障类型,其中导致主机系统失效的严重故障有108类。
1.3 数据预处理
数据预处理是指对故障进行分类和过滤、优化故障分析以及提升分析效率[20]。
在大规模并行计算机运行中,失效是指系统在遇到某些故障时,无法通过硬件自身的自动容错机制进行在线修复并继续运行。对非严重故障,硬件系统可以通过纠错机制自动恢复(例如ECC检纠单错)。对严重故障,则无法自动修复,此时系统会中断正常运行,造成系统失效,需要在带外系统和软件的干预下进行容错和恢复。系统失效由严重故障引起,因而在进行失效时间分析时,需过滤掉非严重故障。
本文数据预处理是对原始故障记录进行排重和过滤,保留与失效有关的严重故障,避免信息丢失,确保失效分析有效性,以加速分析过程。
数据预处理包括3步:1)过滤掉在线故障记录中的不合格记录,例如带有空缺项记录(空缺项记录很少,主要由监控程序异常造成);2)对重复数据进行去重,例如同一时刻同一目标的相同故障记录,借助数据库sql查询技术,实现数据去冗;3)根据故障分类及等级选取所需故障类型,筛除不相关故障。
本文选取太湖之光系统3年时间(2014-07-01—2017-07-01)的故障数据作为数据源。经过数据预处理,可将分析数据压缩至原始数据的13%,如图3所示。
2 面向复杂故障的多层失效模型
2.1 细粒度失效分布模型
从时间上对故障进行量化分析,可以定量描述故障分布,掌握系统动态可靠性特征,为容错优化提供基础。
从图4可以看出,系统对可靠性影响最大的是主机计算系统(主要包括CPU、内存和互连系统等)。本节以太湖之光主机系统的CPU节点为基本部件单元,在不同时间区间上分析其失效间隔时间,并建立细粒度失效分布模型。
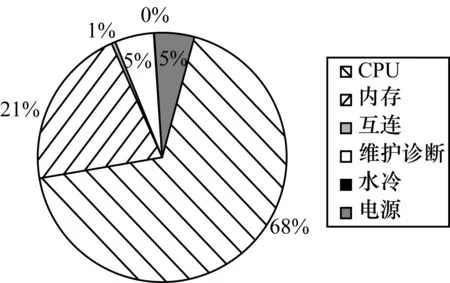
图4 太湖之光故障分布模型
1)分析方法
指数(Exponential)分布(T~E(λ))、对数正态(Lognormal)分布(T~LN(μ,σ2))、Weibull分布(T~W(m,η))和Gamma分布(T~Γ(α,λ))是具有代表性的几种寿命分布[21]。4种分布的密度函数如表1所示。

表1 典型寿命分布
本文选用上述数学模型,按照划定的时间区间,在相同时空维度上对比分析系统内各基本故障单元的失效时间特征。 通过最大似然估计法,采用累积失效分布数据对候选分布参数进行拟合。然后使用Kolmogorov-Smirnov检验候选分布与实际数据符合度,产生的P值作为模型拟合度评估标准。P值越低,符合度越差;反之,则越好。一般要求P值大于阈值0.05,才认为该分布与实际数据符合。
2)太湖之光失效时间分析
根据实际失效数据,本文绘制了太湖之光系统中随机选取的2个CPU节点在不同时间区间上的失效间隔时间分析(图5)。其中,实线曲线表示实际失效间隔时间数据,其他虚线曲线分别对应拟合的Weibull、Gamma和对数正态分布,图5(a)、图5(d)为第1时间区间(2014-07-01—2015-07-01),图5(a)、图5(e)为第2时间区间(2015-07-01—2016-07-01),图5(c)、图5(f)为第3时间区间(2016-07-01—2017-07-01)。
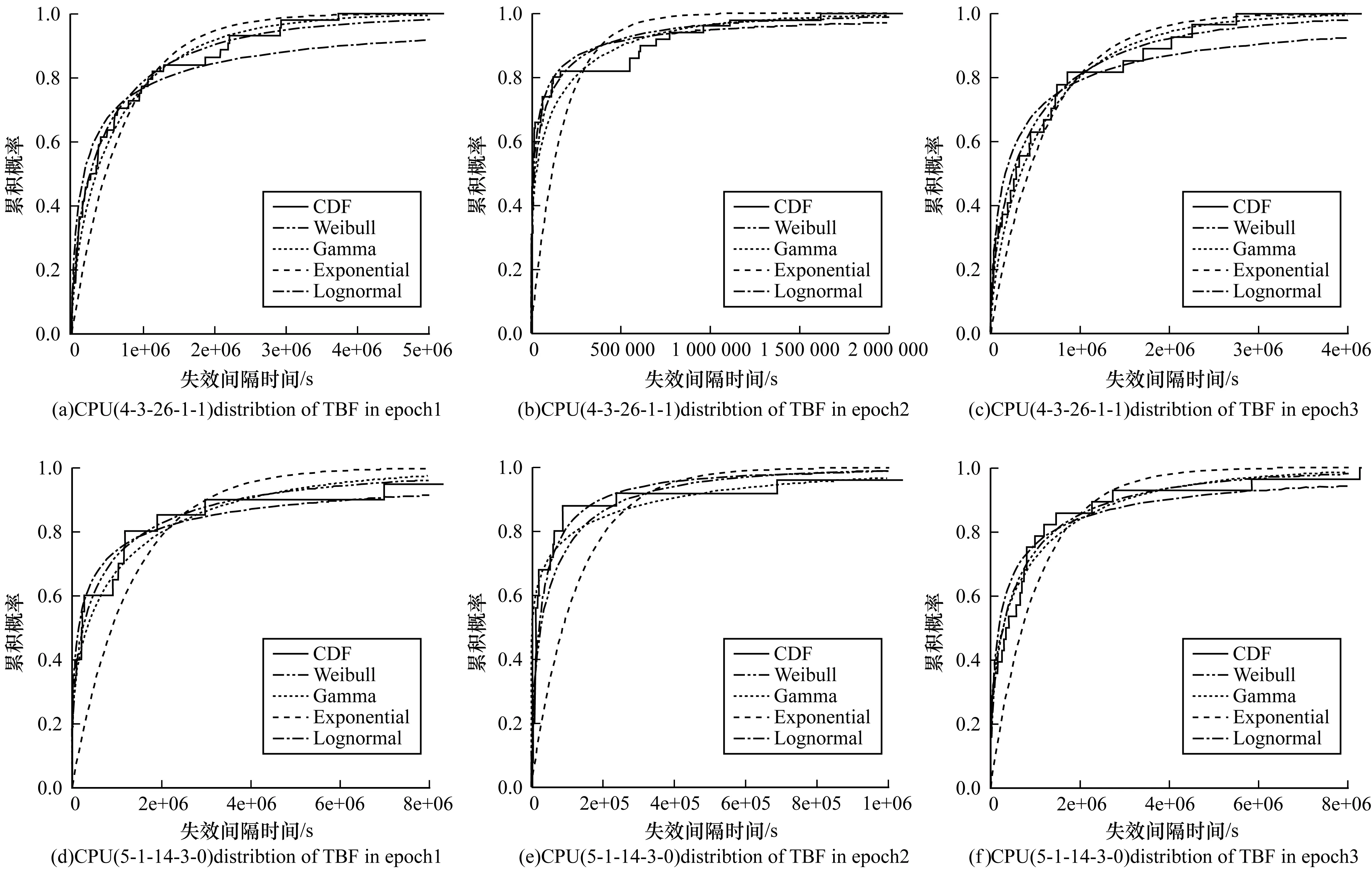
图5 不同时间区间的失效间隔时间分布示例
从图5可以看出,在3个不同时间区间上,指数分布模型是与CPU节点的实际失效数据最不符合的分布,Weibull、Gamma和对数正态分布与实际失效数据符合度较好。
表2是随机选取的2个CPU节点失效间隔时间分布参数与拟合度分析。与真实故障数据对应的对指数分布、对数正态分布、Gamma分布和Weibull分布参数及Kolmogorov-Smirnov检验产生的p值在表中列出。
以CPU节点(4-3-26-1-1)为例:
在第1时间区间内,指数分布的K-S检验p-value=0.017 665 46,小于通常的分布检验符合度标准0.05,与实际失效数据不符合;Weibull、Gamma和对数正态分布分布都符合实际失效数据,Weibull符合度最好(p-value=0.912 390 5),其次是Gamma(p-value=0.779 198 4),最后是对数正态分布(p-value=0.179 714 3)。
在第2时间区间内,指数分布和Gamma分布与实际失效数据不符合(指数分布的p-value=4.229 95e-14,Gamma分布的p-value=0.046 696 84),对数正态分布符合度最好(p-value=0.668 755 8),其次是Weibull分布(p-value=0.149 518)。
在第3时间区间内,这4个分布与实际失效数据都符合,符合度最好的是Weibull分布(p-value=0.990 419 4),其次是Gamma分布(p-value =0.722 965 8)和对数正态分布(p-value=0.462 257),最后是指数分布(p-value=0.149 760 3)。
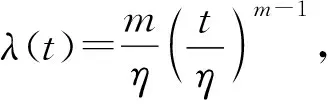

表2 太湖之光失效分布及参数
此外容易发现,在CPU节点(4-3-26-1-1)上,虽然Weibull分布与实际失效间隔时间符合度最好,但不同时间区间上,其Weibull分布参数有较明显差异(第1时间区间,m=0.592 533 5,寿命特征η=476 345.9;第2时间区间,m=0.405 037 4,η=50 703.25;第3时间区间,m=0.623 815 7,η=446 174.6)。这说明同一个部件的失效分布模型参数随着时间也在不断变化,并且CPU节点(4-3-26-1-1)在3个时间段上的故障数也不同。进一步深入分析发现,在这3个时间段上,该CPU的负载有不同的特征。
同样,对表2另一个CPU节点失效数据的拟合分析显示,Weibull分布与实际失效间隔时间符合度最好,可以用于定量描述故障单元的失效间隔时间。并且发现相同类型不同位置的故障单元之间,与其失效间隔时间对应的Weibull分布的参数也不相同。
对太湖之光系统不同粒度的所有故障单元进行分析显示,Weibull分布与故障单元的实际失效数据符合度最好,并且在不同的时间区间内,其形状参数和寿命参数都不同。这说明虽然同一个部件的失效分布模型可以用Weibull分布进行描述,但根据故障单元运行负载的变化,分布参数也会随之变化。
3)结果分析
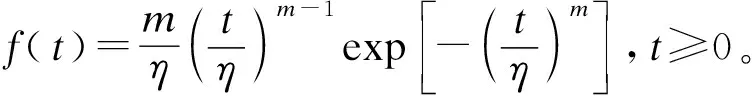
(1)同一部件随着时间或负载的变化,与其失效时间对应的Weibull分布参数不断变化。
(2)类型相同但位置不同的部件,与其失效时间对应的Weibull分布参数不尽相同。
(3)同一部件在不同时期的故障率(或故障数)不同。
2.2 应用级失效模型
并行应用规模用计算单元(计算单元以CPU节点为基本单位)数量进行定量描述。可以做如下合理假设:在并行应用运行过程中,所有计算单元的故障之间独立。事实上,通过1.2.1节分析可知,该假设合理。
在大规模并行系统中,并行应用的各个任务之间关系一般有2种:强相关性和弱相关性。强相关性是指并行应用的任务之间有相互依赖关系,在任务的不同阶段需要进行交互。弱相关性是指并行应用的任务之间基本无依赖关系,无交互关系。
对于具有任务强相关性的并行应用,在任何一个任务或其运行部件发生失效时,将影响到整个并行应用,一般需要检查点重启机制重新部署并行应用。对于具有任务弱相关性的并行应用,在任何一个任务或其运行部件发生失效时,根据容错模式可以采取降级运行,删除失效任务,或者重新部署失效任务,使其恢复运行,都不会影响并行应用中的其他任务。
对于任务强相关性的并行应用,只要该应用使用的计算单元之一发生了严重故障,就会导致该应用运行中断。因此,在分析这种并行应用的失效模式时,采用其所使用计算单元的串联模型。
对于任务弱相关性的并行应用,可将其视为与独立任务一一对应的多个应用。以独立任务为单位,分析失效模型。
1)任务强相关性并行应用失效模型
应用规模用N表示,Fjob(N,t)表示规模为N的应用在t时刻之前失效的概率,Fnode(N,t)表示个数为N的计算单元集合在t时刻之前发生失效的概率,Fi(t)表示计算单元i在t时刻之前发生失效的概率。那么有:
(1)
规模为N的任务强相关性应用的故障概率模型如图6所示。
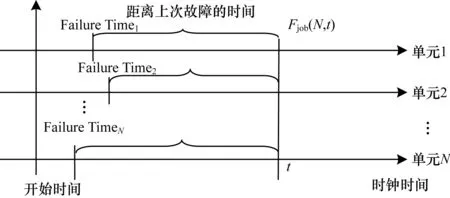
图6 规模为N的强相关性应用失效模型
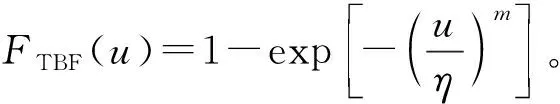
若ftimei是计算单元i的上次发生故障时间,则有:
Fi(t)=FTBF(t-ftimei)=
(2)
其中,t≥ftimei,t为时钟时间,ftimei是计算单元i的上次发生故障时间或开始运行的时间。
从而式(1)演变为:
(3)
(4)
其中,t≥max(ftime1,ftime2,…,ftimeN),Fjob(N,t)是应用的可靠性分布函数,fjob(N,t)是应用的失效概率密度函数。至此,应用级失效分布模型建立,可据此进行应用的可靠性和容错优化分析。
规模为N的应用平均无故障时间为:
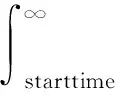
(5)
从失效分布模型可以看出,该模型与几个参数密切相关,包括应用规模N、应用启动时间starttime、各计算单元上次故障发生时间ftimei、各计算单元的形状参数mi和寿命分布参数ηi,如表3所示。

表3 应用失效模型参数及含义
在应用运行过程中,应用的平均无故障时间可以根据式(5)进行计算。但注意到在应用发生了故障之后,发生故障的计算单元的ftimei相应发生变化。另外,从2.1节分析发现,计算单元的失效分布模型参数(mi和ηi)也随时间或负载而变化。可见,应用失效分布模型是动态变化的。
2)任务弱相关性并行应用失效模型
将并行应用按照独立任务进行拆解,以独立任务为单位,分别建立失效模型。独立任务的失效模型与任务强相关性并行应用一致。
3 数据驱动自适应容错
本节分析任务强相关性并行应用。对于任务弱相关性并行应用,可将并行应用按照独立任务进行拆解,然后以独立任务为单位,优化任务强相关性并行应用的自适应容错方法。
3.1 检查点模型及优化
在任何采用检查点/重启技术的容错系统中,都需要在检查点开销与计算开销之间取得平衡,以实现最低开销下的容错。过于频繁或者过长的检查点间隔都会导致系统容错开销或丢失的计算量增大,一个最优的检查点策略才能尽量降低检查点开销,提高容错效率。
一般地,检查点相关的参数包括检查点保留开销、检查点间隔时间(或计算时间)、检查点恢复开销、因故障损失的计算时间等,检查点参数如表4所示。

表4 检查点参数及含义
典型的检查点时序模型如图7所示。对应用进行检查点容错的过程如下:应用开始执行(starttime),并运行一段时间(持续Tc),之后进行一次检查点保留(开销Ts),之后循环往复执行上述过程。当应用相关的软硬件资源发生失效(或严重故障)时(丢失计算量Tl),执行检查点恢复(开销Tr),并从检查点处继续开始执行,依次类推。
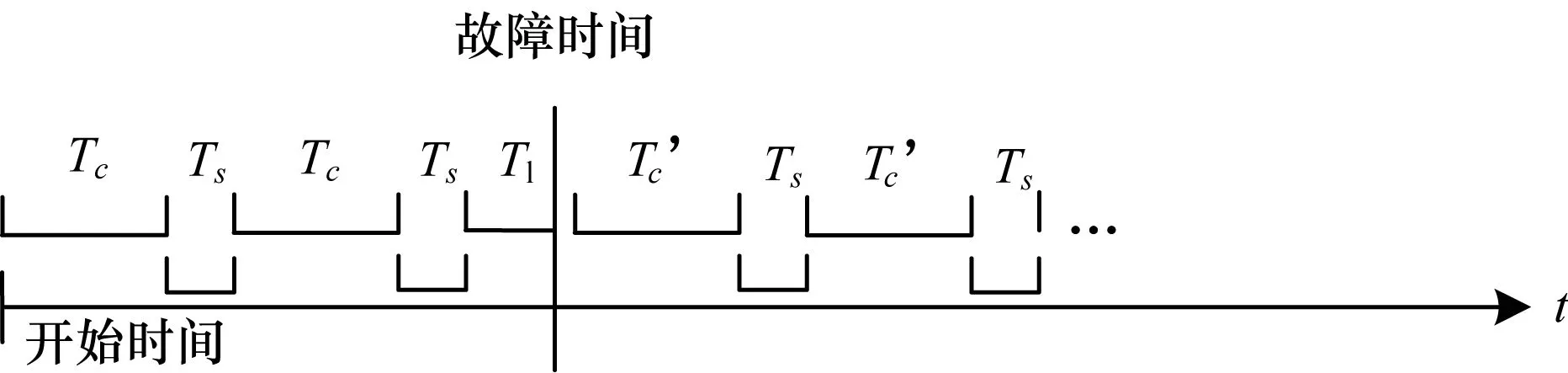
图7 作业检查点时序模型
一般地,在大规模并行系统中,应用恢复时间相比计算时间和检查点时间开销非常小,在此处检查点优化分析中可以忽略不计。
当应用的故障发生时间T在[starttime+n(Tc+Ts),starttime+(n+1)(Tc+Ts)],n=0,1,…之间时,那么没有用于计算的时间Tw=T-starttime-nTc。Tw是检查点容错的开销,包括用于检查点的时间和故障发生时丢失的计算时间。
根据应用级失效分布函数,可以得到Tw的期望值(即平均检查点容错开销):
fjob(N,t)dt
(6)
当E(Tw)达到最小时,可以认为应用的检查点容错开销最小。在应用规模确定后(N和Ts是常量),目标是寻找合适的Tc使得E(Tw)达到最小。这归结为一个数学最优化问题。本文采用最优化方法和应用数学包来解决寻找最优化Tc的问题。
3.2 动态自适应的检查点优化
在检查点间隔优化模型中,注意到应用的失效概率密度函数f(t,N)参数中的ftimei,在应用启动后未发生故障的时间段内,可以用初始的参数值ftimei来计算Tc的最优化解。但应用发生了失效并重新启动运行后,发生故障的计算单元的ftimei就要相应地进行修正。因此,基于检查点时序模型的优化策略,在应用发生失效之前,存在一个最优检查点间隔;当应用发生失效后,需要更新应用失效分布中故障计算单元的失效时间参数ftimei,并重新计算最优检查点时间间隔,如图8所示。此外,从细粒度失效分布模型分析可以发现,随着系统负载的变化和时间的推移,计算单元的失效分布模型参数(mi和ηi)也随之变化。计算单元失效分布参数的变化,说明应用的失效分布是一个动态变化的模型,随着系统实际运行进行动态变化。
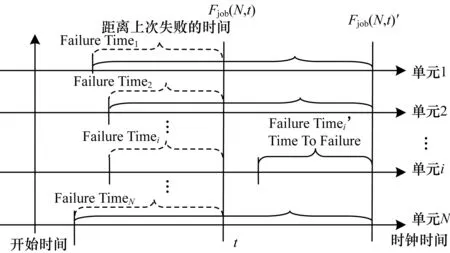
图8 动态作业失效模型
综上所述,检查点间隔优化是一个动态更新过程,该过程具有自适应特征。
计算单元故障发生时间(ftimei)的调整,可以用系统记录的严重故障发生时间直接替换即可。而失效分布参数(mi和ηi)的调整,本文采用基于p值的自适应优化方法进行动态调节。
计算单元分布参数的调整,采用基于p值的自适应分布模型参数优化算法(算法1)。随着故障采样窗口的移动,以Kolmogorov-Smirnov检验的评估参数p-value作为标准,动态地对失效模型的参数进行修正,提高失效分布模型的准确度。
算法1基于p值的自适应分布模型参数优化
输入计算单元i的拟合窗口宽度width,当前发生故障时间ftime,最近故障数据历史采样ftime1,ftime2,…,ftimewidth-1,最近拟合的Weibull分布参数mi和ηi
输出计算单元i的最新优化Weibull分布参数mi和ηi
步骤1need_refresh=false;
threshold = 0.5;
步骤2IF 参数mi和ηi为0(说明是第一次计算分布参数或者需要重新更新分布参数)
THEN
选取最近的width个严重故障发生时间采样数据,采用最大似然估计法计算weibull分布的参数;
ELSEIF 参数mi和ηi都不为0
THEN
need_refresh = true;
步骤3采用kolmogorov-smirnov检验,检验最近width个故障采样与weibull分布拟合度,得到p-value。
IF((p-value > threshold)‖(need_refresh==false))
THEN
输出参数mi和ηi;
ELSE IF (need_refresh == true)
need_refresh = false;
置参数mi和ηi为0;
GOTO 步骤2;
算法1的主要思想是通过对严重故障发生时间的采样,利用最大似然估计法得到计算单元的分布参数。在出现新的故障后,视情况动态调整分布参数。采用Kolmogorov-Smirnov检验来评估是否需要重新调整分布参数。如果p-value表明基于原来参数的分布与最新故障采样符合度达到要求,则无需调整分布参数;否则,采用最大似然估计重新计算分布参数。
4 实验结果与分析
4.1 实验环境
本文选取太湖之光系统的一个机仓(4机仓),以实际故障为依据,分析检查点优化的策略及效果。故障数据采集周期为1 a。在该周期中,系统运行以计算密集型课题为主,兼顾访存、通信和IO密集型课题。检查点优化过程如图9所示。
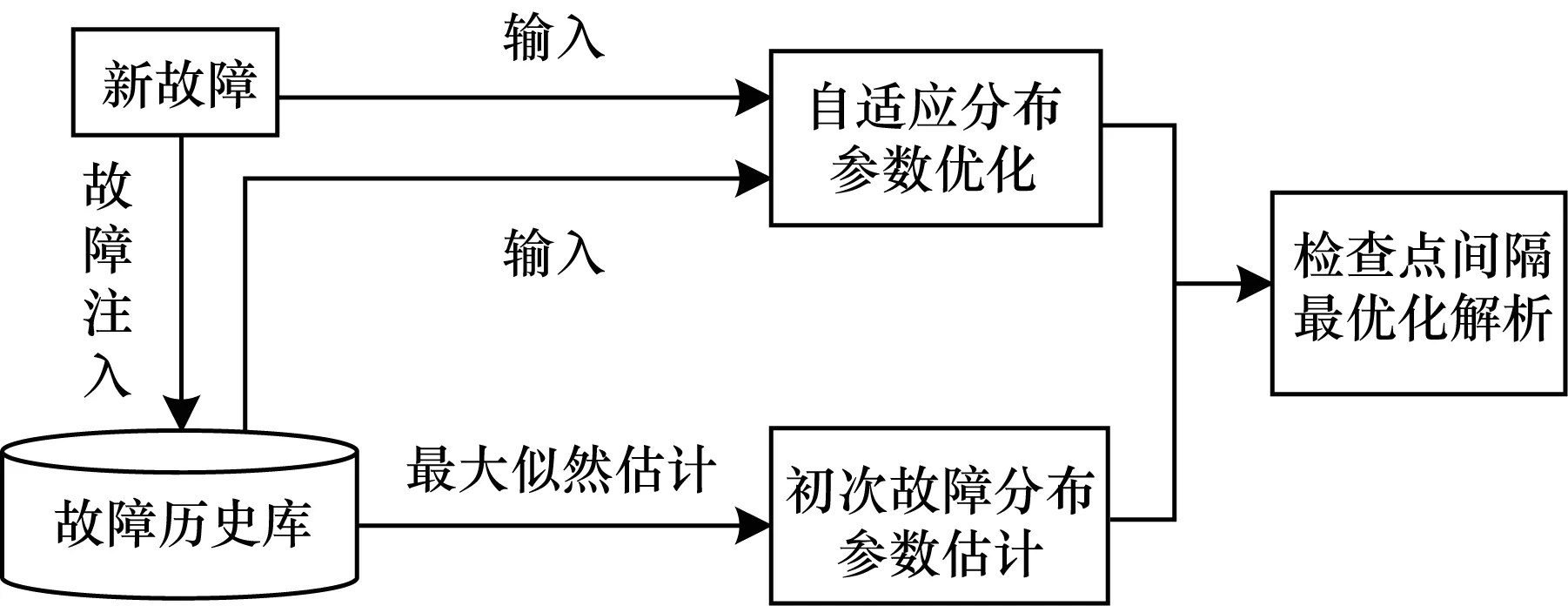
图9 自适应检查点优化
表5是根据故障历史数据计算得到的CPU节点的初始Weibull分布参数(K-S检验p-value值都大于0.5)。从表5可以看出,CPU节点之间的可靠性存在显著差异。
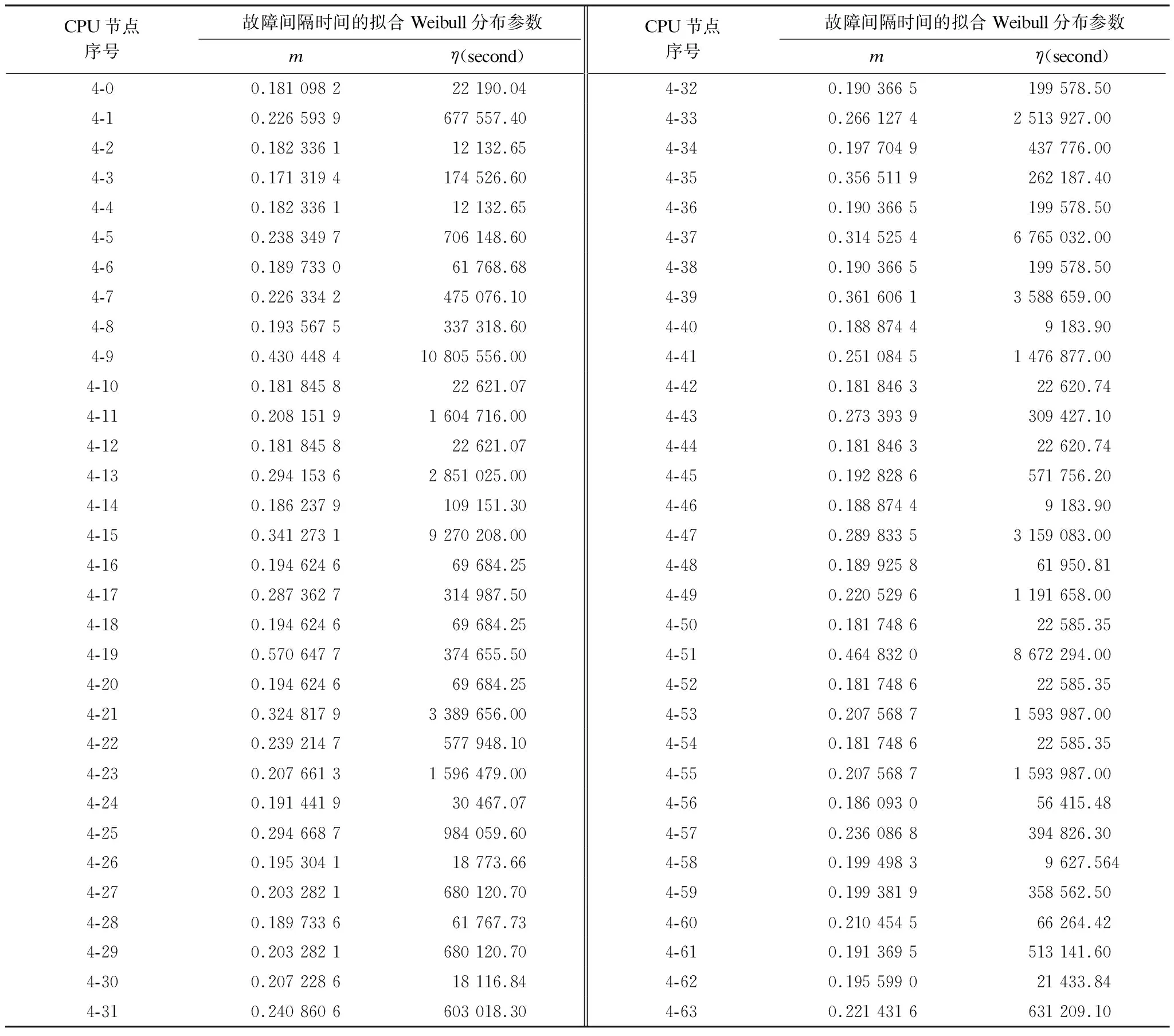
表5 CPU节点及其Weibull分布参数(m,η)
4.2 检查点间隔优化分析
使用检查点优化模型对2CPU、4CPU、8CPU、16CPU、32CPU和64CPU规模的应用进行检查点优化分析。结合最优化方法,得到典型的检查点保留开销下的最优检查点间隔时间,如表6所示。随着保留开销的增加,应用的最优保留间隔时间也随之增加。不同规模应用的平均中断时间(Mean Time To Interrupt,MTTI)如图10所示,可以看出,随着应用规模2的幂次递增,应用MTTI呈现指数级下降。一方面,是由于规模递增导致的可靠性下降;另一方面,由于CPU节点的可靠度差异,可靠度低的节点显著拉低了应用运行环境整体可靠性。
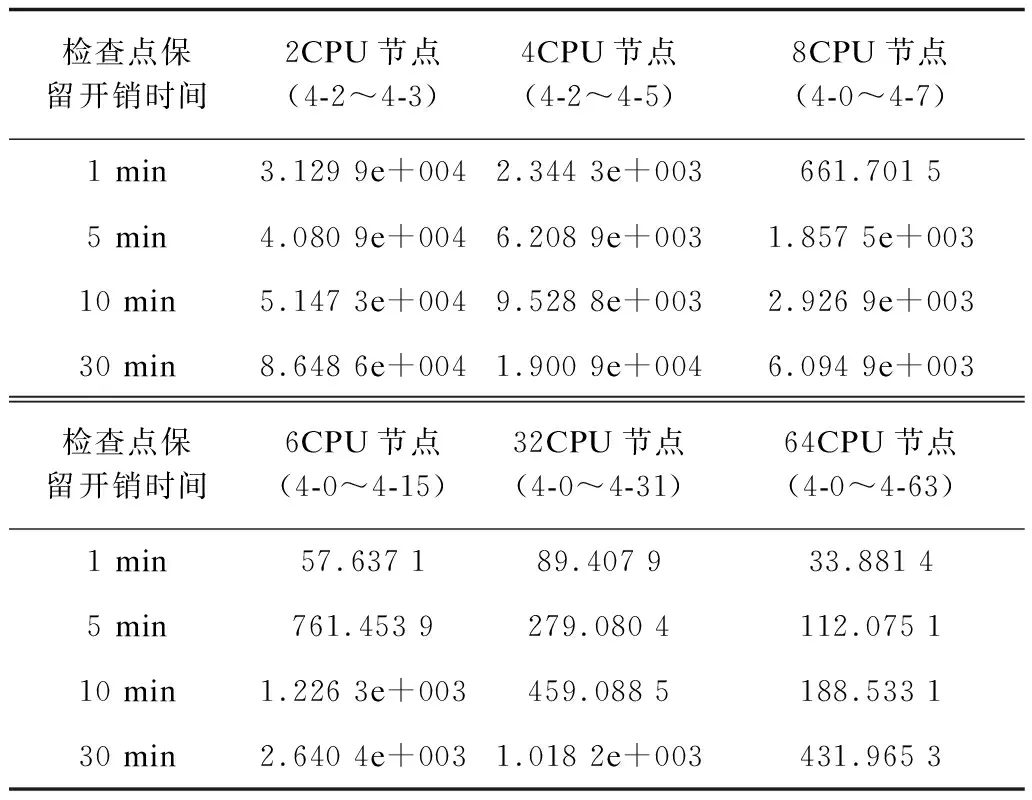
表6 最优检查点间隔时间Tc s

图10 不同规模的平均中断时间
最优检查点间隔曲线如图11所示,随着应用MTTI的下降,应用最优化保留间隔也随之减小,说明频繁的故障需要更加频繁地进行检查点保留,才能保护好已经完成的计算工作,降低故障损失。

图11 最优化检查点间隔
图12是不同应用规模在典型检查点保留开销下,常用检查点间隔时间与最优检查点间隔的容错开销对比。可以看出,在每种检查点保留开销(Ts=1 min、5 min、10 min、30 min)下,最优保留间隔时间下检查点容错开销都达到最小。例如,在4CPU应用规模下,在检查点保留开销为1 min时,最优检查点间隔造成的容错开销相比典型检查点保留间隔1 h、4 h、8 h和16 h下的容错开销,分别只有其90%、54%、37%和26%。可见,数据驱动的检查点优化方法,可以有效降低检查点容错开销,提高容错运行环境下的应用执行效率。
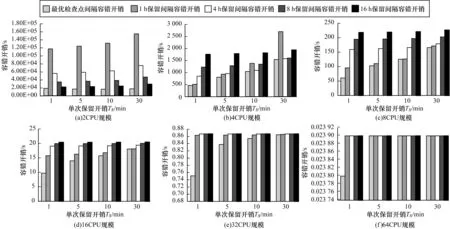
图12 各种应用规模下不同保留间隔的容错开销对比
此外,从2CPU~64CPU应用规模的检查点容错开销趋势中可以看出,随着规模上升,应用可靠性下降,当一次检查点保留开销接近甚至明显大于应用MTTI时,最优检查点间隔下的容错开销相比其他检查点间隔时间下的容错开销,已经没有明显的优势。此时,容错的开销已经接近应用的MTTI,说明检查点容错已经很难使用,因为应用运行时间基本都用于进行容错,真正执行时间非常少。如果没有有效地降低单次检查点时间开销的方法,则基于检查点的容错技术已经没有效果。如果在未来E级超级计算机中,应用运行环境平均无故障时间接近或小于一次保留的时间开销,那么检查点技术无法保证应用高效执行,只有提高可靠性、降低保留开销或者采用基于故障预测的前瞻容错技术才能保证应用的高效与容错运行。
5 结束语
本文基于太湖之光超级计算机的维护与监控基础架构,介绍了故障的采集、分类和预处理机制。针对超级计算机的主机系统故障,建立细粒度的故障分布模型描述主机系统复杂多样故障的特征,运用应用级失效分布模型评估应用运行的可靠性。利用超级计算机中典型的检查点容错技术,根据计算单元的动态故障特征和应用级失效模型,建立数据驱动的自适应容错模型。以太湖之光系统为例分析了检查点优化的方法和效果,验证了数据驱动自适应容错的有效性。

