基于MATLAB的六自由度焊接机器人的运动学仿真与轨迹规划
邢红辉,王保升,洪 磊,左健民,石朗春
(1.南京工程学院智能制造装备研究院,江苏 南京 211167)(2.江苏省智能制造装备工程实验室,江苏 南京 211167)(3.江苏省先进数控技术重点实验室,江苏 南京 211167)
随着中国制造2025的提出,科技水平的不断提升大大推动了我国的工业化。工业化水平的提高,生产技术的不断更新,使得产业向着自动化的方向不断发展。产业的自动化,需要工业机器人加入,从而促进了工业机器人的发展[1]。比如在自动化生产线上,用焊接机器人逐步取代人工焊接,这不但降低了劳动成本,而且还能提高焊接的效率与质量。在相对比较恶劣的环境下,机器人也能高效地完成焊接作业。针对现有的焊接机器人都具有的示教效率低、实验时间长等缺点,可以利用仿真软件模拟机器人的焊接过程,通过分析实验数据来评价焊接方案的可行性,从而减少实验时间,提高作业效率[2]。
1 机器人的运动学分析
1.1 机器人的结构与D-H坐标系
本文研究的ABB1410机器人是由腰关节回转(腰部)、肩关节俯仰(大臂)、肘关节俯仰(小臂)、腕关节回转(手腕)、腕关节俯仰(手腕)、腕关节侧摆(手腕)6个转动关节组成的。焊接实验中机器人在腕关节处安装焊枪,在肘关节处安装送丝机。根据标准的D-H[3]参数法,给ABB1410机器人建立必要的坐标系,并选取机器人腰关节坐标系作为基坐标系以简化运算。图1所示为机器人坐标系的简化线图。
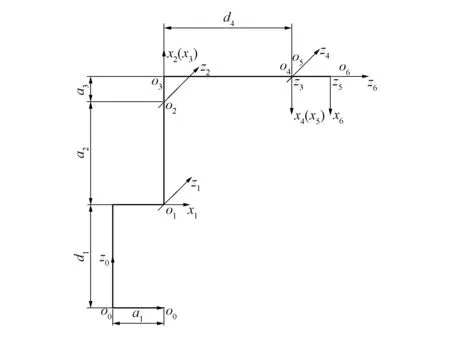
图1 ABB1410机器人D-H坐标系简化线图
根据机器人的整体结构和建立的简化坐标系,得出机器人连杆参数和关节变量,见表1。
1.2 正向运动学分析
在确定全部的连杆坐标系后,根据相邻两连杆i与(i-1)之间的相对关系[4](式(1)),将表1中关节转角θi、距离di、杆长ai、扭角αi代入计算,得到六自由度机器人的运动学方程(式(2))[5]。

表1 ABB1410机器人连杆D-H参数表
(1)
式中:i-1Ti为齐次变换矩阵,表示i连杆件坐标系相对于(i-1)连杆坐标系的方向与位置;Rz(θi)为xi-1轴和xi轴之间关于zi-1轴的角度;Dz(di)为沿zi-1轴,(i-1)坐标系原点到xi轴的距离;Dx(ai)为沿xi-1轴,zi-1坐标系原点到zi轴的距离;Rx(αi)为zi-1轴和zi轴之间关于xi轴的角度。
利用MATLAB编程计算机器人末端坐标系相对基座标系的变换矩阵,即六自由度机器人的运动学方程为:
(2)
式中:nx,ny,nz,ox,oy,oz,dx,dy,dz描述的是末端连杆相对于参考坐标系的姿态;px,py,pz表示的是机器人末端连杆相对于参考坐标系的位置;Ci=cosθi,Si=sinθi(i=1,2,3,4,5,6)。
2 正运动学仿真及结果分析
2.1 模型的建立
为了方便研究ABB1410焊接机器人在移动过程中末端位置的轨迹曲线,可以先建立机器人模型。根据表1中相关数据,利用MATLAB中的Robotics Toolbox工具箱,调用link函数,建立ABB1410焊接机器人的模型(如图2所示)。以下是相应的程序:

图2 ABB1410焊接机器人三维模型
L1=link([ 0 0.475 0.15 -pi/2 0 ]);
L2=link([ -pi /2 0 0.6 0 0 ]);
L3=link([ 0 0 0.12 -pi/2 0 ]);
L4=link([ pi 0.72 0 -pi/2 0 ]);
L5=link([ 0 0 0 pi/2 0 ]);
L6=link([ 0 0.085 0 0 0 ]);
robot=SerialLink({ L1 L2 L3 L4 L5 L6 });
robot.name = ‘ABB1410机器人’;
teach( r,[0-pi /2 0 pi 0 0]) ;
图2中右图所示是ABB1410机器人的初始状态,图左上方的数字表示的是机器人模型末端位置与姿态。通过驱动图中左下方的滑块,可以转动机器人的各个关节,其中移动滑块1,2,3可以改变机器人模型的末端位置,而滑块4,5,6是用来调整机器人的末端姿态。
2.2 正运动学结果验证
模型建立后,需要确定建立的模型是否正确,这样就要用到工具箱Robotics Toolbox中的fkine模块。至于验证内容,一方面是对机器人的正运动结果进行验证,另一方面是验证模型建立的准确度[6]。首先,在工作范围内任意给定机器人6个关节变量qb,然后调用fkine(r,qb)函数,就可以得到ABB1410机器人模型的末端位姿。假设关节向量qb=[pi/4 -pi/3 pi/6 pi/4 -pi/3 pi/6],经过MALTAB编程计算返回末端坐标系的变换矩阵T6;接着将关节向量qb代入式(2)中,同样也能得到末端坐标系相对于基础坐标系的变换矩阵。通过对比,可知计算得到的结果与上述结果是一致的,证明机器人模型建立成功,同时也证明正运动学方程是正确的。
3 MATLAB轨迹规划仿真验证
在MATLAB软件的Robotics Toolbox工具箱中用来规划机器人的关节空间轨迹的函数是jtraj。其原理是根据已知的初始与终止的关节角度,以及运动的持续时间,通过转动机器人的关节角度,使得末端连杆移动。而平滑变化的关节角被分成两路传送,一路传送到plot模块中,该模块能在一个单独的窗口中显示机器人运动过程的画面;一路传送到fkine模块中,用来求解机器人的正运动学方程[7]。可以先假设qa,qb为ABB1410机器人的起始位置与终止位置的关节向量,利用已建立的机器人模型,进行机器人末端位置的轨迹曲线仿真,得到如图3所示的ABB1410机器人末端空间轨迹曲线。轨迹规划程序如下:
t=[0:0.056:2];
qa=[0 -pi/2 0 pi 0 0];
qb=[pi/4 -pi/3 pi/6 pi/4 -pi/3 pi/6];
[q,qd,qdd]=jtraj(qa,qb,t);
T=robot.fkine(r,q);
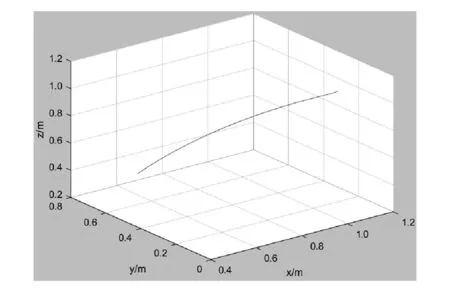
图3 ABB1410机器人末端空间轨迹曲线
通过MATLAB简单编程运行,得到的机器人移动轨迹是从初始位置到终止位置的一条圆弧,实现了机器人关节的空间轨迹规划。同时还可以利用fkine函数求解正运动学方程,计算可得机器人的任一关节的角位移、角速度和角加速度。图4所示为ABB1410机器人末端的位置在3个坐标轴上的投影坐标随时间变化的曲线,从曲线的变化可以看出机器人末端运动平稳且连续。图5所示为ABB1410机器人模型中关节2的角位移、角速度、角加速度随时间变化的曲线,从图中可以看出,关节2的速度、角速度随着时间变化连续而且平缓。经仿真可知,ABB1410机器人在进行实际焊接作业时,末端焊枪的移动是平缓的,机器人的6个关节以及运动部件的运动也是相对稳定的。

图4 机械人末端执行器坐标变化曲线
4 机器人的轨迹规划实验
本实验装置包括ABBR1410机器人、焊枪、焊接件、实验平台等。
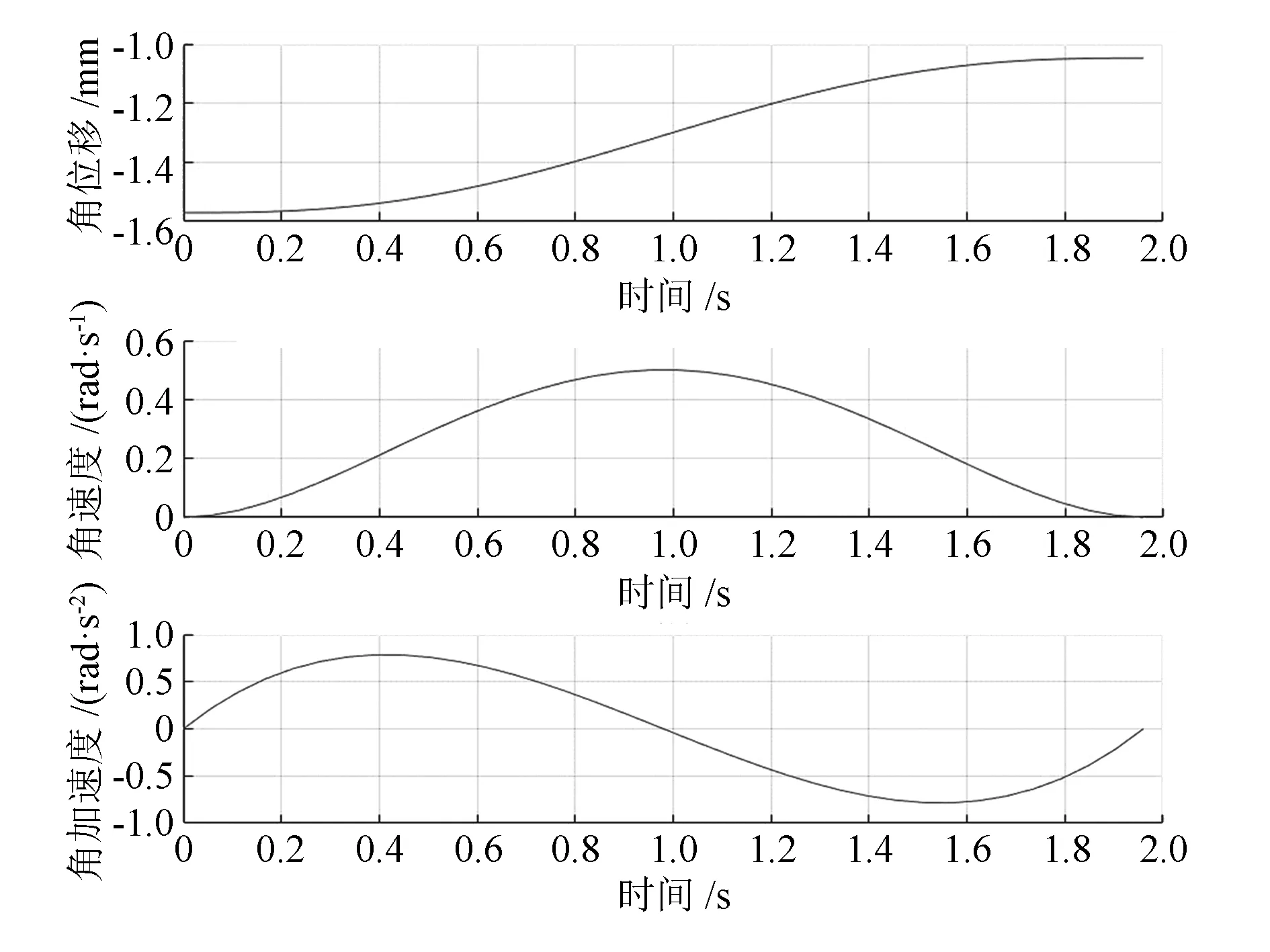
图5 关节2角位移、角速度、角加速度随时间变化曲线
实验步骤:1)确定实际作业时ABB1410机器人与焊接件之间的相对位置,让机器人对焊接件位置进行采点,通过得到的点的位置拟合出焊接件相对于机器人基坐标系的位置;2)根据得到的ABB1410机器人与焊接件之间的相对位置关系,在SolidWorks软件中对ABB1410机器人与焊接件进行三维建模并确定两者之间的位置;3)设定机器人腰关节的运动坐标系为基坐标系,并在三维模型中提取焊缝上特征点的三维坐标;4)如图6所示,利用ABB1410机器人对实际焊接的焊缝进行采点,最后分别从建模与实物上取10组点的三维坐标,见表2。

图6 ABB1410机器人焊接实物图

表2 建模采点值与实物采点值比较
比较两组点的起点与终点的三维坐标,根据式(4)分别计算点的x,y,z坐标的误差。
(4)
式中:Δ误差为模型点与实物点的坐标误差;psim为模型中轨迹点的坐标;pact为实物中轨迹点的坐标。
通过计算可知,起点与终点的位置存在误差(见表3),但是误差较小,误差的来源可能是实际驱动机器人采点位置时出现的不准确。
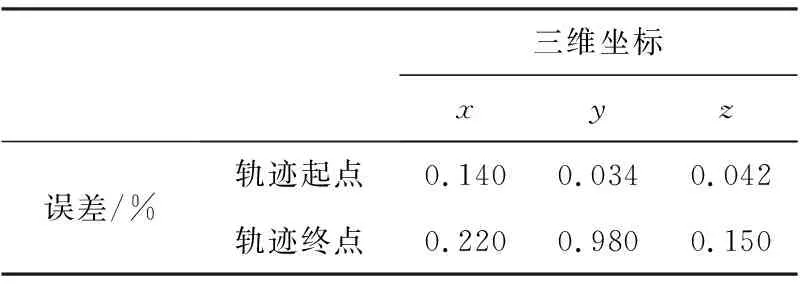
表3 仿真与实物中轨迹起点与终点的误差
只计算起始点的误差并不能得到2条轨迹的误差,也不足以证明仿真轨迹与实物轨迹具有良好的一致性。但是由于在轨迹上取点位置的不统一,不能直接比较除起点与终点以外的8组点。这里可以使用MATLAB中的拟合工具箱,利用得到的2组10个点拟合出轨迹曲线进行比较。从图6实物图中可以看出,焊接轨迹上的点基本属于同一水平面;从表2可知,无论是建模采点还是实物采点,在z轴方向的变化都较小且保持在623左右也说明了这一点。因此先将z轴坐标的变化忽略不计,只研究点的x与y坐标。利用MATLAB中拟合工具箱得到两组点的x与y坐标的拟合公式:
(5)
(6)
式中:xsim和ysim为从模型中提取的坐标数值;xact和yact为从实物中提取的坐标数值。
令横坐标xsim=xact,计算2个拟合公式中的纵坐标,通过对比纵坐标的值,来确定由2条轨迹上的点分别拟合而成的方程的误差。任意取xsim=xact=1 015mm代入式(5)和式(6),得到:
ysim=157.23mm
yact=159.76mm
(7)
通过式(7)计算结果可知2个拟合公式中取同一横坐标时,纵坐标相对误差较小。2个拟合公式是根据2条轨迹上取得的点得到的,这结果表明2条轨迹曲线上横坐标相同的点,它们的纵坐标的相对误差比较小。
根据所得到的点的x与y坐标的相互关系,利用MATLAB中的工具箱绘制出拟合的曲线,如图7所示。图7(a)是从ABB1410机器人与焊接件的模型上提取的三维坐标点拟合的轨迹曲线;图7(b)是实际中驱动ABB1410机器人从焊接件上提取的焊缝点,并由这些点拟合而成的轨迹曲线。从2条轨迹曲线的对比来看,轨迹曲线总体相似,但是2条轨迹曲线上横坐标相同的点,它们的纵坐标还是存在相对误差。根据2条轨迹曲线的拟合公式(5)与(6),计算得到的结果(式(7) )表明两者之间误差比较小,从而证明三维建模上的轨迹曲线与实际中的曲线具有良好的一致性。与此同时,实验还证明了在MATLAB中研究机器人的轨迹规划以及仿真的可行性。
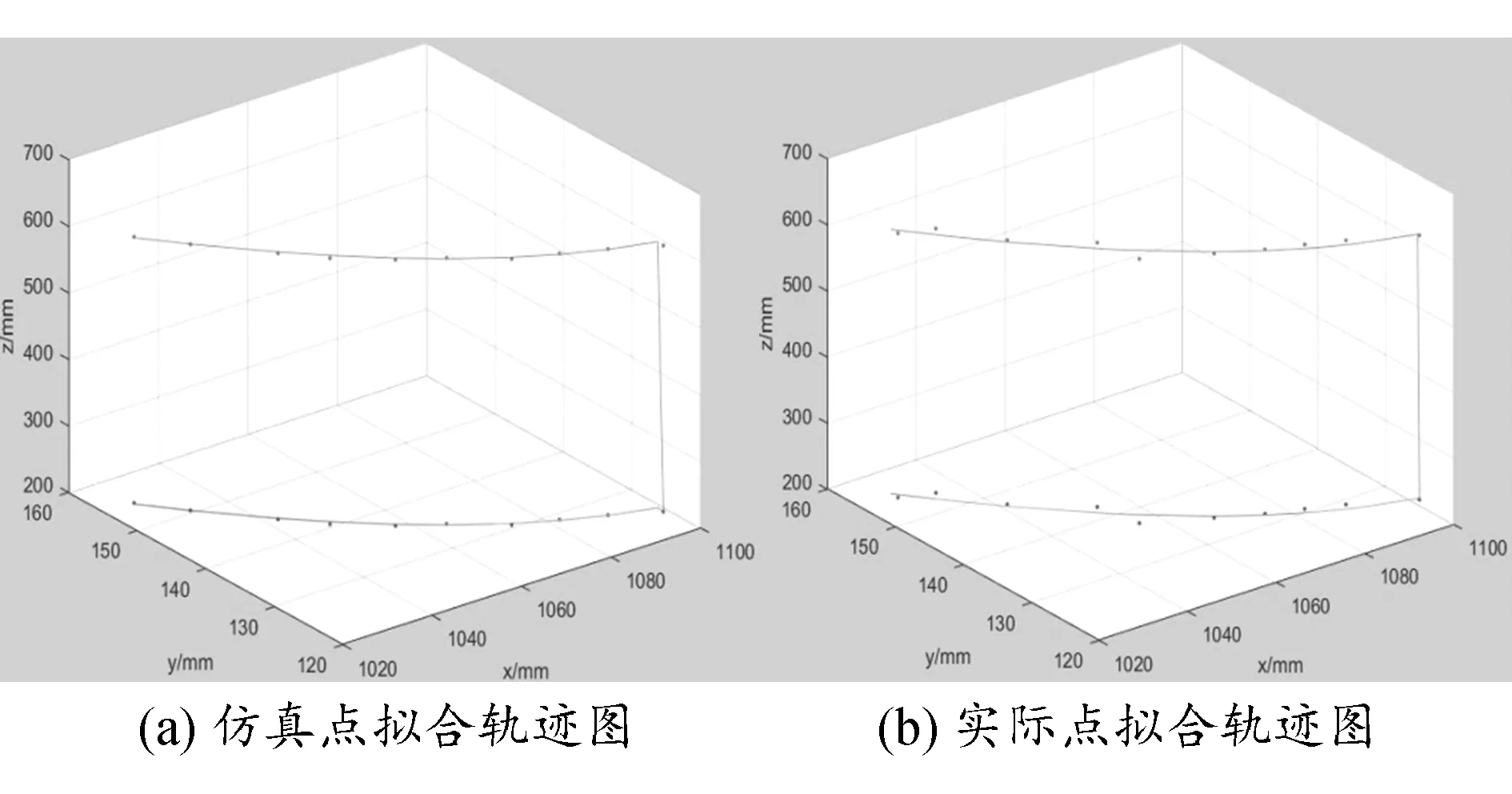
图7 轨迹拟合曲线图
5 结束语
本文主要研究仿真软件中模拟焊接机器人的轨迹规划,倾向于理论方面的研究。文中得到的机器人末端的关节空间运动的轨迹曲线,以及末端位
置在三坐标轴上的投影点的时间变化曲线和关节2的角位移、角速度、角加速度变化曲线,表明机器人在空间运动时运动连续且平稳,符合焊接工业机器人实际作业时各部件运动平缓的要求,为后续的实验提供了理论分析依据。
本文通过对比由两种方式得到的同一轨迹曲线,可知利用SolidWorks建立的三维模型中仿真焊缝轨迹与实际焊缝轨迹具有良好一致性,证明利用仿真软件进行轨迹规划具有较高的精度,可为后续的离线编程提供三维模型与轨迹规划仿真的理论基础,同时也验证了在MATLAB中研究机器人的轨迹规划以及仿真的可行性。

