多次冲击下泡沫铝动态压缩力学性能试验与本构模型研究

高华， 熊超， 殷军辉

(陆军工程大学石家庄校区 火炮工程系， 河北 石家庄 050003)

0 引言

泡沫铝材料作为一种轻质高强材料，具有良好的抗爆缓冲、吸能等性能[1-4]，在军事防护、航空航天等领域应用广泛，尤其对于装甲防护车辆，抗多次打击能力是评价其防护性能的重要指标。因此，研究泡沫铝材料多次冲击下的动态力学性能对科学研究及工程应用具有重要价值。

国内外研究人员在材料参数及应变率对泡沫铝动态力学行为的影响[5-7]、高温动态加载时材料的变形过程[8]以及泡沫金属材料的动态本构模型建立[9-10]等方面做了大量研究工作。Myers等[11]对不同基体材料(铝、镁)以及经过不同热处理的泡沫金属材料高应变率下的力学行为进行了分析，结果表明基体材料和热处理方式对材料的压缩性能有很大影响，不同应变率下材料呈现不同的冲剪失效模式。Wang等[12]借助高速摄影技术对泡沫铝在高温下的动态性能进行了分析，发现随着温度的升高，材料应变率效应越明显，相对于室温材料发生剪切断裂破坏，高温下以塑性弯曲失效模式为主。张勇等[13]利用霍普金森压杆冲击试验，分析了包含温度、相对密度及应变率等因素的聚氨酯泡沫铝材料的动态力学性能，建立了适用于相对密度和应变率在一定变化范围的动态本构模型。

上述研究均是针对泡沫金属材料在单次冲击下的动态力学性能，而多次冲击加载在材料内部造成的损伤累积对材料动态力学性能产生的影响极为复杂[14]，目前尚未见系统研究。本文利用分离式霍普金森压杆(SHPB)装置进行泡沫铝中低应变率下多次冲击的动态力学性能试验研究，分析了不同初始冲击能量及冲击加载次数下，弹性极限应力、应变、理想吸能效率的变化规律，在此基础上引入损伤累积变量，建立了泡沫铝多次冲击下损伤累积本构模型。

1 试样制备及试验装置

1.1 试样制备

试验用材料为闭孔泡沫铝，密度为0.5 g/cm3，平均孔径为4 mm. 将泡沫铝作为连续介质，要获得其有效的材料力学特性，试样尺寸要大于泡沫孔径的10倍[15]，同时减小惯性效应[16]带来的误差，为此选取直径为40 mm、厚度为20 mm的试样进行试验。泡沫铝试样采用线切割技术加工，以减少加工过程中试样胞孔的损伤。

1.2 试验装置

SHPB试验装置主要由撞击杆、入射杆、透射杆和吸能杆组成，如图1所示。

由于泡沫铝试样为低阻抗多孔材料，透射杆波阻抗与试样相差较大，使得透射信号微弱，与外界干扰信号处于同一量级，将严重影响测试结果，因此本文设计如下改进方案：试验用SHPB采用波阻抗较小的铝合金材料，入射杆上采用电阻应变片，透射杆上采用高灵敏度系数半导体应变片(试验所用半导体应变片灵敏度系数为110，是电阻应变片的55倍)记录应变信号。为了增加应力波上升沿时间以满足试样内部应力平衡，试验过程中采用8 mm×8 mm×3 mm硅橡胶作为波形整形器，动态压缩试验中，在泡沫铝试样两端面涂抹凡士林，以减少变形时与压杆端面间的摩擦。试验压杆直径为50 mm，撞击杆、入射杆和透射杆长度分别为300 mm、1 500 mm、1 500 mm，利用SHPB装置对泡沫铝进行多次加载，通过控制推动撞击杆的气压大小改变打击速度，通过增加压力传递法兰和反应质量块[17]确保每次加载为单次加载。

图2给出了改进前后试验的入射波、反射波和透射波信号。由图2可见，改进后透射波信号得到了明显改善，应力波上升沿时间增加。

根据应力均匀假定，采用经典两波法，通过(1)式、(2)式和(3)式计算得到试样在不同应变率下的应力- 应变曲线。

(1)

(2)

(3)

式中：A、c和E分别为压杆横截面积、波速及弹性模量；As、Ls分别为试样横截面积及厚度；εi(t)、εt(t)分别为入射信号和透射信号测得的应变，t为应力脉冲持续时间。

2 动态力学试验及性能分析

下面利用SHPB装置对泡沫铝进行多次加载，在分析不同冲击次数下材料破坏形貌变化的基础上，研究材料透波率、应力- 应变曲线、吸能效率随冲击损伤累积的变化规律。

2.1 多次加载破坏形貌分析

为分析泡沫铝试样在不同冲击次数下的破坏过程，选取5个试样分别进行1～5次冲击加载，撞击杆速度均为10 m/s. 对冲击后试样沿加载方向进行线切割，其剖面如图3所示。

由图3可以看出：冲击后试样1～5的直径分别为41.40 mm、42.11 mm、43.25 mm、44.67 mm、45.52 mm，厚度分别为16.86 mm、13.65 mm、11.19 mm、9.24 mm、7.36 mm；试样1仅进行了1次加载且冲击速度较低，沿加载方向的胞孔结构并未发生明显变形；随着冲击次数的增加，胞孔结构发生失稳变形，出现了崩塌压实现象。

2.2 波动性能分析

为分析初始冲击损伤程度不同对泡沫铝多次冲击的力学性能影响，选取3个试样(编号A、B、C)进行如表1所示的加载，3个试样所受撞击杆初始速度不同，其中A、B进行5次加载，试样C由于初始冲击速度较高，经4次加载后产生径向断裂，不再适合冲击加载。在试验过程中，发现当撞击速度较大时初始撞击下即发生很大程度的变形，不能进行多次冲击；当撞击速度较小时，胞孔变形程度很小，损伤累积效应不明显。为分析损伤累积对多次冲击下泡沫铝力学性能的影响，最终确定撞击速度在14.0～22.0 m/s较为合适。本文以14.0 m/s、17.9 m/s、22.0 m/s为初始冲击速度进行分析。由于试验过程中需要对试样A、B、C进行多次加载，不能进行剖面切割，在试验完成后选取相同规格试样D、E、F，分别进行与试样A、B、C相同条件下的初次加载(即D加载速度为14.0 m/s，E加载速度为17.9 m/s，F加载速度为22.0 m/s)，并对冲击后试样沿加载方向进行线切割，得到其剖面如图4所示。由图4可知，随着初始冲击速度的增加，其胞孔崩塌变形程度增加，导致其初始损伤累积效应不同。图5为试样A、B、C在多次冲击下测得的入射信号、反射信号和透射信号应力- 时间曲线。

表1 试样加载状况

由图5可以看出不同冲击次数下试样的透波性能：1)从入射波形来看，除试样B、C由于首次冲击速度较大、第1次入射波幅值较高外，其余信号幅值基本相等；2)从反射波形来看，反射波的幅值略小于入射波；3)从透射波形来看，随着冲击次数的增加，透射波幅值逐渐增大，但相对于入射信号和反射信号而言幅值较低。

下面根据图5所示曲线计算透波率(透射波峰值与入射波峰值的比值)，分析泡沫铝不同冲击次数的透波效果(见图6)。由图6可见，对于初次加载，试样透波率明显较低，内部胞孔结构完好，对于应力波的传播阻抗作用较强，随着冲击次数的增加，损伤累积不断增加，材料被压实，阻波性能减弱，透波率逐渐增加。

2.3 动态应力- 应变分析

图7为泡沫铝试样A、B、C在不同冲击次数下的应力- 应变曲线。由图7可见，该曲线可以分为2个阶段：初始阶段，泡沫铝发生弹性变形，应力随应变线性增加；当到达胞孔破坏强度时进入屈服阶段，应力不再增加。由于撞击杆冲击能量较低，并未出现高应变率加载中的致密区特性(应力随着应变的增长而迅速增加)。

对比不同加载次数下的应力- 应变曲线发现，初始加载情况下屈服阶段较为平缓，随着加载次数的增加，应力幅值出现波动，这是因为初始加载下胞孔结构到达屈服破坏的临界状态，随着损伤累积，胞孔结构孔壁破裂或破碎程度增大并出现卸载，使得应力出现较大程度的波动。

图8为泡沫铝试样A、B、C的弹性极限应变以及对应应力随冲击次数的变化规律。由图8可见：1)对于试样A，撞击杆首次冲击速度与多次冲击速度基本相同，试样的弹性极限应变随冲击次数的增加呈上升趋势；2)对于试样B、C，撞击杆首次冲击速度高于多次冲击速度，初始冲击下弹性极限应变明显高于多次冲击下弹性极限应变值，在多次冲击中，随冲击次数增加弹性极限应变也呈增长趋势；3)3个试样在相同冲击次数下，随着试样初始冲击能量的升高，胞孔结构压实程度越强，到达弹性极限应力对应的应变越小；4)随着冲击次数增加，弹性极限应力近似呈指数增长，表现出明显的增强效应，而且对于初始加载强度越高的试样，相同冲击次数下的弹性极限应力也越高。

上述变化是由于泡沫铝试样受到冲击载荷作用后胞孔结构产生压弯失稳，内部结构松散破碎，再次受到冲击作用时在弹性极限应力处更容易产生较大应变，但随着胞孔结构压实，泡沫材料发生变形困难，弹性极限应力出现增强效应，而弹性极限应变增强效应被削弱。

2.4 吸能分析

为表征不同加载次数下泡沫铝材料的吸能特性，下面对其理想吸能效率进行分析。

理想吸能效率η[18]即泡沫铝材料实际吸收能量与理想塑形- 刚性泡沫铝在相同应变下的吸能量之比，作为衡量泡沫金属材料吸能强弱的指标，其计算公式为

(4)

式中：σ、ε分别对应应力- 应变曲线的取值；σmax为泡沫铝变形过程中的峰值应力。

图9为泡沫铝试样A、B、C在不同冲击加载次数下的理想吸能效率曲线图。由图9可见，在多次冲击加载下，随着应变的增加，理想吸能效率逐渐增加，最终趋于平缓。在低速加载中，初次冲击加载的理想吸能效率最低，第2次加载的理想吸能效率最高，之后随着冲击加载次数的增加，理想吸能效率逐渐降低。由此可知，泡沫铝材料的最佳理想吸能效率并非在最初无损伤状态下，胞孔结构处于屈服或向压实状态转化过程中产生损伤累积效应，更有利于提升泡沫铝的吸能效率。

3 损伤累积本构模型

3.1 本构模型建立

泡沫铝多次冲击下的损伤累积效应使其动态力学性能十分复杂，下面结合实测应力- 应变曲线，基于Sherwood-Frost方程并引入损伤累积变量构建本构模型。泡沫金属材料通用的Sherwood-Frost经验型本构关系框架[19]为

(5)

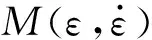
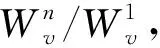
(6)

(7)

(8)

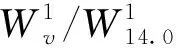
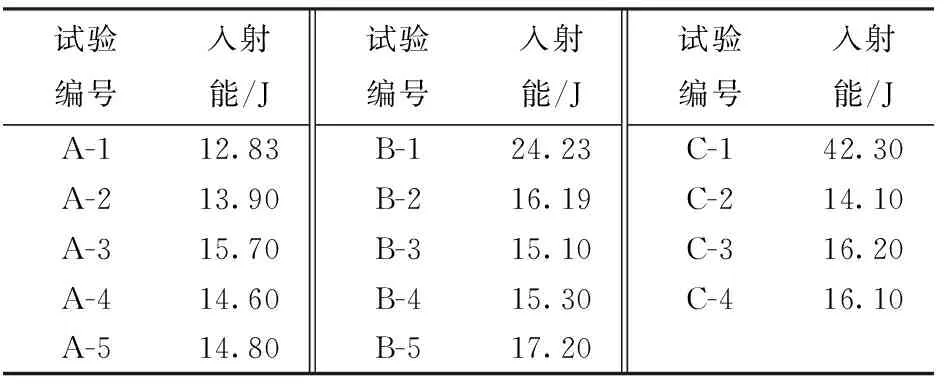
表2 不同冲击加载下能量分布

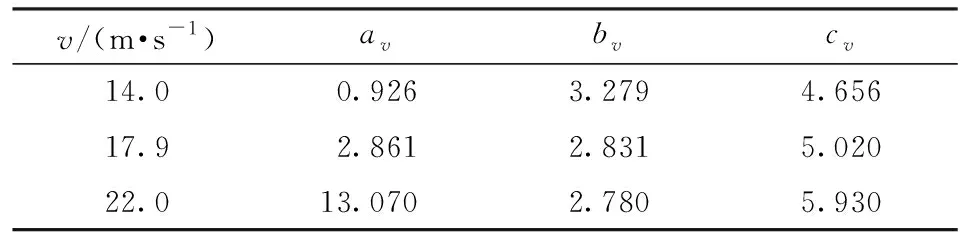
表3 弹性极限应力拟合参数

(9)

(10)

(11)

Sherwood和Frost[15]通过幂级数表示形状函数f(ε)，其表达式为

(12)

式中：q为幂级数展开项数；Ep为形状函数拟合参数；σ0为对应的弹性极限应力。(12)式描述了泡沫铝在给定参考密度、参考初始冲击能量以及参考损伤累积下的应力- 应变曲线形状，选取前述试验编号C-2得到应力- 应变曲线作为参考曲线，以q=10的级数形式对形状函数进行拟合，得到形状函数拟合参数如表4所示。

表4 形状函数拟合参数

由此可得泡沫铝多次冲击下的损伤累积本构模型如(13)式所示：

(13)

为验证本构模型，对试样进行了初始入射能为35.87 J且随后3次入射能分别为14.1 J、15.7 J、15.3 J的多次冲击加载试验，将第2次、第3次和第4次冲击加载得到的应力- 应变曲线与本构模型得到的应力- 应变曲线对比，结果如图10所示。

图10所示结果表明，通过损伤累积本构模型预测的应力- 应变曲线与试验测得的应力- 应变曲线吻合较好。相对于第2次和第3次冲击预测应力- 应变曲线，第4次冲击预测应力- 应变曲线与试验结果的离散性有所增加。

3.2 本构模型影响因素分析

图11分别给出了不同冲击次数本构模型与试验所得的弹性极限应力。由图11可见，对于3.1节试验中的第2次、第3次和第4次冲击，本构模型得到的弹性极限应力分别为6.00 MPa、7.70 MPa、10.37 MPa，试验测得的弹性极限应力分别为6.11 MPa、8.00 MPa、10.52 MPa，二者对应的误差分别为1.80%、3.75%、1.42%. 由此可知，由本构模型得到的弹性极限应力与试验结果吻合良好，不同冲击次数下的误差相差不大。

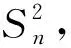
(14)

式中：σsj、σej分别为第j个点数据采集对应的本构模型预测应力和试验测得应力；m为试验采集点数。

以上研究表明，第2次和第3次冲击由于损伤状态与前述试验C-2相近而取得了较好的拟合效果，第4次冲击则由于损伤累积效应导致一定的拟合误差，泡沫铝在多次冲击下的损伤累积使其本构模型更加复杂。因此，根据泡沫铝冲击加载试验曲线特征选取最佳形状函数，是基于上述损伤累积本构模型进行多次冲击下动态力学分析的重要前提，形状函数参考曲线累积损伤能量与多次冲击对应累积损伤能量差值越小，得到的本构模型预测效果越好。

4 结论

本文对泡沫铝在多次冲击下的动态力学性能进行了研究，并在试验的基础上构建了损伤累积本构模型。本文的贡献及主要结论如下：

1) 利用SHPB装置对泡沫铝进行中低应变率下的多次加载时，随着冲击次数的增加，胞孔结构逐步崩溃压实，对应力波的衰减作用减弱。

2) 随着冲击次数的增加，弹性极限应变呈上升趋势，弹性极限应力呈近似指数形式增长，表现出明显的增强效应；在相同冲击次数下，初始冲击能量越高，对应的弹性极限应力越高、弹性极限应变越小。

3) 本构模型形状函数参考曲线对应的累积损伤能量与试验累积损伤能量越接近，预测曲线与实际应力- 应变曲线吻合越好。

综合考虑泡沫铝密度和试验温度等影响因素，建立更加完善的泡沫铝损伤累积本构模型，将是下一步的研究重点。