推进电机的模态分析与实验研究

刘 磊，赵国平，魏 娟，郑 林，田冠枝

(北京精密机电控制设备研究所，北京100076)

0 引言

参数结果是可信的。

近年来，推进电机越来越广泛地应用于舰船领域。作为一种旋转设备，推进电机在运行过程中将不可避免地产生振动，这不仅降低了舰船的隐身性能，也会影响舰船的效率、结构强度等综合性能。由振动引发的噪声还会影响舰船的舒适性，危害人体健康［1］。因而，振动水平成为推进电机的核心指标之一，其振动特性研究具有重要意义和实用价值。

推进电机中存在多种频率的电磁力，这些激励是引发振动的根源之一。推进电机电磁力的分布规律［2］已初步掌握。然而，电机的振动是电磁场和结构场相互作用的结果，当激励频率与电机结构的模态固有频率相近时，电机的振动尤为剧烈。因此，对推进电机的结构特性进行研究，准确识别模态参数是降低推进电机振动和噪声的前提。现有文献中，电机模态的分析大多集中在定子或转子某一单一结构［3－4］，忽略了电机整机的模态特性。本文针对一台推进电机进行模态分析，考虑了定子和转子的耦合，建立了电机结构完整的有限元模型，通过仿真方法求解了电机的模态参数;在电机工作状态下，基于运行模态分析的实验方法识别了电机的固有频率，验证了有限元仿真方法的准确性，同时也证明模态

1 模态分析的数学模型

根据动力学理论，系统的振动遵循如下的微分方程:

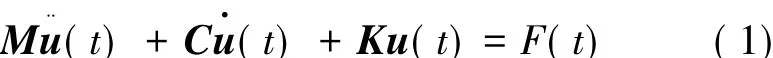
式中:M，C，K分别为系统的质量矩阵、阻尼矩阵、刚度矩阵;u¨(t)，u·(t)，u(t)分别为系统各质点的加速度向量、速度向量、位移向量;F(t)为系统所受的外力。

模态分析基于系统的无阻尼自由振动，即:

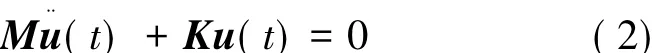
设想系统产生同频率、同相位但各质点不同振幅的振动:

将式(3)代入式(2)，得这一运动需满足的条件是存在非零向量φ，使:

满足式(4)的特征根ωr即为系统模态的固有频率，非零解向量φr即为对应频率下的振型。

2 推进电机的有限元模态分析

推进电机由定子、转子、轴承座、机壳等部件组成。为提高运算效率，建模时进行了简化，忽略了小孔、倒角、圆角等对结构模态参数影响较小的特征。

材料特性参数如表1所示。为同时考虑绕组的质量和刚度对电机模态的影响，按照槽满率折算定子绕组的密度。

表1 材料参数

推进电机通过4个螺栓孔固定在工装上，对4个螺栓孔施加固定约束以限制其位移;电机的转子与定子在结构上通过轴承发生耦合，使用轴承连接(图1中轴承1、轴承2、轴承3所示)模拟轴承的支承。

将轴承等效为具有一定刚度的弹簧，刚度大小按下式计算［5］:

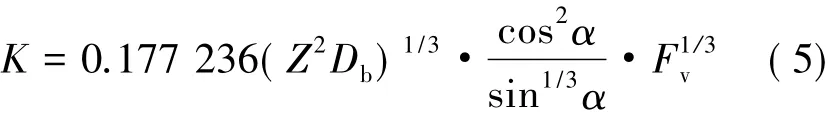
式中:Z为轴承滚动体个数;Db为滚动体直径(单位为μm);α为接触角(单位为°);Fv为轴承的轴向预紧力。计算得到的3个轴承的等效刚度分别:K1=K2=1．31× 108N/m ，K3=1．28 × 108N/m 。

最终建立的有限元等效模型如图1所示。对前5阶模态进行求解，模态固有频率的结果列于表2。

图1 推进电机三维模型

表2 有限元仿真结果

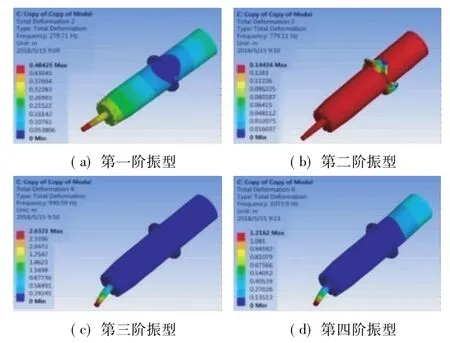
图2 前五阶模态振型

前几阶模态振型如图2所示，电机的第一、二阶振型分别是以法兰盘固定位置为中心的整机摆动和轴向往复平移，第三、四阶振型以转子轴和机壳的局部弯曲变形为主，第五阶振型则表现为机壳和定子的径向伸缩。

3 运行模态分析

传统的实验模态分析(EMA)方法通过锤击测试对象而施加外激励，并同时拾取激励信号和响应信号，估计测试对象的频率响应函数，进而获得模态参数［6］。与试验模态分析方法不同，运行模态分析(OMA)仅需测试对象在运行状态下的输出响应，就可以识别模态参数。由于不需要激励系统，运行模态分析实验成本较低，而且避免了外激励对测试对象可能造成的损伤;实际运行状态下的边界条件和激励亦有利于模态参数识别准确性的提高［7］。综合以上原因，运行模态分析实验方法得到了越来越多的应用。

3．1 自互谱法

运行模态分析有多种不同的模态参数识别方法，诸如峰值拾取法、频域分解法、时域子空间法等［8］。自互谱法是峰值拾取法的改进，可排除周期性激励的干扰，选择该方法进行模态频率的识别。

系统的响应u(t)等于其激励f(t)和系统的脉冲响应h(t)的卷积，即:

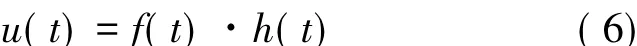
根据卷积定理，式(6)在频域中可表示:

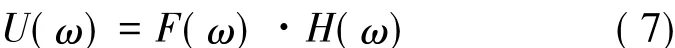
式中:H(ω)为系统的频率响应函数，它包含了系统的质量、刚度、阻尼等信息，在频域上反映了系统的动态特性，可通过实测频响函数求取模态参数。

对式(7)两端乘以U(ω)的复共轭并取期望值:

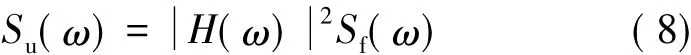
式中:Su(ω)，Sf(ω)分别为系统响应和激励的自功率谱。

当激励信号为白噪声时，其能量在频域上近似呈现为均匀分布的状态，即:

将式(9)代入式(8)，可得:

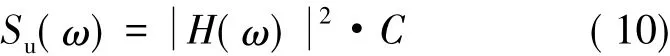
式(10)反映了激励与响应的功率谱和频响函数间的关系。显然，由于激励功率谱按频率的分布为常数，系统的频响函数与响应的自功率谱具有相同的频谱特征，因此，可以由系统的响应求取固有频率。

以上推导的前提是激励信号为均值白噪声。然而，作为一种旋转机械，电机运行时必然会伴随周期性激励信号，如果周期信号的能量较强，就会引起相应频率较大的响应，在模态参数识别时会造成误判，由此引入虚假模态［9］。为排除周期信号的干扰，首先可以通过滤波方法滤除已知频率的周期性干扰信号;其次，当结构某阶振动发生时，测点之间振动的相位差要么为0(同相)，要么为180°(反相);最后，若峰值频率处各响应信号间相干性较高，也可排除虚假模态的可能［10］。因此，按照以下步骤识别推进电机的模态固有频率:

(1)根据测点响应结果，绘制两响应信号的平均自谱曲线以及测点间的互谱相位曲线和相干函数曲线，为使结果更加准确，需多次测量取平均值;

(2)读取自谱曲线峰值对应的频率，初步筛选固有频率;

(3)对初筛频率进行判定，对应频率处，若互谱相位在 0或 180°附近(±30°)，相干函数值大于0.95，即可排除虚假模态的可能，确定为固有频率。

3．2 推进电机的运行模态实验

实验系统及现场如图3、图4所示。推进电机通过工装固定，在变频器控制下运行。在电机轴向布置两个加速度传感器，拾取振动信号。节点处振动响应信号极为微弱，应避免将传感器粘贴在节点上，节点的位置由有限元仿真得到的振型确定。振动信号经数据采集仪采集，传入计算机进行分析。实验进行3次测量取平均值。

图3 实验系统框图

图4 实验现场

振动响应信号的自谱曲线如图5所示。在自谱曲线中，134 Hz处存在一个较高的峰值，根据电磁学理论，此频率为2倍频电磁力的频率，属于周期性激励信号，对于模态固有频率的识别将造成较大干扰，在分析前应当予以滤除。使用MATLAB设计一个八阶Butterworth带阻滤波器(滤波器响应性能如图6所示)对信号进行滤波，滤除干扰后的自谱幅值曲线如图7所示，峰值处对应的频率分别为295.3 Hz，769．8 Hz，829．3 Hz，879．3 Hz，961．7 Hz，1083.2 Hz，1270．4 Hz，1659．5 Hz;之后，继续观察互谱相位(图8)及相干函数曲线(图9)，各频率对应的数值如表 3 所示。其中，295．3 Hz，769．8 Hz，961．7 Hz，1083．2 Hz，1659．5 Hz 均满足相干函数值在 0．95以上、互谱近似同相的条件，确定为模态频率;其他频率不同时满足判定条件，为虚假模态频率。

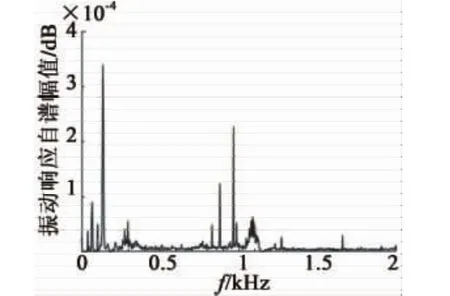
图5 振动响应信号自功率谱

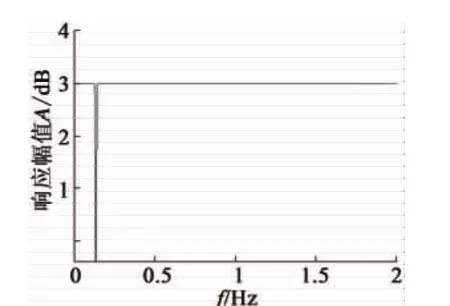
图6 八阶Butterworth带阻滤波器响应特性

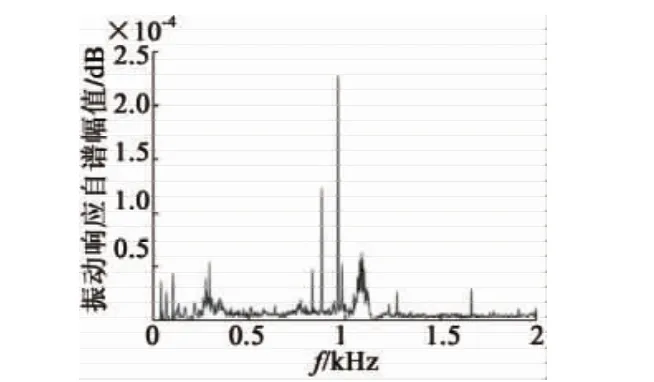
图7 滤波后的振动响应信号自功率谱

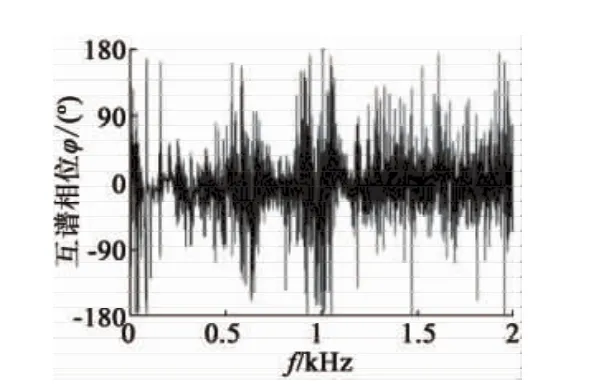
图8 振动响应信号间互谱相位

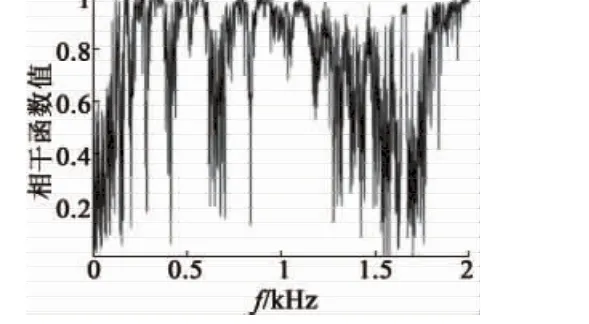
图9 振动响应信号间相干函数

表3 峰值频率对应的频谱信息

实验结果与有限元仿真结果对比如表4所示，两者结果相近，说明获得的模态参数结果是可信的。但两者结果仍有所差异，这主要是因为电机系统的机械结构十分复杂，在建立仿真模型时，必须予以简化;另外，仿真分析过程中边界条件的模拟难以与实际情况完全一致。

表4 实验与仿真结果对比分析

4 结语

以一台无人水下航行器推进电机为对象，对其开展仿真和实验研究，得到了以下结论。

(1)仿真模型可以求得系统的振动特性，为推进电机设计阶段结构的优化调整提供了基础。

(2)通过运行模态分析方法，在电机工作状态下实现模态参数的识别，为其他同类电机的模态实验研究以及水下环境中真实边界条件下推进电机的振动特性实验测量提供了参考，具有一定的工程实用价值。

(3)获得的模态参数为推进电机的减振降噪提供了依据。电机前三阶模态频率分别为295．3 Hz，769．8 Hz，961．7 Hz，容易与外激励耦合发生共振，因此，可以优化电机结构或修改电机极槽配合，使固有频率远离激励频率;电机前两阶振型为整体的振动，后三阶为局部的振动，其中，整体振动均以法兰盘为中心，因此，可以考虑加厚法兰结构以抑制推进电机的振动。