基于分位数回归的娘子关泉降水及径流变化分析

王永珂，范永辉

（天津师范大学数学科学学院，天津300387）

娘子关泉域地处山西省阳泉市，是当地主要的供水水源，对其降水及径流变化规律的研究具有重要的理论与实践意义.现已有许多文献对不同水域降水、径流之间的响应关系进行了研究，主要采用趋势分析[1-2]或水文模型[3-4]等方法.分位数回归模型最早由Koenker等提出[5]，之后随着对该模型的研究和推广，其广泛应用于经济、医学、教育、生物学等领域.相比其他方法，分位数回归能够更充分反映自变量对不同部分因变量的分布产生的不同影响，即它能在很大程度上提供数据的全部信息.分位数回归的估计量不易受到异常值的影响，具有很强的稳健性，且分位数回归不需要对模型中的随机干扰项做任何分布的假定，使模型具有很强的适应性.近些年，该方法被逐步应用于水文气象领域.文献[6]将分位数回归方法和变异点分析结合起来，对美国南部月降水的可能变化情况进行了分析.文献[7]运用分位数回归方法研究了波罗的海海平面的长时间变化情况，结果表明，斜率在极大值处表现出更大的趋势性.文献[8]运用分位数回归模型分析了滦河流域降水及径流变化特性.

对于娘子关泉域降水、径流变化特征的研究，文献[9]采用广义极值Pareto分布模型分析月最大降水量，并在剔除人类活动造成的泉水流量下降趋势（平稳化）后，研究不同重现期的极大月降水量与平稳化后的泉水年平均流量的关系，以获得极端降水与泉水流量的相关关系.为了更详细地分析降水、径流的变化情况，本文采用分位数回归方法，在选取的高、低分位数水平下对年降水、径流序列的变化特征进行研究.

1 研究区概况及数据处理

1.1 研究区概况

娘子关泉位于山西省与河北省交界处的平定县娘子关附近，是我国北方最大的岩溶泉之一.其地理位置介于北纬 36°55′～37°50′、 东经 112°20′～113°55′之间.涉及的行政区有阳泉市郊区、平定县、盂县，以及晋中市的和顺县、左权县、昔阳县和寿阳县等7个区域.娘子关泉出露于桃河与温河汇集地段，由11个主要泉组组成，分布自程家村至绵河的苇泽关约7 km长的河漫滩及阶地上，出露标高372～392 m，泉域面积为4 667 km2.

娘子关泉域属暖温带大陆性季风气候，多年平均降水量为534.3 mm，月降水量变化较大，最大月降水量达到341.83 mm（1963年8月）.多年平均径流量为10.4 m3/s（1956—2003年），其中最小月流量为4.69 m3/s（1995年3月），最大月流量为17.30 m3/s（1963年10月）.

1.2 数据处理

考虑到不同地区降水对娘子关泉地下水补给的贡献率[10]以及不同地区的面积，首先采用泰森多边形加权平均的方法求得2个时间段内的降水权重.1959—1971年6个雨量站的降水权重分别为：阳泉（0.38）、盂县（0.35）、寿阳（0.09）、昔阳（0.10）、和顺（0.05）、左权（0.03）.1971—2009年 7个雨量站的降水权重分别为：阳泉（0.30）、盂县（0.15）、寿阳（0.09）、昔阳（0.10）、和顺（0.05）、左权（0.03）、平定（0.28）.

2 研究方法

2.1 分位数回归方法

给定一个连续型一元随机变量Y，其分布函数为FY（y），则其τ分位数定义为

其中 τ∈（0，1）.

设给定X下Y的τ条件分位数[11]为

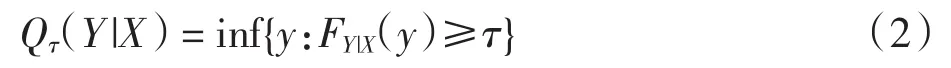
其中FY|X（y）为连续型随机变量Y在给定X下的条件分布.显然，Qτ（Y|X）是X的函数，记为

取g（X）为线性函数，即

其中 β（τ）是未知参数.参数 β（τ）满足如下关系

批而未供和闲置土地大清查大处置工作虽然取得了阶段性成果，但推进批而未供土地消化利用和闲置土地处置工作不能松懈。要举一反三，常抓不懈，以本次行动为契机推进长效机制的建设。下一步，重点抓好以下几个方面工作。

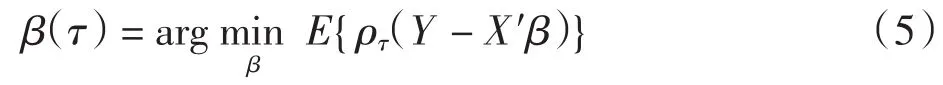
其中：ρτ（z）=z（τ-I（z<0））称为对号函数（check function），I（·）为示性函数.容易看出，ρτ（z）是一个非对称的损失函数.当τ=1/2时，式（5）即为最小一乘回归.

给定观测数据（x1，y1），（x2，y2），…，（xn，yn），分位数回归通过最小化损失函数来求解参数估计值.由下式求解τ分位数的回归估计：

式（6）也可以写作：

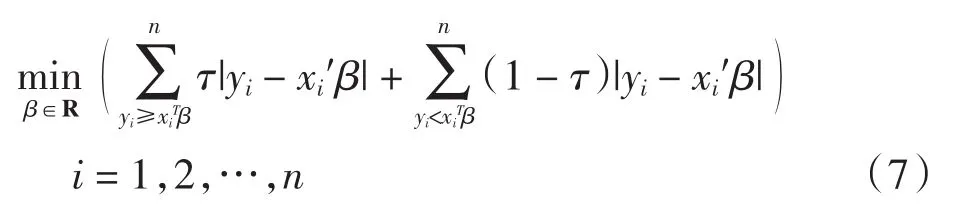
参数β（τ）的估计可以通过下式得到：

2.2 分布变化分析方法

多条分位数回归线表现出的回归趋势会引起不同年份概率分布的变化.因此，需要在得到不同分位点下回归线的基础上，对年降水和年径流序列在不同年份的概率分布变化情况[12]进行分析.具体的分布变化分析过程为：根据分位数回归结果，可以得到不同τ值下的分位数值.选定一个年份，根据年降水和径流序列在不同τ值下的分位数值求得分布函数.然后，根据求得的分布函数，运用自适应核密度估计方法得到概率密度函数.

3 结果与分析

3.1 年降水和年径流的分位数回归分析

为了能够更明显地显示高低分位数水平下年降水指标随时间的变化趋势，在0～1之间每间隔0.05选取一个分位点，其中，分位点为0.50时的回归直线为中位数回归.另外，为了便于对比不同的回归线，拟合了一条线性回归直线.结果见图1～图3，图中自上而下的分位点分别为：0.95，0.90，0.85，0.80，…，0.05.

图1 年降水量随时间的变化趋势Fig.1 Changes trend of annual precipitation over time

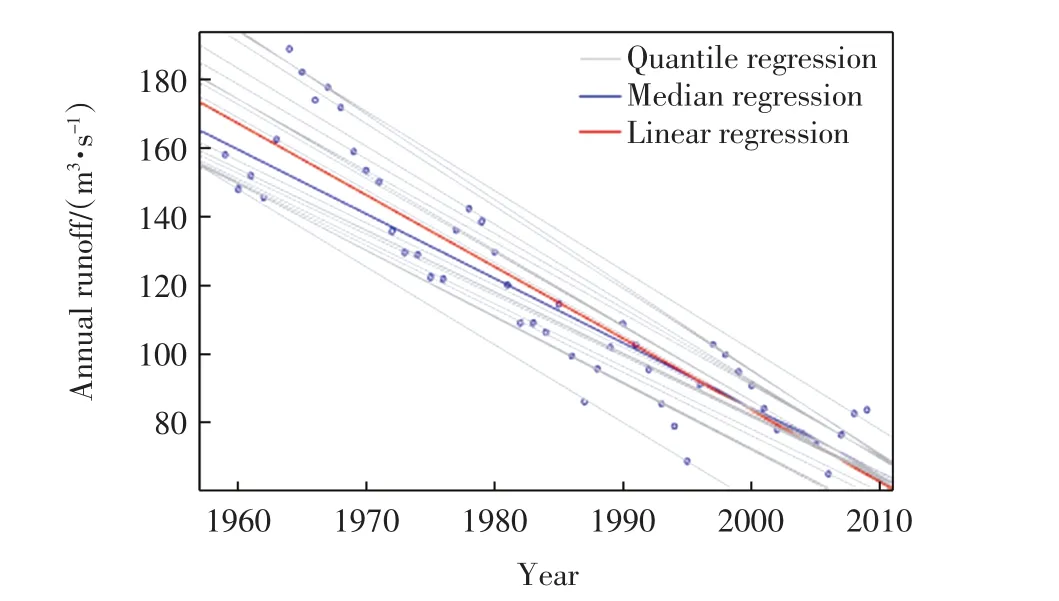
图2 年径流量随时间的变化趋势Fig.2 Changes trend of annual runoff over time

图3 年降水量和年径流量之间的关系Fig.3 Relationship between annual precipitation and annual runoff

观察年降水量随时间的变化趋势（图1）可见，中位数回归直线和线性回归直线几乎重合.绝大多数分位点的回归直线呈下降趋势，当分位点特别低时，年降水量随时间变化不明显，而当分位点为0.05时，年降水量有显著的下降趋势.估算0.05和0.95这2个分位点处的年降水量可得，1959年的年降水量大约分布在406 mm和826 mm之间，2009年的近似最小和最大年降水量分别为264 mm和629 mm.

观察年径流量随时间的变化趋势（图2）可见，中位数回归直线在1995年之前一直位于最小二乘法所得到的回归直线之下，这说明1995年之前的年流量是右偏的.另外，高分位点的分布随时间的变化更为集中，而低分位点的分布随时间的变化更为发散，分位数回归直线左侧和右侧之间的间隙相差不大，这意味着数据点整体较为均匀.回归直线均呈下降趋势，说明年径流量在逐年减少.估算0.05和0.95这2个分位点处的年径流量可得，1959年的年径流量大约分布在150 m3/s和193 m3/s之间，2009年的近似最小和最大年径流量分别为37 m3/s和80 m3/s.

由年降水量和年径流量之间的关系（图3）可见，在绝大多数分位点处，随着年降水量的增加，年径流量呈增加的趋势.而当年径流量特别低时，年径流量随着年降水量的增加反而呈下降趋势.

3.2 年降水和年径流的分布变化

为了解年降水和年径流序列的分布变化规律，在百分位数线性回归的基础上，对序列在特定年份的经验累积分布函数（CDF）以及经验概率密度函数（PDF）进行了分析.由于采用的方法是线性分位数回归方法，所以其他年份的CDF和PDF的变化范围介于第一年和最后一年之间.因此，选取时间序列中第一个年份（1959年）和最后一个年份（2009年）作为代表年份进行研究.结果见图4和图5.

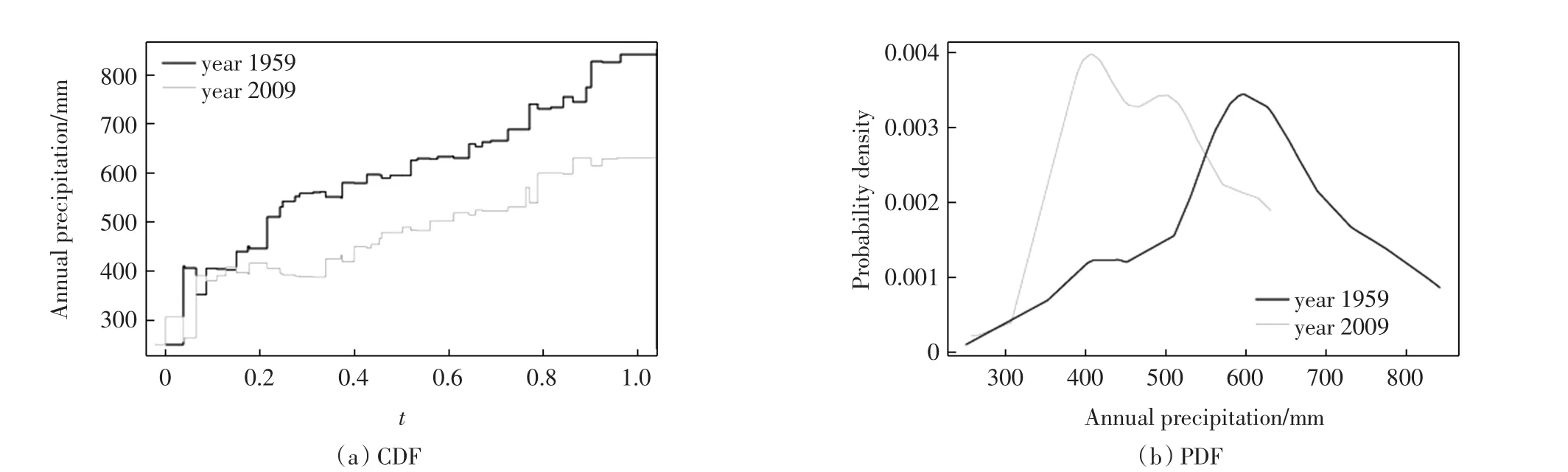
图4 年降水量的经验累积分布函数（CDF）和经验概率密度函数（PDF）Fig.4 Empirical cumulative distribution function（CDF）and empirical probability density function（PDF）of annual precipitation

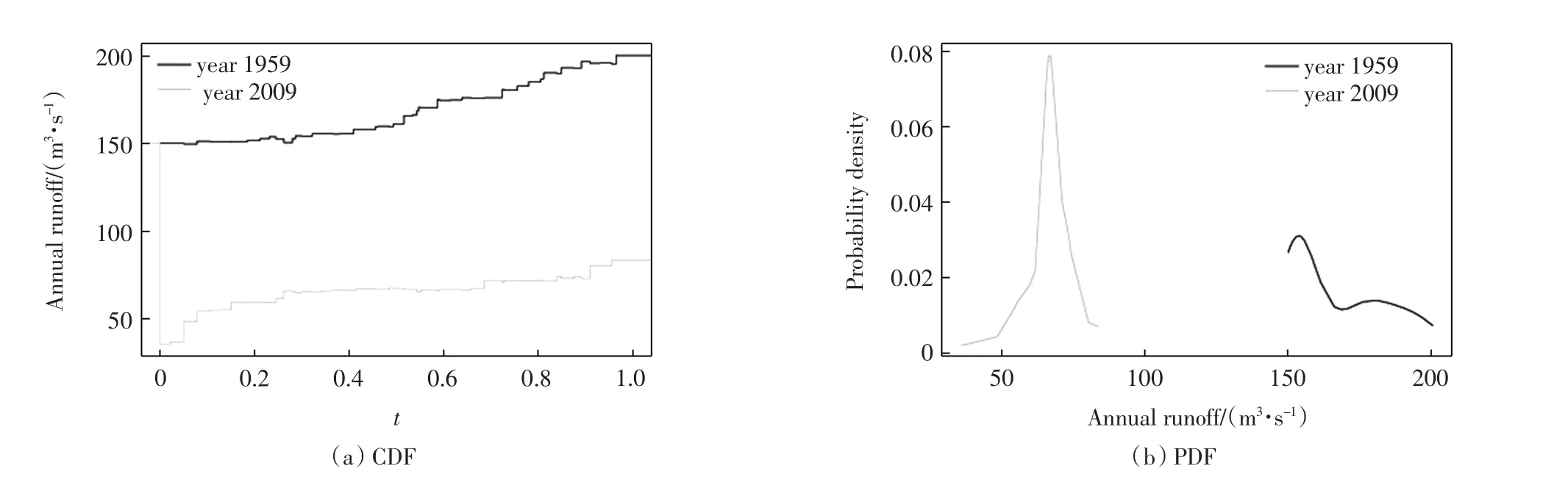
图5 年径流量的经验累积分布函数（CDF）和经验概率密度函数（PDF）Fig.5 Empirical cumulative distribution function（CDF）and empirical probability density function（PDF）of annual runoff

由年降水量的CDF和PDF曲线（图4）可见，2009年的PDF与1959年的相比，不仅峰度发生了变化，从1个峰度变化为2个峰度，其分布的范围也发生了改变.概率密度在1959年的最高值为0.003 5左右，而到2009年变为0.004 0左右，函数分布范围从年降水量400～800 mm左右减少至300～600 mm左右.由图1，年降水量分位数回归线有汇聚并且下降的趋势，因此PDF曲线向左移动.

由年径流量的CDF和PDF曲线（图5）可见，2009年的PDF与1959年的相比，不仅峰度发生了变化，从2个峰度变化为1个峰度，其分布的范围也发生了改变.概率密度在1959年的最高值为0.03左右，而到2009年变为0.08左右，峰值显著变大，函数分布范围从年径流量150～200 m3/s左右减少至20～80 m3/s左右.由图2，年径流量分位数回归线有聚合的变化趋势，且回归直线斜率均为负值，下降趋势明显，因此PDF曲线有很大程度的左移.

4 结论

对娘子关泉域1959—2009年的年降水、年径流资料运用分位数回归方法进行分析，研究年降水和年径流之间的变化特征及其响应关系.在此基础上，对序列在特定年份的分布函数及概率密度函数进行分析，从而了解娘子关泉年降水、年径流序列的分布变化，得出如下结论：

（1）年降水序列在绝大多数分位点的回归直线有下降趋势.高分位点的下降趋势总体来说比低分位点的下降趋势更为显著.年径流序列高分位点的回归直线随时间有收敛趋势，低分位点的回归直线随时间有发散趋势，但是整体来说，回归直线都呈下降趋势，说明年径流量在逐年减少.

（2）经估算，1959年的年降水量大约分布在406～826 mm之间，而2009年的年降水量大约分布在264～629 mm之间，1959年的年径流量大约分布在150～193 m3/s之间，而2009年的年径流量大约分布在37～80 m3/s之间.

（3）在绝大多数分位点处，年径流量随着年降水量的增加有增加的趋势.而当年径流量特别低时，年径流量随着年降水量的增加反而呈下降的趋势，这可能是因为受到了人类活动的影响.

（4）2009年与1959年相比，年降水序列的CDF分布范围缩减，PDF曲线向左移动，且从1个峰度变为2个峰度.函数分布范围从年降水量400～800 mm左右减少至300～600 mm左右.年径流序列的PDF曲线左移，从2个峰度变为1个峰度，且峰值显著变大，函数分布范围从年径流量150～200 m3/s左右减少至20～80 m3/s左右.