基于磨耗数据统计模型的镟轮决策优化

杨 志,邢宗义,王 露,龙 静

(1.南京理工大学自动化学院,南京 210094； 2.广州地铁集团有限公司运营总部 ,广州 510380)

基于磨耗数据统计模型的镟轮决策优化

杨 志1,邢宗义1,王 露1,龙 静2

(1.南京理工大学自动化学院,南京 210094； 2.广州地铁集团有限公司运营总部 ,广州 510380)

针对目前地铁车辆车轮等级镟修而导致的镟修不合理问题,提出一种基于磨耗数据统计模型镟轮决策优化方法。基于广州地铁8号线的轮对磨耗数据,首先利用SPSS分析轮径磨耗和轮缘磨耗与轮缘厚相关性；其次建立基于状态转移过程的轮缘磨耗模型和基于数理统计模型的轮径磨耗模型；然后研究单个车轮的单级和多级镟修控制限策略,并通过蒙特卡罗仿真分析比较两种控制限策略的优劣。结果表明,多级镟修控制限策略大大提高车轮使用寿命,节约列车运营成本。

轮对磨耗；优化；单级镟修策略；多级镟修策略

1 概述

随着轨道交通的不断发展，车轮的磨耗一直都是国内外学者关注的问题。Ansari等[1]建立基于多体动力学理论的轮对磨损模型，通过分析德黑兰地铁车辆轮对磨耗数据验证了模型的可行性。Ward等[2]提出基于轮轨动力学的车轮磨耗数据算法，实现车轮磨耗仿真分析。Arizon等[3]采用解析模型对车轮磨耗进行分析，实现车轮磨损故障建模和寿命预测。黄永达[4]和刁晓明[5]通过统计武广高速动车组踏面磨耗数据，分析得出踏面磨耗较大时轮缘厚度的磨耗也较大。上述文献主要从动力学模型和实际磨耗数据等方面进行了大量研究，为车轮镟修优化奠定了基础。

TAO等[6]通过分析D20E型机车车轮的磨耗数据，建立基于数理统计磨耗模型，实现不同类型机车车轮镟修周期预测。Braghin等[7]提出了一种轮对磨耗数值模拟方法，研究表明列车行驶里程达20万km时进行镟修，将有效提高车轮使用寿命。员华[8]、朱士友[9]和孙小康[10]均对等级镟修可行性进行了分析，认为应根据轮缘厚度选择不同的镟修等级。上述方法从车轮磨耗角度进行了统计分析并给出镟修建议，但没有触及车轮镟修决策优化的实质。

由于列车自身车型的不同和运营线路的差异，仅仅基于动力学性能分析来制定车轮的镟修方案无法满足实际应用，而通过统计分析具体线路实际运营中的列车车轮磨耗数据来制定或调整镟轮维修周期是有效可行的。因此，基于广州地铁8号线的磨耗数据进行分析，提出一种车轮多级镟修控制限策略模型，以满足镟轮维修的实际需求。

2 车轮磨耗与轮缘厚相关性分析

许宏[11]、王凌[12]和Ansari M[13]研究表明轨道交通的车轮磨耗速率与轮缘厚度有关，但磨耗率与轮缘厚度的趋势和相关性却不尽相同，车轮磨耗情况与列车型号、运营线路环境、车轮材质等多种因素相关。因此，建立车轮磨耗模型之前需要对轮径磨耗和轮缘磨耗相关性进行分析。

将广州地铁8号线列车的轮对尺寸数据作为样本数据进行分析，由式(1)和式(2)计算每间隔30 d轮径磨耗率和轮缘磨耗率

式中，Di+1和Di分别为不包含镟轮情况下ti+1和ti时刻轮径测量值；Sd，i+1和Sd，i分别为不包含镟轮情况下ti+1和ti时刻轮缘厚度测量值；vd，i和vsd，i分别表示各个时间段轮径磨耗率和轮缘磨耗率。

为了方便分析车轮磨耗与轮缘厚度的相关性，将vd，i近似成轮径为(Di+1-Di)/2的轮径磨耗率，同理，vsd，i近似成轮缘厚度为(Sd，i+1-Sd，i)/2的轮缘磨耗率。

本文利用SPSS软件分别对轮径磨耗率和轮缘磨耗率与轮缘厚度的相关性进行分析，通过对式(1)和式(2)近似得到的轮径磨耗率和轮缘磨耗率进行统计计算，得到轮径磨耗率与轮缘厚度皮尔森相关性为-0.05，而轮缘磨耗率与轮缘厚度皮尔森相关性为-0.286，因此可以认为轮缘磨耗率与轮缘厚度是相关的，而轮径磨耗率与轮缘厚度是独立的。

3 轮缘磨耗模型和轮径磨耗模型

根据轮缘磨耗率与轮缘厚度相关，轮径磨耗率与轮缘厚度相互独立的分析结论，分别对车轮轮缘和轮径的磨耗规律进行建模。

3.1 基于状态转移过程的轮缘磨耗模型

根据地铁车辆轮对尺寸安全限度要求：轮缘厚度Sd应满足26 mm≤Sd≤32 mm，将轮缘厚安全域分为20个以0.3 mm为长度的状态区间，分别为：(31.7，32]，(31.4，31.7]，(30.1，31.4]，…，(26.3，26.6]，[26，26.3]，各状态分别记为S1，S2，…S20。

将上述均匀时间间隔的轮缘厚度样本数据进行多状态区间统计，在车轮经过30 d磨耗后，轮缘厚度会发生一定的改变。由于车轮磨耗存在大小差异，因此，经磨耗的车轮轮缘厚度值可能会停留在原状态区间，记为S(i，i)，也有可能转移至另外一个状态区间，记为S(i，i+m)，状态转移示意如图1所示。

由于每个状态区间长度均为0.3 mm，若车轮在30 d磨耗后为状态停留，对应磨耗量为0～0.3 mm，若为状态一级转移，则对应磨耗量为0.3～0.6 mm，若为状态二级转移，则对应磨耗量为0.6～0.9 mm，以此类推。将样本数据根据状态转移方式进行统计，得到各状态转移的频数统计情况，进而得到每个初始状态对应的状态转移概率。由于状态变换情况主要集中在状态停留、状态一级转移、状态二级转移，为方便分析，舍弃三级转移及三级以上的小概率状态转移情况。将状态停留、状态一级转移、状态二级转移根据统计权重进行重新分配，得到调整后的状态转移概率表，如表1所示。

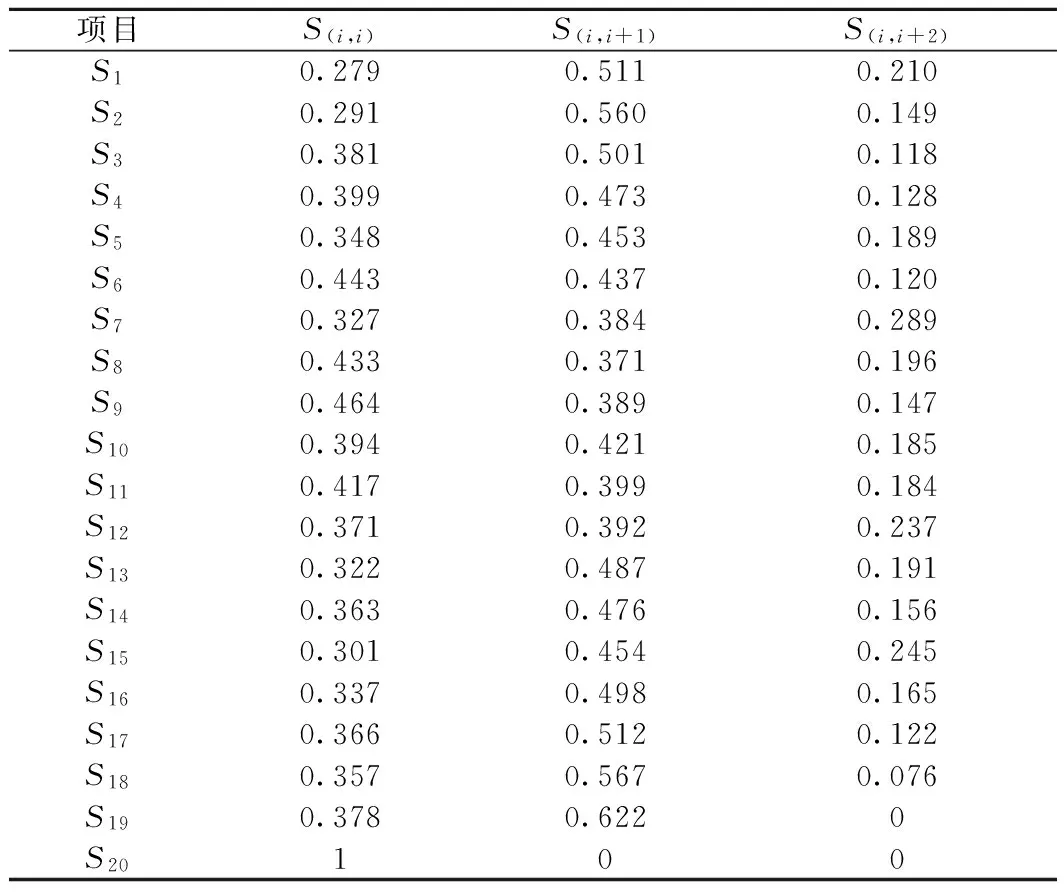
表1 简化状态转移概率

从表1可以得出，状态二级转移的概率基本保持在一个稳定范围内，说明异常磨耗情况是相对稳定的。而状态停留、状态一级转移会随轮缘厚度的变化有明显的变化趋势，且轮缘磨耗率与轮缘厚度之间相关性较大，因此二者存在一定的变化规律。根据表1作图2观察状态停留和状态一级转移下轮缘磨耗随轮缘厚度的变化规律。

图2 轮缘磨耗与轮缘厚度趋势变化曲线

图2为磨耗规律拟合曲线，能大致反映轮缘磨耗随轮缘厚度变化过程。状态停留概率随轮缘厚度的减小呈现先增大再减小趋势，在初始状态S6～S9范围内时，其状态停留概率较大，说明其磨耗率越低。从总体趋势上看，状态停留轮缘磨耗随轮缘厚度的减小呈先减小再增大的趋势。而由于状态二级转移概率基本稳定，因此状态一级转移的变化规律必然与状态停留变化规律呈相反趋势。

通过统计各初始状态下经过磨耗的状态转移概率，可以得到车轮轮缘磨耗过程中每个初始状态分别对应3种转移的可能性，每种转移的可能性由统计的概率决定，满足均匀分布。

3.2 基于数理统计理论的轮径磨耗模型

根据广州地铁8号线近5年轮径磨耗率数据进行统计分析，得出轮径磨耗率基本在-3～3 mm/30 d，为方便统计分析，将区间[-3,3]平均分为60个小区间，每个区间长度为0.1 mm。对每个区间内的轮径磨耗率的频数进行统计，得出如图3所示轮径磨耗率统计直方图。其中，轮径磨耗率在-0.2～-0.1 mm/30 d的频数最大，主要集中在-0.3～0.1 mm/30 d，轮径磨耗率向两侧延伸，磨耗率频数逐渐减小。

为得到轮径磨耗率统计规律，分别采用正态分布、对数正态分布、威尔布分布和Γ分布对轮径磨耗进行建模。将轮径磨耗率频数统计结果导入Matlab中，可以拟合计算得到4种分布概率密度函数具体参数。

图3 轮径磨耗率频数统计直方图

正态分布概率密度函数

式中，μ=-0.173 3，σ=0.543 8。

对数正态分布概率密度函数

式中，μ=1.0188，σ=0.2134。

威布尔分布概率密度函数

式中，α=4.8187，β=0.0047。

Γ分布概率密度函数

式中，α=24.8086，β=0.1139。

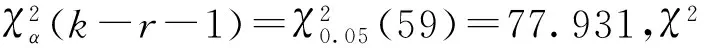
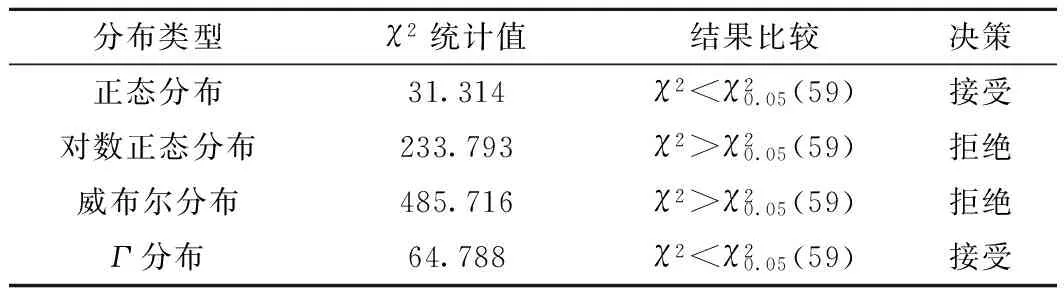
表2 拟合优度检验结果

根据表2可以得到，通过χ2拟合优度检验，轮径磨耗分布服从正态分布和Γ分布，而对数正态分布和威布尔分布有显著差异。因此舍弃对数正态分布和威布尔分布模型，对正态分布和Γ分布进行比较分析。

根据图3知轮径磨耗率频数在-0.2～-0.1 mm/月所占比例最大，而由各分布的概率密度函数可得正态分布和Γ分布分别在轮径磨耗率为-0.173 3 mm/月和-0.301 6 mm/月时所占比例最大，可知正态分布更符合轮径磨耗分布。且通过计算实际轮径磨耗率在-3～1 mm/30 d概率与正态分布和Γ分布进行比较，得出实际轮径所占总体概率为0.974 6，而正态分布和Γ分布分别为0.984 5和0.954 7。综上计算结果，确定正态分布为轮径的磨耗模型。

4 单轮等级镟修控制限策略模型

通过轮缘磨耗模型和轮径磨耗模型模拟仿真车轮磨耗过程，建立单个车轮的单级和多级镟修控制限策略模型，并通过蒙特卡罗仿真对比分析两种策略方案优劣得出最优的控制限策略方案。

4.1 单级镟修控制限策略模型

单个车轮的镟修策略模型主要考虑车轮的轮缘厚度的控制限范围，即车轮何时镟修，镟修恢复至多少，两者分别对应轮缘厚度控制限的下限和上限。在建立轮缘磨耗模型时提出了状态转移的概念，并对车轮轮缘厚度的安全阈进行了状态划分，现做出如下描述：当车轮的轮缘厚度磨耗至某一状态Sj，再将其恢复至某一状态Si。其中，Si对应控制限上限状态，记为Sh；Sj对应控制限下限状态，记为Sl，且控制限上下限状态分别对应各自的区间范围，其区间分别表示为[Shr，Shl]和[Slr，Sll]。

单级控制限仅对应一个上限和一个下限，即车轮轮缘厚度磨耗至一个统一的下限，恢复至同一个上限。当车轮的轮缘厚度经过一个磨耗周期(30 d)磨耗至小于等于控制限下限状态区间左值Sll时，对车轮进行镟修，将轮缘厚度恢复至控制限上限状态区间Shl处，单个车轮单级镟修控制限策略示意如图4所示。轮缘在磨耗过程中，遵循轮缘磨耗状态转移概率表。

图4 单级镟修控制限策略示意

根据车轮单级镟修控制限原理计算得到单级镟修有210种策略方案。本文镟修控制限策略的制定原则是保证轮缘厚度维持在26～32 mm安全阈范围内，同时得到较优的控制限策略，以延长车轮的使用寿命并保证较小的镟修次数。因而将车轮使用寿命和镟修次数作为优化目标，经过蒙特卡罗仿真得到每种镟修策略方案的期望使用寿命和期望镟修次数，从而选出较优的策略方案，仿真流程如图5所示。

图5 单级镟修控制限蒙特卡罗仿真流程

单级镟修蒙特卡罗仿真步骤如下。

①参数初始化：设置未经磨耗的车轮轮径和轮缘厚度初始值分别为D(0)=840 mm，Sd(0)=32 mm，寿命累计周期T=0，镟修次数N=0，两次镟修间隔时间t=0；控制限上下限状态区间为Sh和Sl，对应镟修恢复上下限值为Shl和Sll，此处将分别导入210种策略对应的值。

②本次磨耗时间周期累计t=t+1。

③根据T+t-1时刻的车轮轮径值D(T+t-1)和轮缘厚度值Sd(T+t-1)，由轮径磨耗正态分布模型随机生成轮径磨耗概率pD以及状态转移概率均匀分布随机生成状态转移概率pSd，并根据磨耗概率得到轮缘磨耗率vd和轮径磨耗率vSd，通过D(T+t)=D(T+t-1)-vd和Sd(T+t)=Sd(T+t-1)-vSd计算当前时刻轮径值和轮缘厚度值。

④判断当前时刻轮径值D(T+t)是否≥770 mm，若是，则转入第⑤步，否则结束此次仿真，得到最后的寿命累积周期Tend和镟修次数Nend。

⑤判断当前时刻轮缘厚度值Sd(T+t)是否小于Sll，若是，转入第⑥步，否则转入第②步。

⑥对车轮进行镟修，恢复轮缘厚度至Shl，并对参数进行初始化：T=T+t，N=N+1，t=0，D(T)=D(T)-k×(Shl-Sd(T))，Sd(T)=Shl，初始化完成后转入第②步。其中，k为镟修比例系数，根据庞松林[14]和赵文杰[15]研究成果，取镟修比例系数为4.2。

4.2 多级镟修控制限策略模型

单级控制限策略在镟修过程中以损失较大车轮直径为代价，缩短车轮使用寿命，且单级控制限策略仅针对单个车轮，若因为单个车轮磨耗超过控制限下限就进行镟修工作，则会造成列车频繁下线，给实际镟修工作和运营计划带来困难。因此，为了延长列车使用寿命以及满足实际镟修需求，提出多级镟修控制限策略模型。

对应单级镟修控制限，多级镟修控制限有多个镟修上限和多个镟修下限，并且上限和下限成对出现，多级控制限策略示意如图6所示。

图6 多级镟轮控制限示意

在多级镟修控制限模型中，控制策略种类繁多，两级控制镟修控制限策略有1 140种，三级控制镟修控制限策略有3 876种。为简化工作以及检验方法的有效性，以两级镟修控制限策略为例进行蒙特卡罗仿真。与单级镟修控制限策略仿真过程不同，两级镟修控制限策略初始化时需要对两级镟修上下限进行设置。在判断镟修条件时会进行两级轮缘厚度阈值范围判断，即当前轮缘厚度如果满足一级镟修条件则进行一级镟修，如果当前轮缘厚度值不满足一级镟修条件，则转入二级镟修条件进行判断，并进行相应的操作。通过上述过程实现单个车轮的多级镟修控制限策略仿真。

5 仿真与结果分析

对单级和两级镟修控制限进行蒙特卡罗仿真分析，每种策略方案设置1 000次的仿真次数，取均值得到每种策略方案的期望使用寿命E(T)和期望镟修次数E(N)。

单级镟修控制限策略仿真如图7所示。其中图7(a)为210种策略方案编号示意，且红点代表控制限上限左值，蓝点代表控制限下限左值。图7(b)和图7(c)分别为每种策略方案所对应的车轮期望使用寿命周期和车轮期望镟修次数。

图7 单级镟修控制限策略仿真结果

根据单级镟修控制限策略仿真图可以得出以下结论。

①车轮最大使用寿命策略方案编号为137，最小镟修次数策略方案编号为20，可知使用寿命最大方案镟修次数却不是最小，同理镟修次数最小方案使用寿命却不是最大。因此在选择镟修方案应综合考虑使用寿命和镟修次数。

②在下限值相同的镟修方案，随着上限值增加，车轮使用寿命呈先增大后减小过程，与状态转移概率分布中状态停留概率随轮缘厚度先增大后减小的现象相符。

③在下限值相同的镟修方案中，随着上限值增加，车轮的期望镟修次数均随镟修上限值的增大而减小，即镟修策略上下限之间差值越小，期望镟修次数反而越大。

综合考虑车轮的期望使用寿命和镟修次数，针对单个车轮的单级镟修控制限策略选出4种较优方案，如表3所示。

表3 单级镟修控制限策略较优方案

单个车轮两级镟修控制限策略多达1 140种，但由单级镟修控制限策略仿真结果可知，车轮的期望寿命与状态转移概率分布中的状态停留概率相关，控制限中状态停留概率越大，则对应的车轮期望使用寿命越大。根据图2可知，状态停留概率较大的状态主要为S6～S9，则当一级镟修控制限范围与二级镟修控制限范围过大或过小都不利于车轮使用寿命，因此选择一级控制限下限值和二级控制限上限左值都比较集中的情况进行分析。

选取控制限策略方案编号为749～832进行分析，此时一级控制限下限左值为29.9，二级控制限上限左值为29.6，其两级镟修控制限策略仿真结果如图8所示。其中图8(a)为从749～832对应的84种策略方案的编号示意，图8(b)和图8(c)分别为每种方案所对应的期望使用寿命和期望镟修次数。

图8 两级镟修控制限策略仿真结果

根据两级镟修控制限策略仿真图可以得出以下结论：

①与单级镟修控制限策略仿真类似，使用寿命最大方案镟修次数却不是最小，镟修次数最小方案使用寿命却不是最大；

②在二级控制限上下限值相同时，随着一级控制限上限值增大，车轮期望使用寿命先增大后减小，镟修次数随上限值的增大而减小；

③随着二级控制限下限值的增大，期望使用寿命整体趋势先增大后减小，而镟修次数整体趋势增大。

综合考虑车轮的期望寿命和期望镟修次数，针对两级控制限策略优选出4种较优的方案，如表4所示。

对比单级与多级镟修控制限策略，多级控制限策略总体优于单级控制限策略，主要表现在以下两个方面：

(1)从运营成本的角度，多级控制限策略的车轮期望使用寿命较单级控制限策略长，因此能更有效地节约列车的运营成本；

(2)从实际应用角度，多级控制策略的期望镟修次数虽然提高不大，并且随着二级控制限下限值增大的同时，期望镟修次数总体也呈增大的趋势，但却增加了镟修时间的灵活性，更易于应用于实际作业。

表4 两级镟修控制限策略较优方案

6 结论

本文研究了一种基于磨耗数据统计模型的镟轮决策优化方法，建立了基于状态转移过程的轮缘磨耗模型和基于数理统计理论的轮径磨耗模型，并在此基础上建立单个车轮单级和多级控制限镟修策略模型。通过蒙特卡罗仿真得到多级镟修策略模型将有效提高车轮使用寿命，节约列车运营成本。在研究过程中，仅对两级镟修策略进行研究，未对三级及三级以上镟修进行仿真分析，未检验是否有更优的多级控制限策略。

[1] M Ansari， I A Hazrati， E Esmailzadeh， et al. Wear rate estimation of train wheels using dynamic simulations and field measurements[J]. Vehicle System Dynamics， 2008， 46(8):739-759.

[2] A Ward， R Lewis， R S Dwyer. Incorporating a railway wheel wear model into multi-body simulations of wheelset dynamics[J]. Tribology， 2003，41(3):367-376.

[3] J De Arizon， O Verlinden， P Dehombreux. Prediction of wheel wear in urban railway transport: comparison of existing models[J]. Vehicle System Dynamics， 2007，45(9):849-866.

[4] TAO VAN CHIEN，李芾，戚壮，等.机车车轮磨耗统计数据处理方法与镟修周期预测模型[J].铁道学报，2015(12):14-19.

[5] 黄永达.武广客专轮对磨耗规律分析[J].甘肃科技，2012，28(18):48-49.

[6] 刁晓明，朱韶光，董孝卿.武广客专动车组车轮磨耗及振动性能跟踪研究[J].铁道机车车辆，2013(2):1-6.

[7] F Braghin， R Lewis， R S Dwyer Joyce， et al. A mathematical model to predict railway wheel profile evolution due to wear[J]. Wear， 2006， 261(11-12):1253-1264.

[8] 员华，肖胜强，汪洋.基于磨耗量统计的轮对等级镟修可行性分析[J].城市轨道交通研究，2006，9(1):43-45.

[9] 朱士友，潘丽莎，员华.轮对等级镟修对车辆平稳性的影响分析[J].城市轨道交通研究，2006，9(7):46-48.

[10] 孙小康.地铁轮对踏面镟修经济性分析[J].城市轨道交通研究，2016，19(5):91-92.

[11] 许宏，员华，王凌，等.基于高斯过程的地铁车辆轮对磨耗建模及其镟修策略优化[J].机械工程学报，2010，46(24):88-95.

[12] 王凌，员华，那文波，等.基于磨耗数据驱动模型的轮对镟修策略优化和剩余寿命预报[J].系统工程理论与实践，2011，31(6):1143-1152.

[13] M Ansari， I H Ashtiyani. Determination of the train wheel wear trend， comparing with field measurements[C]∥ Rail Conference， 2006. Proceedings of the 2006 IEEE/ASME Joint. IEEE， 2006:103-107.

[14] 庞松林.CRH2型高速动车组车轮镟修策略的研究[D].北京：北京交通大学，2016.

[15] 赵文杰.地铁车辆轮对磨耗故障预报和镟修策略优化[D].杭州：中国计量学院，2014.

Optimization of Wheel Re-profiling Strategy Based on Statistical Wear Model

YANG Zhi1, XING Zong-yi1, WANG Lu1, LONG Jing2

(1. College of Automation, Nanjing University of Science and Technology, Nanjing 210094, China; 2. Guangzhou City Underground Railway Corporation, Guangzhou 510380, China)

Aiming at improving the current unreasonable wheel-set re-profiling schedule due to class-lathing, a re-profiling strategy is proposed based on historical wear data. Firstly, the SPSS is used to analyze the interdependency between wheel diameter wear and wheel flange width based on the wheel wear data of Guangzhou Metro Line 8. Secondly, flange width wear model based on state transition and wheel diameter wear model based on mathematical statistics are built separately, and single-stage and multi-stage planned turns strategies of individual wheels are studied based on the two models. Finally, Monte Carlo simulation is conducted to compare the two strategies, and the result shows that multi-stage planned turns strategy can prolong expected life of wheels and save operating cost effectively.

Wheel-set wear; Optimization; Single-stage planned turns strategy; Multi-stage planned turns strategy

1004-2954(2018)01-0142-06

2017-03-17；

2017-06-22

国家重点研发计划项目(2016YFB1200402)，广州市产学研协同创新重大专项(201508010010)，国家工程实验室建设项目(2016582)

杨 志(1992—)，男，江苏连云港人，硕士研究生，从事轨道交通车辆检测分析研究，E-mail:1145026112@qq.com。

U455.43

A

10.13238/j.issn.1004-2954.201703170006