多关节机械臂轨迹跟踪自适应神经网络滑模控制

钱 前，张爱华

(上海工程技术大学机械与汽车工程学院，上海 201620)

0 引言

机械臂控制系统具有强耦合性和复杂的非线性，系统中存在的不确定干扰和建模误差会降低控制性能。传统的控制方法难以保证控制效果和控制精度[1-2]。滑模控制通过控制量的切换，使系统状态能够沿着滑模面运动，具有对外部扰动以及参数变化的高度适应等优点。径向基函数(radial basis function,RBF)神经网络控制具有对任意不确定非线性函数逼近的优点。因此，具有强鲁棒性滑模控制与神经网络控制相结合的方法广泛应用于机械臂控制系统[3-10]。

本文提出一种自适应神经网络滑模控制方法，对滑模控制添加指数趋近律，并使用RBF网络逼近不确定项。为了更好地削弱因误差而引起的抖振、提高系统鲁棒性，添加了一个神经网络逼近误差自适应补偿控制项。采用李雅普诺夫稳定性理论证明系统的稳定性，并通过仿真验证了该方法的有效性。

1 多关节机械臂数学模型

对于n关节的机械臂，考虑外界扰动和建模误差影响，并利用拉格朗日方程建立机械臂数学模型[11-12]：

(1)

(2)

2 自适应神经网络滑模控制器

2.1 滑模控制器

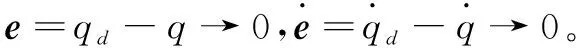
n关节机械臂系统的跟踪误差表示为：

(3)

设计滑模面：

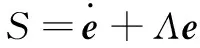
(4)

式中：Λ=diag{λ1,λ2,…,λn}，λ1,λ2,…,λn>0。

对式(4)求微分：

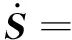
(5)

设计控制变量：

(6)

为滑模添加指数趋近律，令：

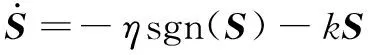
(7)

式中：η>0;k>0。

根据等价控制设计控制器：

u(t)=u1+u2

(8)

(9)

将式(6)、式(7)和式(8)代入式(5)，得到：

(10)

选择李雅普诺夫函数：

(11)

对其求微分，并代入式(10),得到：

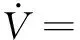
(12)

根据李雅普诺夫稳定性理论可知，系统是全局稳定的。

2.2 自适应神经网络滑模控制器

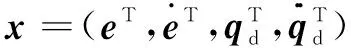
(13)

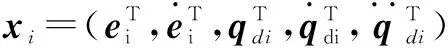
(14)

式中：φ(x)=[φ1,φ2,…,φn] 为高斯基函数的输出；g(x)=exp(-x)为高斯基函数；ci、σi为高斯基函数的中心值和基宽；θ为神经网络权值。

定义ζ为神经网络逼近存在误差，则有：

(15)

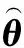
设计神经网络权值的自适应律,为:

(16)

式中：Γ∈Rn×n为调整系数。

由于此处存在学习误差，特别当网络结点较少时会出现较大误差，故重新设计自适应神经网络滑模控制律为u=u1+u2+u3。

(17)

式中：u3为神经网络逼近误差的自适应补偿控制项。

(18)

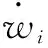
对RBF网络逼近时,作以下合理假设。

假设1 RBF网络逼近存在一个最优权值θ*，使：

ρ(t)=θ*Tφ(x)+ε

(19)

假设2 RBF网络的输出是连续的，并且存在一个特别小的实数ε0，使式(20)成立：

(20)

3 稳定性分析

定义理想的逼近权值为θ*，有:

(21)

选择RBF网络理想逼近误差,为：

ρ(t)-ρ(x,θ*)=w*

(22)

最佳逼近权值与实时权值误差为：

(23)

补偿误差的自适应控制器的误差为：

(24)

选择李雅普诺夫函数为：

(25)

求微分可得：

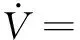
(26)

4 仿真研究

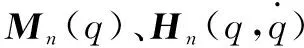
(27)

(28)

(29)

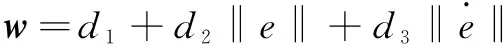
RBF神经网络采用5个输入单元、7个中间单元、2个输出单元的结构。其中：基宽b=2,c=[-3 -2 -1 0 1 2 3] ，自适应调节矩阵为Γ=diag{5,5}。控制器中参数如下：η=0.8,k=diag(50,50),rw=1。设定仿真时间为10 s，仿真步长为0.01 s，进行相关仿真。

图1与图2为无扰动的双关节轨迹跟踪与角速度跟踪图。从图2可以看出，系统能以一定速度收敛到平衡点，大大削弱因干扰而引起的抖振，同时能实现良好的轨迹跟踪与角速度跟踪。

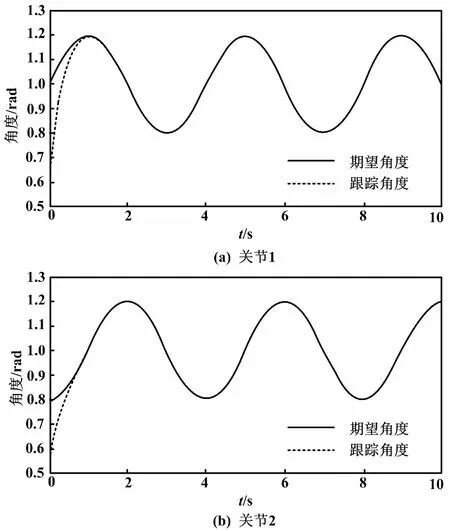
图1 双关节轨迹跟踪图(无外部扰动)

图2 双关节角速度跟踪图(无外部扰动)

图3为无扰动的双关节控制力矩图。从图3可看出，系统对关节的控制力矩平稳，几乎无抖振，可避免机器因抖振而损坏。

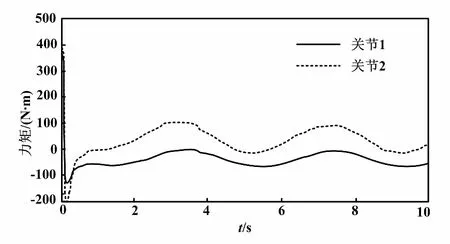
图3 双关节控制力矩图(无外部扰动)

图4与图5为加强外部扰动情况下的双关节轨迹跟踪与角速度跟踪图。从图4和图5可以看出，系统在加强外部扰动情况下，仍可保持良好平稳的轨迹跟踪与角速度跟踪。

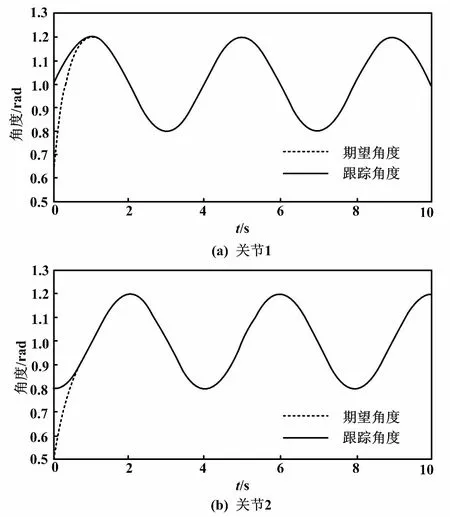
图4 双关节轨迹跟踪图(有外部扰动)

图6为加强外部扰动情况下双关节的控制力矩图。从图6可以看出系统对关节的控制力矩仍然保持平稳，虽在3.5～4 s之间出现轻微抖振现象，但可通过本文提出的控制方法进行自适应调节，达到良好的抑制效果。

图5 双关节角速度跟踪图(有外部扰动)

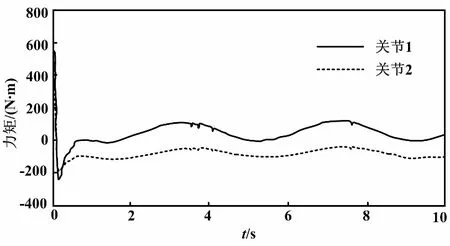
图6 双关节控制力矩图(有外部扰动)

5 结束语

本文提出了一种自适应神经网络滑模控制算法，可解决存在不确定性和系统建模误差的多关节机械臂跟踪控制问题。通过自适应项改进神经网络对不确定项ρ(t)的逼近效果，并引入指数趋近率，改善了控制器的响应速度；通过李雅普诺夫稳定性理论，证明了系统的稳定性；通过调节参数，保证了系统的稳定性。MATLAB仿真试验表明，当外部扰动变大时，控制算法可以实现对期望轨迹的稳定跟踪，具有较好稳定性与鲁棒性。