弹道导弹过关机点状态估计方法研究*

杜广洋，郑学合

(1. 北京电子工程总体研究所，北京 100854；2. 中国航天科工集团有限公司 第二研究院，北京 100854)

0 引言

对弹道导弹目标探测跟踪信息的运用是弹道导弹防御的基础。当雷达对弹道导弹目标进行跟踪时，主动段和自由飞行段的运动学模型差别很大，文献[1-4]采用不同的弹道导弹助推运动模型进行跟踪，文献[5-7]研究了雷达跟踪弹道导弹自由飞行段问题。很难用单个的数学模型来描述这2个运动阶段，因此文献[8-10]提出利用交互式多模型(IMM)方法，多滤波器之间通过模型概率更新实现对目标的自适状态估计，同时利用模型概率实现了对过关机点状态的估计。但是，交互式多模型方法计算复杂，并且与雷达探测耦合紧密，难以在类似指控中心这样的信息综合处理机构实现。根据弹道导弹防御的需要，除了要求进行稳定跟踪外，还希望能够利用雷达跟踪信息完成对导弹精密轨迹、弹道参数、识别信息等的估计。因此，对导弹过关机点状态的准确及时估计，对于跟踪信息处理方式的切换意义重大。

本文从指控信息处理中心的应用出发，基于雷达跟踪信息，提出将推力加速度作为特征量估计导弹过关机点状态，并推导了观测方程。针对观测方程非线性问题，通过对多个随机变量的线性化，利用递推最小二乘(RLS)算法获得了推力加速度的递推估计。通过误差分析，给出了过关机点状态估计门限计算方法。仿真表明，该估计方法能够给出比较理想的过关机点状态估计结果。

1 弹道导弹过关机点状态的特征量

1.1 推力加速度特征量分析

1.2 观测方程

本节将根据雷达跟踪信息推导推力加速度状态的观测方程。

(1)

式中：μ=3.986 004 418×1014(m3·s-2)为地球引力常数。

对式(1)求时间微分可得能量的质量/时间密度为

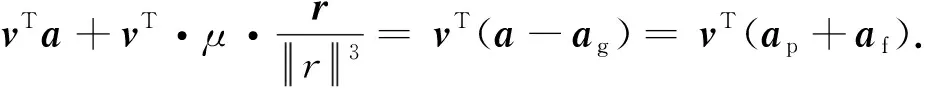
(2)

文献[9]通过推力和阻力参量敏感度分析得出结论，与推力相比，阻力的敏感度较低，作用可忽略。所以，式(2)可近似为Emt≈vTap，即向量v与向量ap的内积。设向量v与向量ap的夹角为α，即攻角，那么导弹完成程序转弯后，推力加速的导弹一般攻角α控制得很小，推力的方向可近似为沿着导弹的速度方向[12]，即α≈0。通过这2次近似，式(2)可化简为

(3)

为了求取能量的质量/时间密度Emt，取当前时刻前n组数据，则其等间隔线性最小二乘拟合解为

(4)

式中：Δt为数据采样间隔。

将式(4)带入式(3)即为推力加速度的观测方程为

(5)

根据雷达输入的位置、速度信息，利用式(5)和式(4)即可计算当前时刻的推力加速度。从形式上看，推力加速度状态量可以看做是能量的质量/时间/速度密度。

2 推力加速度的估计

2.1 观测方程的线性化

(6)

(7)

式(7)就是线性化后的推力加速度观测方程。

,

(8)

2.2 推力加速度的最小二乘估计及其递推公式

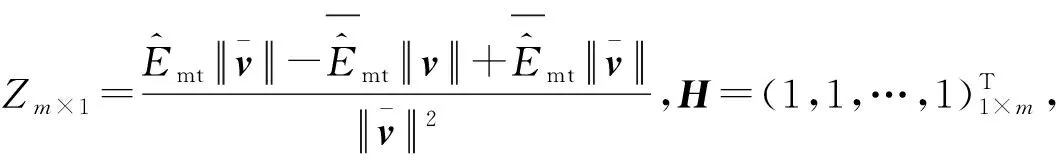
(9)

为了方便在指控中心计算，下面给出递推最小二乘(RLS)公式[14]为

(10)

3 过关机点状态检测门限选取

在关机时刻前后，推力加速度ap的退出带来的运动状态发生显著变化，因此可以通过选取适当的检测门限判断弹道导弹目标是否过了关机点。推力加速度的估计过程中产生的估计误差主要包括2项：①线性化引入的误差；②最小二乘估计误差。其他如推力方向与速度方向重合近似等带来的误差均可忽略不计。

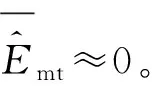
(11)

(12)

将式(11)和式(12)合成为推力加速度估计误差为

(13)

式中：

(14)

一般雷达报送指控的位置与速度均为估计结果，且具有较强的相关性，工程上为了计算方便，忽略相关项(相当于误差容限放大)，则过关机点状态检测门限取为

(15)

式中：α为误差放大系数。

4 仿真分析

利用典型6 00 km，3 000 km射程弹道导弹理论弹道，通过仿真检验本文阐述的弹道导弹过关机点状态估计方法的有效性。雷达向指控信息处理中心报送的状态量为具有一定相关性位置和速度信息。指控信息处理中心根据雷达观测结果估计弹道导弹目标的过关机点状态。仿真参数见表1所示。

表1 仿真参数

根据雷达报送的观测结果，分别计算2种射程下的弹道导弹目标的能量信息，包括：①能量的质量密度；②能量的质量/时间密度；③能量的质量/时间/速度密度。仿真结果见图2。由图2a)和图2b)可见，2种射程下能量的质量密度和能量的质量/时间密度差别都很大，在未知射程的情况下，很难根据雷达的探测误差能力给出统一的判决门限，从而有效区分是否过关机点状态。由图2c)可见，在自由飞行段，不同射程下的能量的质量/时间/速度密度观测结果是趋于一致的，这就为根据雷达的探测误差能力给出统一的判决门限创造了良好的条件。根据本文式(3)的论述，能量的质量/时间/速度密度可近似为推力加速度。仿真结果证实了本文将推力加速度作为判断过关机点状态特征量的正确性。

利用本文提出的推力加速度的估计方法和检测门限的选取方法，对表1仿真参数下的2种射程进行了仿真。仿真结果见图3。图3中，横坐标为弹道导弹发射时间，纵轴为推力加速度。利用雷达跟踪的位置与速度信息，导出推力加速度特征量，如图3绿色曲线所示。从弹道导弹发射起始直到自由飞行段，对雷达观测导出特征量进行RLS递推估计，结果如图3黑色曲线所示。实时检测门限如图3红色曲线所示。从仿真结果可见：在2种射程条件下，利用雷达观测对推力加速度的实时估计结果与真值吻合程度较好，检测门限选取合理，过关机点状态区分度较好，弹道弹道关机后2 s给出了过关机点状态变化估计结果。这一滞后时间与雷达输入的观测误差和数据率有关系，观测误差越小、数据率越高，检测滞后时间越短。

从图3仿真结果可见，在弹道导弹初始加速段，由于推力加速度尚处于较低水平，其真值低于观测误差，因此检测门限失效。对于初始加速段，本文讨论的方法已不再适用。雷达观测误差大小影响体现为不满足条件的海拔高度不同。在此海拔高度以下，该观测精度的雷达将无法准确判断关机状态。

5 结束语

本文提出了一种利用雷达跟踪信息对推力加速度特征量进行估计，从而进行过关机点状态检测的方法。相比于并行多模型方法，利用本文方法给出的状态检测结果进行跟踪信息处理方式的切换，极大简化了处理结构和运算量，更容易在指控信息处理中心实现。仿真表明，该估计方法给出了比较理想的过关机点状态估计结果。