区间数模糊综合评判的UCAV空战威胁评估*

王光辉，徐光达，谢宇鹏，吕超

(海军航空大学a.岸防兵学院;b. 研究生大队，山东 烟台 264001)

0 引言

空战对抗的快节奏、高强度，机载武器的信息化、智能化以及战场信息的复杂化、海量化，对无人作战飞机(unmanned combat aerial vehecle，UCAV)的态势感知与战术决策提出了更加严峻的考验。如何基于当前的战场形势判断对手意图并做出合理的威胁评估是UCAV提升作战效能、打赢现代空战的关键所在。由此可见，深入分析空战威胁评估问题具有重要的军事价值。

威胁评估是指如何评判、估计敌方目标对我方进行侵袭成功的可能性及侵袭时可能造成的毁伤程度[1]。目前很多专家对威胁评估问题进行了研究，成果显著。例如，文献[2]采用熵理论与TOPSIS相结合的方法进行威胁评估，该方法能够克服传统TOPSIS法在计算权重系数上的不足，但对空战信息的完整性与确定性有很高的要求；文献[3]对传统的威胁评估优势函数进行改进，构造的非参量模型更加合理，但难以保证评估结果的可靠性；文献[4]利用回归型支持向量机方法良好的学习、预测能力来构建空战威胁评估模型，但对于大规模空战训练样本的采集训练则难以实施。上述文献所使用的评估模型的可靠性均需提高，否则很难适用于现代空战。由于空战对抗期间存在着大量的不确定的威胁因素，这些因素都具有随机性、模糊性和不完全性的特点，这就需要寻求一种能够处理含有模糊因子问题的方法。同时运用上述文献中各类方法求出的空战威胁目标属性权重值均是确定的数值，难以体现空战威胁程度的模糊性和不确定性。鉴于以上2点原因，本文提出了基于区间数模糊综合评判法的空战威胁评估模型，综合3种评判函数实现二级综合威胁评估，增强了评估结果的可靠性与说服力。

1 UCAV空战威胁评估模型

UCAV遂行空战任务时，受到的蓝方威胁主要与蓝方战机自身的作战能力和当前的空战态势有关。其中，空战能力可用机动性参数、火力参数、探测能力参数等本机的静态属性量化表示；而空战态势可用角度、距离、速度和高度这4个实时变化的动态因素进行定量分析[5]。

1.1 空战能力威胁

UCAV的空战能力可根据文献[6]中的空战效能指数表示，表达式为

C=[lnB+ln(∑A1+1)+ln(∑A2)]ε1ε2ε3ε4

,

(1)

式中:B为机动性参数；A1为火力参数；A2为探测能力参数；ε1为操纵效能系数；ε2为生存能力系数；ε3为航程系数；ε4为电子对抗能力系数。

对空战效能指数C进行归一化处理，可得空战能力威胁指数为

(2)

1.2 空战态势威胁

利用威胁指数法[7]计算影响空战的4个威胁因素的威胁属性值，假设红方UCAV与蓝方战机进行一对一空战，空战几何关系如图1所示。

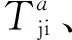
(1) 角度威胁指数为

(3)

(2) 距离威胁指数为

(4)

式中:rji为蓝红双机间的距离;rmi为红方UCAV的最大射程;rmti为蓝方战机的最大射程;rri为红方UCAV的雷达最大跟踪距离。

(3) 速度威胁指数为

(5)

式中:vA为红方UCAV的速度；vT为蓝方战机的速度。

2 区间数方法的相关概念

2.1 区间数特征向量法

(1) 运用特征向量法分别求AL,AU的最大特征值对应的具有正分量的归一化特征向量xL,xU。

(6)

2.2 区间数排序方法[9]

(7)

(8)

3 基于区间数模糊综合评判方法的评估模型

实际空战中，红方UCAV所受到的各方面因素的威胁程度(角度威胁、速度威胁等)均是不易直接量化的指标参数，通常用“极大”、“极小”等定性的评判等级评语进行描述，因此，应用模糊数学理论便可以表示蓝方目标与威胁因素之间的模糊关系，并对各威胁因素进行合理的量化。模糊综合评判法就是应用模糊关系合成的原理，从多个方面(因素)对被评价事物隶属等级状况进行综合性评判的一种方法[10]，该方法具有其他数学模型无法比拟的优势：模型实用、计算简便、能够有效求解多属性决策问题，现已普遍应用于诸多领域。

3.1 模糊综合评判原理

设单因素评判矩阵为R=(rij)m×n，rij∈[0,1]，选择适当的模糊算子，将A与R按照特定的法则运算得到B[11]：

A∘R=B,

式中：“∘”为模糊算子。

3.2 模型的求解

利用上述方法求解此问题模型的步骤如下：

Step 1 确定威胁目标集U={u1,u2,…,um}，集合中的各目标为红方遭遇每架蓝方战机。

Step 2 确定威胁因素集T

根据第1节的分析，这里

T={t1,t2,t3,t4}=
{空战能力指数，角度威胁，距离威胁，速度威胁}。

Step 3 确定模糊关系矩阵R[12]

式中：R为评判矩阵，∀xi,i∈N，行向量(ri1,ri2,…,rim)∈[0,1]m为xi的模糊属性向量，表征蓝方战机xi对威胁因素ti的隶属度。

Step 4 确定评判权重向量A

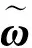
Step 5 计算区间数评判函数F1(R)

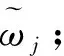
(9)

Step 6 确定模糊综合评判函数φ：[0,1]m→R(R为全体实数集)，记F(·)=φ(z1,z2,…,zm)∈R。这里选取的评判函数，应综合考虑加权隶属度、最大、最小隶属度的综合评判，需要进行二级评判3.3节将对二级评判的具体应用进行分析。

3.3 评判函数的二级评判

本文主要选取下列2种评判函数进行二级评判[13]：

(10)

(11)

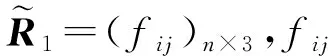
(12)

4 实例分析

本文根据文献[15]中的仿真条件进行实例分析。假设红方出动1架UCAV具有多目标攻击能力，作战过程中发现4架蓝方战机，机型为F-16C，F-5E，F-15E 3种，3种战机的导弹最大射程分别为50,45,55 km，雷达最大探测距离分别为100,200,130 km，且均在红方UCAV火控雷达的探测范围之内，红方UCAV速度vA=32 m/s，携带的中距空空导弹最大射程rmi=60 km，雷达最大跟踪距离rri=120 km。根据相关军事专家对各威胁指标权重的评定意见，构造区间数威胁估计矩阵如表1所示。红方UCAV获取的蓝方战机信息如表2所示。

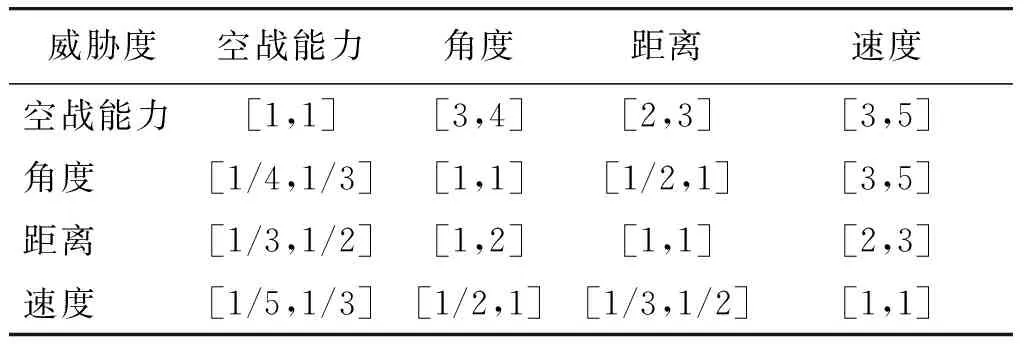
表1 区间数威胁估计矩阵

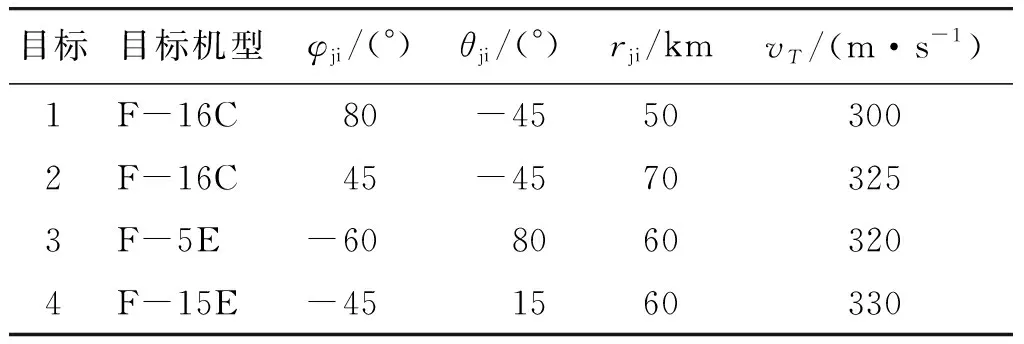
表2 空战态势信息表

利用IEM法对表1中的数据进行计算，得到：

α=0.927,β=1.071,
xL=(0.517 4,0.148 4,0.226 9,0.107 3)T,
xU=(0.491 9,0.160 8,0.233 7,0.113 6)T.

权重向量为

[0.137 5,0.172 1],[0.210 3,0.250 2],

[0.099 5,0.121 6])T.

根据第3节中构建的评估模型得到求解步骤如下：

(1) 该实例中的威胁目标集为

U={F-16C，F-16C，F-5E，F-15E}

.

(2) 确定威胁因素集为

T={空战能力指数，角度威胁，
距离威胁，速度威胁}.

(3) 由式(1)～(5)计算得到模糊关系矩阵为

(4) 由2.2节中的Step 5计算得

T= {[0.569 1,0.643 1],[0.613 6,0.695 1],

[0.324 9,0.372 0],[0.571 1,0.637 2]}.

再根据式(7)得

经式(8)计算后，对结果进行归一化处理，最终算得

F1(R)=(0.267 0,0.345 9,0.125 0,0.262 2).

(5) 利用3.3节中列出的2种评判函数计算Fk(R),k=2,3，计算结果为

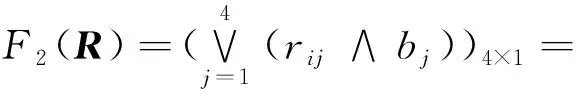
对上述2个结果归一化，结合上一步的计算结果得

(6) 采用二项系数法算出二级评判指标权重ωk=(0.710,0.170,0.120)，对F(R)进行二次评判得

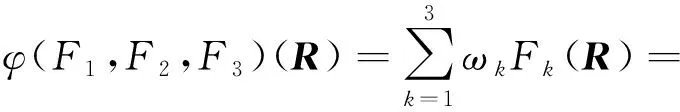
由评判结果可知，最终的威胁排序为X=(2,1,4,3)。该威胁排序结论与文献[15]中的评估结果完全相同，从而验证了本文构建的基于区间数模糊综合评判模型的合理性与适用性。

5 结束语

空战威胁评估是UCAV制定作战计划和进行自主空战战术决策的前提，也是实施协同多目标攻击的关键，对UCAV空战效能的发挥有着举足轻重的影响。本文结合了区间数与模糊综合评判方法的优势，基于上述2种方法构建了空战威胁评估模型。用区间数表示各威胁因素的权重值，并用模糊综合评判方法表征蓝方目标与威胁因素之间的联系，能够有效克服传统方法确定的恒值向量式的威胁权重值无法体现空战威胁程度模糊性、不确定性的不足,也能够弥补确定权重时专家赋值主观性过强的缺陷。最后的实例分析结果与文献[15]中的评估结果相一致，结论在一定程度上能够令人信服。