基于Hypermesh和灵敏度分析的某车型车门轻量化设计

耿少飞，向宇，石梓玉

（广西科技大学汽车与交通学院，广西汽车零部件与整车技术重点实验室，广西 柳州 545006）

引言

车门作为汽车重要开闭件之一，也是使用最为频繁的总成之一，除了外形美观以外，首先要保证车门具有一定的开闭可靠性和足够的刚度性能，刚度不足，会导致开闭件局部区域出现过大变形，影响密封性和安全性，从而影响车辆的正常使用；其次，车门的固有频率与发动机等激励源的激励频率接近时容易发生共振，影响车辆的乘坐舒适性，为此车门更要满足一定的模态性能，所以对车门进行多目标优化具有非常重要的意义。

近年来，近似优化技术由于其高效、实用的特点受到了越来越多的关注。近似优化技术是一种能够通过采用相对较少计算量的数学模型来描述和代替复杂的、高成本的试验或数值模拟[1]，它的最大优点是使优化设计过程的计算时间大大降低。目前比较常用的近似数学模型主要有多项式响应面模型、Kriging模型、径向基函数模型等。国内外各高校企业在这些模型上均已开展了相应的应用研究；朱茂桃等[2]以降低车门质量为目标建立了 Kriging模型进行车门质量优化，在保证车门刚度和模态不变的情况下，使车门达到了轻量化要求；马彬彬等[3]建立了径向基神经网络近似模型，使用模拟退火优化算法对车门进行了轻量化研究，优化效果显著；邢志波等人[4]在进行车门多目标优化中，建立了以模态频率最高和质量最轻为优化目标函数的 Kriging模型，得到了车门部件厚度的最优解；更主要的是Shinkyu Jeong等人[5]还将基于遗传算法的Kriging模型运用到空气动力学设计问题中.另外 J.Forsberg等人[6]在研究汽车结构耐撞性优化时也使用了多项式响应面模型和Kriging模型。

同时，灵敏度分析在汽车的结构优化设计中筛选设计变量时也得到了广泛的应用，郝琪等[7]在对车门结构优化时采用了两种不同的优化方案，基于灵敏度分析方法为设计变量的选取提供了依据，提高了计算效率；朱茂桃等[8]由于车门的一阶、三阶模态频率与白车身固有频率相接近，通过灵敏度分析筛选出关键部件并对其尺寸进行优化，成功避开了车身频率，提高了模态性能；胡启国等[9]对车门进行模态频率优化设计中，选用了基于灵敏度分析的尺寸优化和拓扑优化方法，在达到车门轻量化要求的情况下，模态频率得到了有效地提高。

以上文献大都是在降低车门质量的前提下，只提高了车门模态频率，或者只保证模态和刚度不增加的情况下，进行了车门结构的性能优化，但从改善车门结构的静、动态性能方面，同时进行轻量化设计，目前还未有文章报导。本文将在车门质量极小化的情况下，极力地提高车门低阶模态频率和静态刚度。首先针对各钣金件的厚度对车门性能的影响，通过灵敏度分析方法筛选出影响车门性能的主要部件，将其作为优化设计变量。继而在设计空间内，通过试验设计（des-ign of experiments，DOE）采样构成样本空间并建立多项式响应面数学模型，最后对该数学模型进行车门动静态性能的结构优化。

1 有限元模型建立与分析

1.1 建立有限元模型

车门主要由车门外板、车门内板、外板加强板，外板防撞杆、内板加强板等18个部件组成，各部件均是由薄壁金属冲压而成的钣金件，相互之间通过焊接、粘胶等方式连接形成。考虑到有限元模型的正确性和计算效率，在有限元模型中主要以10mm四边形单元为主，共生成50776个壳单元，其中四边形单元为43112个，三角形单元为7664个，节点数54397个。如图1所示建立了车门有限元模型。

图1 车门有限元分析模型Fig.1 Door finite element model

1.2 有限元模态计算

通过 optistruct求解器，计算有限元模型的约束模态,约束条件分别为在上下铰链处约束 Dx，Dy，Dz，Rx，Ry，Rz，六个方向自由度，在门锁处约束Dx，Dy，Dz，三个方向自由度，并提取其前4阶模态频率，见表1，相应的模态振型如图2（a-d）所示。

表1 车门前四阶计算模态频率值Tab.1 modal frequency value of the first four- order calculation of vehicle door

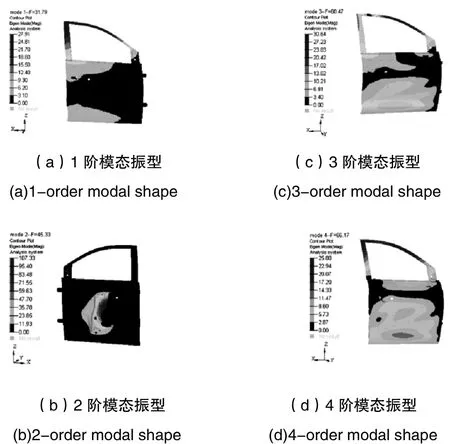
图2 前四阶模态振型Fig.2 Modal shapes of the first four order

1阶固有频率是 31.79Hz，振型表现为车门窗框顶部摆动；2阶固有频率为45.33Hz，振型表现为车门内板局部边缘振动。3阶固有频率是60.47Hz，表现为车门窗框顶部扭转振动。4阶固有频率为66.17Hz，振型表现为车门窗框上部前端、中部以及外板下端的局部扭转振动。

1.3 模态试验及结果对比

为验证有限元模型的正确性，对车门进行模态试验,见如图 3。在车门内外板上分别布置三向加速度传感器，外板布置了21个测点，内板布置了20个测点，以力锤锤击为单点激励，传感器逐点拾取响应信号，将数据采集系统记录下的振动信号保存至计算机，在分析软件内应用频响函数法进行模态计算，得出模态参数。约束模态测试流程图如图4所示，模态测点图如图5所示。最后对比有限元计算模态结果与试验模态结果，见表2。

图3 车门模态试验Fig3 Vehicle door modal test

图4 模态测试流程图Fig4 Flow chart of modal test

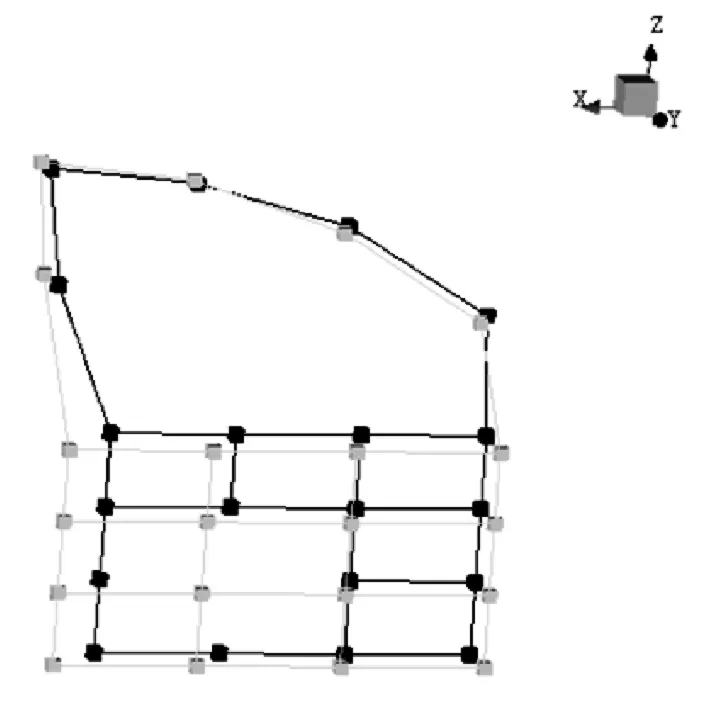
图5 模态试验测点图Fig 5 modal test point map

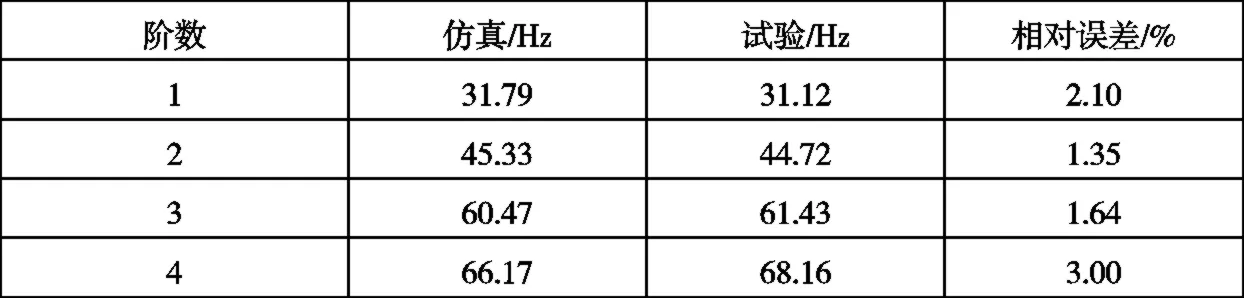
表2 车门前四阶计算模态和试验模态频率值对比Tab2. Comparison of first four order calculation and experimental modal frequency values

由表2对比可知，各阶有限元计算模态频率与试验模态频率相近，振型相似，相对误差均小于 5%，充分说明了有限元模型的正确性。

2 灵敏度分析

2.1 灵敏度分析理论

对于弹性静力学分析，其有限元平衡方程可表示为：

式中，[K]为结构的刚度矩阵，{u}为位移向量，{F}为外部载荷向量。

将式（1）等式两边对结构设计变量xi求偏导数得到：

对于结构的模态分析，无阻尼结构自由振动时的动力学方程为：

式（4）中，[M]为结构质量矩阵，λn为结构第n阶固有频率因子，(为第n阶固有频率)，为第n阶固有振型。

将式（4）等式两边对结构设计变量xi求偏导数得到[10]：

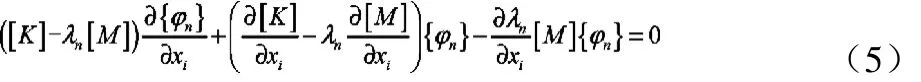
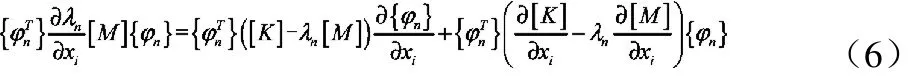
（1）式两边取转置得：

由于刚度矩阵[K]、质量矩阵[M]为对称矩阵，故由（7）式为：

代入(6)式，整理后可得到结构模态频率对设计变量厚度的灵敏度：

2.2 车门部件灵敏度分析

通过灵敏度计算明确结构响应对设计变量的敏感程度，找到主要敏感部件，确定合适的设计变量。在灵敏度分析中以16个主要组成部件的厚度值为设计变量，计算其变化对扭转刚度，下沉刚度及一阶频率的灵敏度。厚度变化可直接表征为质量变化，为衡量部件质量改变对刚度和模态性能的影响，定义以下参考指标[11]：

式（1）中Sm为车门质量对部件厚度变化的灵敏度；St，Sb分别为上、下扭转刚度对部件厚度变化的灵敏度；ST，SB分别为上、下扭转刚度对车门质量变化的相对灵敏度；Ss为下沉刚度对部件厚度变化的灵敏度；Ss为下沉刚度对车门质量变化的相对灵敏度；Sf为一阶模态频率对部件厚度变化的灵敏度；SF为一阶模态频率对车门质量变化的相对灵敏度。

在Hypermesh软件中通过Optistuct求解器计算出车门的上、下扭转刚度、下沉刚度和一阶模态频率，以及质量，对主要部件（1-16）厚度变化的灵敏度，操作流程如图6所示。进而根据式（10）计算出上下扭转刚度、下沉刚度和一阶模态频率对结构质量的相对灵敏度，如表3。

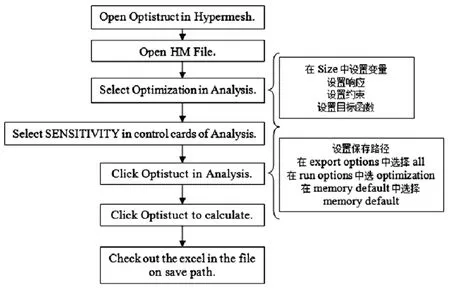
图6 灵敏度分析操作图Fig6 Sensitivity analysis operation diagram

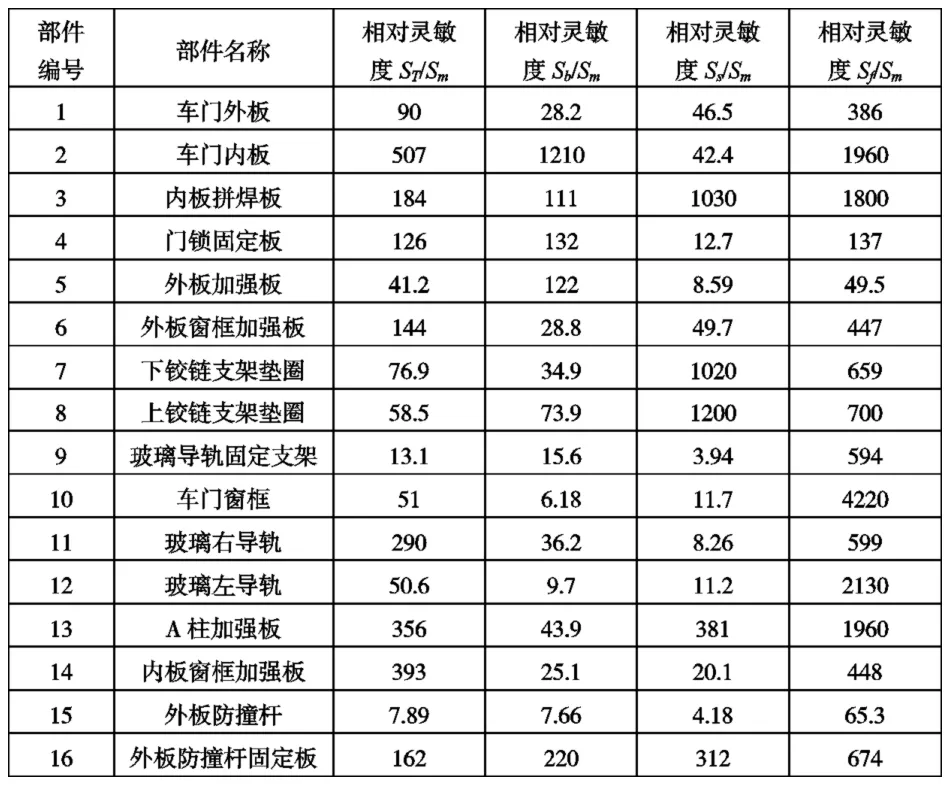
表3 车门部件的相对灵敏度计算Tab3 Relative sensitivity calculation for the parts of door

从表3每列数据中，分别选取两个相对灵敏度较大的所对应的部件和两个相对灵敏度较小的部件。由表可知，共确定出10个相关部件，由于上铰链支架垫圈质量极轻，不做考虑。因此最终确定车门内板、内板拼焊板、玻璃导轨固定支架、车门窗框、玻璃右导轨、玻璃左导轨、内板窗框加强板、外板防撞杆、外板防撞杆固定板9个部件为优化设计对象。

3 车门性能优化

3.1 试验设计

拉丁超立方设计是一种能够随机选取较为均匀的随机抽样方法。与正交试验设计相比，该方法更有能力拟合二阶或更非线性的关系且设计水平值分级比较宽松，试验次数根据实际情况可人为控制。但是拉丁超立方设计仍然存在试验点不均匀的可能，且水平数越多试验点不均匀的可能性越大。基于此缺点，最优拉丁超立方设计方法进行了改进，使得因子和响应的拟合更加精确。

本文基于多学科优化软件Isight采用最优拉丁超立方设计方法进行样本组采样并调用 Optistruct求解器对各组部件物理参数进行有限元分析，得到了各样本组对应的动静态响应值。

3.2 建立近似模型

建立近似模型是一种通过对已知样本点数据进行插值或拟合来建立一个数学模型逼近输入变量与输出变量的方法。通过建立近似模型可以减少工程计算量，在优化过程中能提高优化效率，较快地收敛到全局最优解。

在Isight中建立多项式响应面数学模型时，若多项式阶数较高，则会出现过拟合现象，所以应用较低阶数的多项式。若阶数为2时，根据公式(2)即可求出标准样本组：

式中，P表示样本组数，m表示设计变量个数。经计算，m=9时，P=55。为建立更高精度的数学模型，基于最优拉丁超立方设计，在保证样本组不超过二阶多项式标准样本组的前提下，任意选取了40组样本点。

为了验证该近似模型的精度，再随机生成20组样本点进行误差分析，见表4，复相关系数R2越接近于1表示该数学模型精度越高。由表可知，近似模型各个响应的复相关系数均大于0.9，几乎接近于1。充分说明该近似模型具有较高精度。

表4 车门近似模型误差分析Tab.4 Error analysis of approximate model of door

3.3 多目标优化与结果分析

3.3.1 基于近似模型的多目标优化

基于建立的响应面模型，将车门内板等9个部件的厚度参数作为优化设计变量，以扭转刚度和下沉刚度工况下加载点位移和一阶模态频率为约束，以车门总质量极小化为目标，对车门进行多目标优化。建立的优化数学模型如下：

式中数据均为表 5中的有限元模型响应的初始数值，model为车门一阶固有频率，Dt，Db分别为车门上、下扭转刚度加载点位移，Ds为下沉刚度加载点位移，mass为车门总质量。

9个部件的厚度变化范围、初始值及优化值见表5。

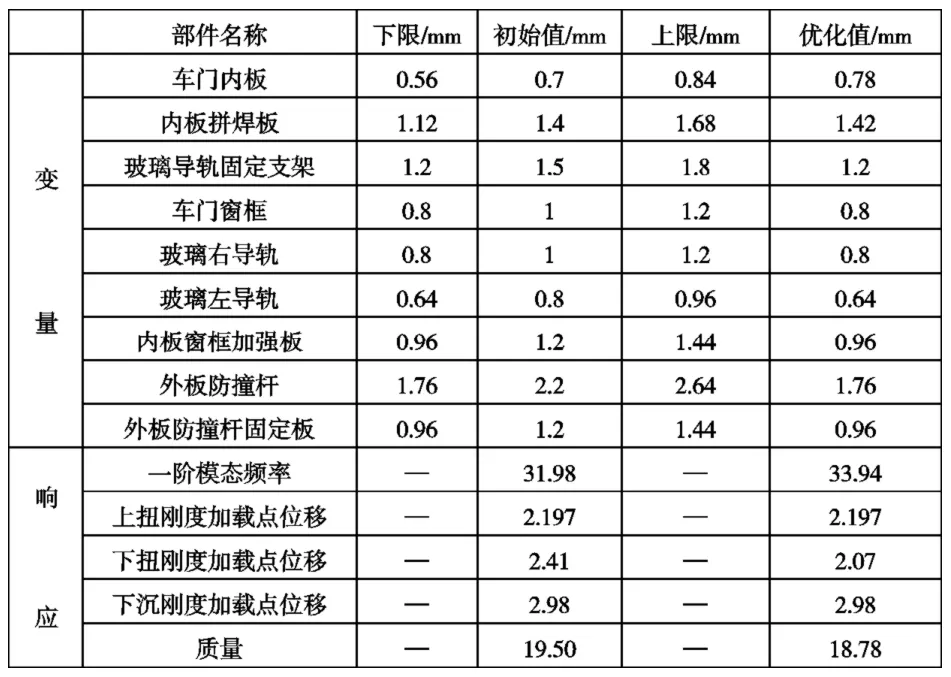
表5 优化变量初始值、上下限和优化值Tab5 Values of initial variables, upper and lower limits and optimization values of optimization variables

由表5可知，除车门内板和内板拼焊板厚度变大外，其余部件厚度均变小。车门总质量在有效降低3.69%的情况下，一阶模态频率增大了 6.13%，下扭刚度加载点位移减小了14.11%，上扭刚度加载点位移和下沉刚度加载点位移均未有变化。

4 结论

文中在对车门结构进行多目标优化时，根据对结构性能参数的具体要求确定目标函数与性能约束，在车门质量降低的情况下，一阶模态频率增大了 6.13%，上扭刚度加载点位移未改进，下扭刚度加载点位移减小了14.11%，下沉刚度加载点位移未改变。总之，在对某车型车门进行轻量化设计中，不仅使车门总质量得到降低，其下扭刚度也得到了提高，抵抗变形的能力得到了加强，车门的密封性也得到了改善，更好得保证了车内乘员的安全性，同时车门低阶模态得到提高，有效地避开了来自于发动机怠速和路面的低频激励，提高了乘员的舒适性。