汽车非线性悬架系统振动分析

成 洁

（武警后勤学院，天津 300309）

前言

军用汽车使用环境复杂，运行条件恶劣，经常行驶在凹凸不平的路面或复杂环境中，对悬架的减振性能有较高要求。以往对军用汽车平顺性的研究，多建立线性模型对悬架振动进行分析，实际上军用汽车悬架多采用具有干摩擦效应的钢板弹簧或变刚度螺旋弹簧，具有明显的非线性特性。高性能的控制器设计必须以建立精确的悬架振动模型为基础。因此，针对军用汽车悬架系统，应建立更符合实际工况的悬架非线性振动模型，分析其平顺性能，对设计悬架系统、研发高效的振动控制器具有重要作用。

系统的非线性振动问题通常用非线性微分方程来描述，解析法是求解非线性微分方程定量分析法中最基本的分析方法，包括FPK法、频闪法、小参数法、渐进法、谐波平衡法、统计线性化方法等。

统计线性化方法适合在系统具有弱的非线性的条件下使用。研究表明，悬架系统具有弱的非线性且多处响应都是平稳正态或接近正态分布的随机过程，其时间历程近似于窄带随机过程[1]，因此本文采用统计线性化方法求解。统计线性化方法是非线性确定性振动的等价线性化方法推广到随机振动领域的一种近似方法，基本思想是将非线性振动系统进行等效线性化处理[2]，然后求解等效线性化方程，该方法于1959年由Caughey研究提出。本文模拟了对军用汽车形成较大冲击的凸起或凹坑路面，建立了车辆后悬架两自由度非线性振动模型，利用统计线性化方法对悬架非线性振动时域响应进行分析，并借助 MATLAB/Simulink软件模拟了悬架的性能指标输出曲线。

1 悬架系统非线性振动模型

1.1 变刚度螺旋弹簧的刚度特性

军用汽车前悬架多采用特性线为非线性的变刚度螺旋弹簧。常见的变刚度螺旋弹簧分为变节距螺旋弹簧、变截面螺旋弹簧和变径螺旋弹簧三种。变径螺旋弹簧包括蝶形螺旋弹簧和塔形（圆锥）螺旋弹簧，具有较大的横向稳定性。以塔形螺旋弹簧为例说明其刚度特性。图1为截锥螺旋弹簧剖面图极其刚度特性曲线[3]。弹簧受到初始载荷后，特性线 OA段为是直线；当载荷逐渐增大时，弹簧从大圈一端开始压缩，各段逐渐接触，有效工作圈数减少，刚度则逐渐增大，直到所有弹簧圈完全压并为止结束，特性线AB段为上升形曲线。因为曲线各点的切线斜率不断增大，载荷与变形关系为非线性，其自振频率为变值，能有效防止发生共振，因此广泛应用于车辆悬挂装置。本文研究的军用汽车前悬架采用圆锥形变刚度螺旋弹簧。

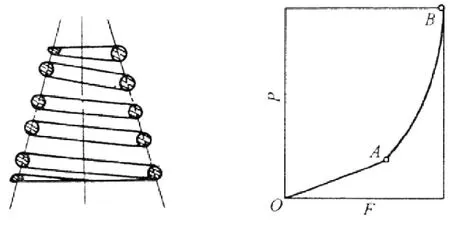
图1 截锥螺旋弹簧极其特性曲线

如前所述，汽车中存在许多非线性因素，这里只考虑悬架弹簧的非线性刚度特性。

变刚度弹簧的回复力-位移关系可表示为：

式中Fs为弹簧回复力，k为弹簧刚度，x为弹簧位移，ε为一表示弹簧非线性程度的小参数，ε=0时，该弹簧为线性。其力-位移关系曲线如图2所示，虚线代表线性弹簧的回复力-位移曲线，实线代表非线性弹簧的回复力-位移曲线。

汽车是一个非常复杂的非线性多自由度系统，以研究汽车垂直振动为目的建立描述汽车运动特性的数学模型，可采用1/4车体模型。

1.2 两自由度悬架系统非线性振动模型

图 3为悬架系统的力学模型。其中 m2为簧载质量，m1为非簧载质量，k1为轮胎刚度，c2为减振器粘性阻尼系数，z2为簧载质心垂直位移，z1为非簧载质心垂直位移，z0为路面不平激励，F(z2-z1)为非线性弹性力。系统的运动微分方程为：

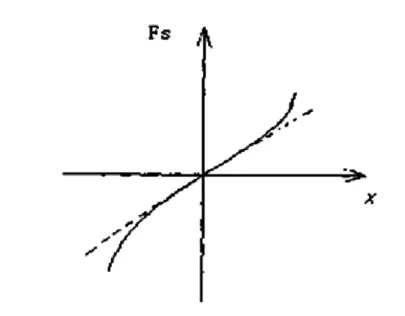
图2 变刚度弹簧力—位移曲线

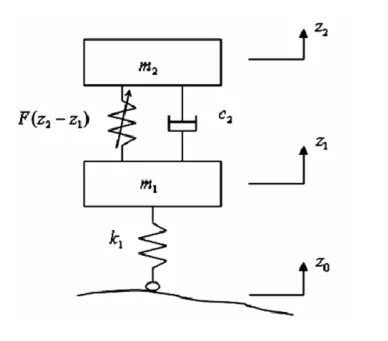
图3 两自由度悬架振动模型

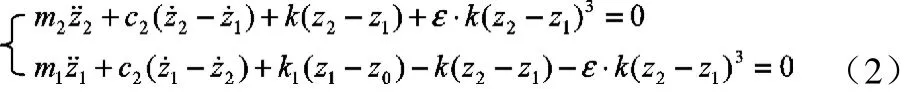
2 用统计线性化方法求解汽车非线性振动问题

统计线性化方法的基本思想[2]，是以线性函数等效地替代非线性函数，使得非线性随机微分方程按照统计意义上误差最小的原则变为形式上是线性的随机微分方程，然后按照线性随机振动理论处理，得到响应的时域信息（均值和均方值）。

将方程（2）写成矩阵形式

式中

作坐标变换

A(1)，A(2)分别为系统的两个主振型，D1，D2是正则化因子。方程解耦后，原方程组转化为两相互独立单自由度系统方程。令（i=1,2,3）为待定系数。根据统计线性化方法

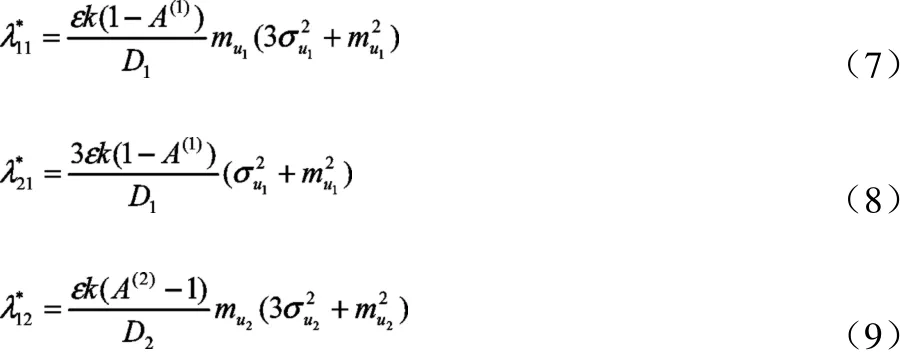
因此方程（5）经线性化后变为

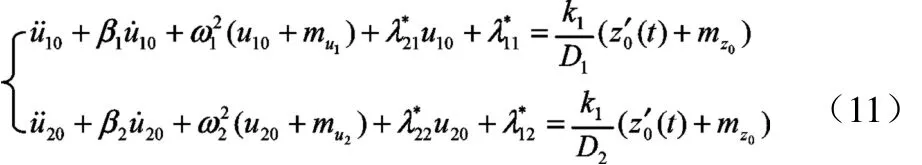
3 冲击路面不平度的模拟

汽车在行驶过程中会遇到凸起或凹坑，对悬架可形成较大冲击。本文拟采用半波正弦信号近似模拟凸起路障的冲击信号。利用MATLAB/SIMULINK软件对路面不平度进行仿真，得到如图4所示的凸起路障的时域模拟信号。

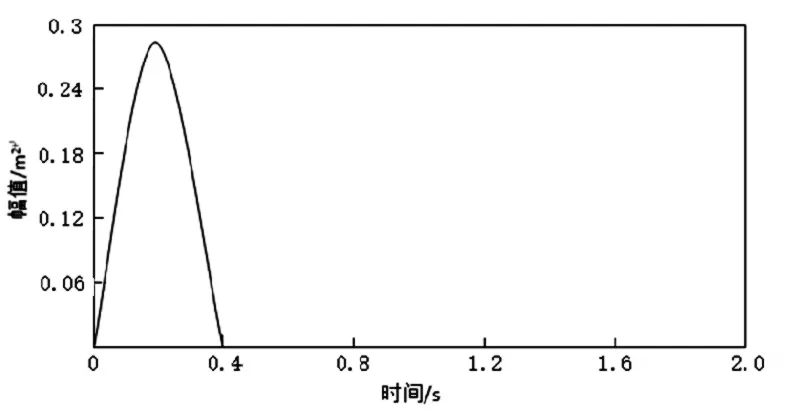
图4 凸起路障的模拟冲击信号

4 悬架系统仿真模型的建立

为了便于分析模型的非线性振动特性，用 MATLAB/Simulink工具箱分别对线性悬架系统模型和非线性悬架系统模型进行仿真，并对仿真结果进行对比。仿真模块图见图5、图6。

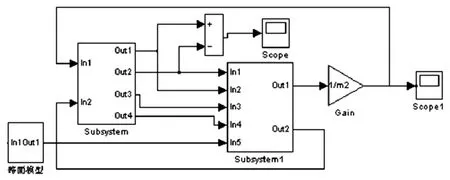
图5 线性悬架系统模型

图6 非线性悬架系统模型

5 计算结果及在MATLAB上的仿真实现

某型汽车的相关计算参数为：m2=1231.49kg，m1=173.61 kg，c2=3146Ns/m，k=95789N/m，k2=1283673N/m，取ε=0.15。

系统仿真输出变量为：车身垂直振动加速度、车轮动位移、悬架动扰度，这是衡量汽车平顺性和安全性的重要参数。图7～图10分别为线性悬架系统和非线性悬架系统的时域输出响应曲线。

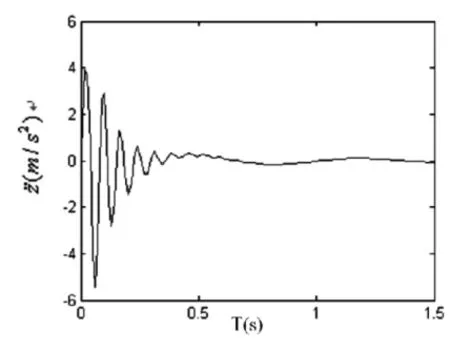
图7 线性悬架系统车身加速度

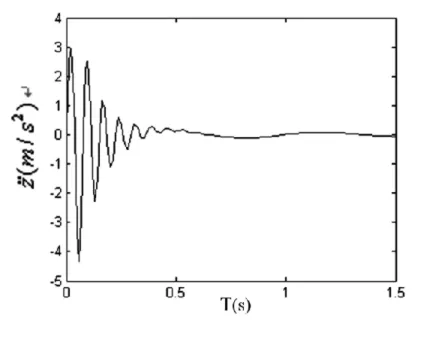
图8 非线性悬架系统车身加速度

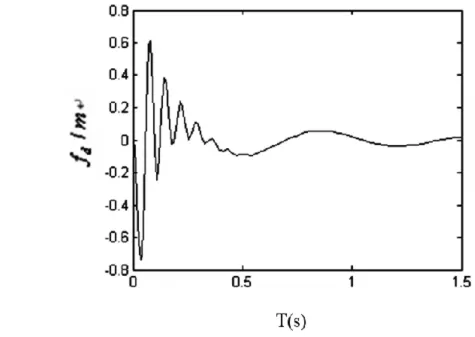
图9 线性悬架系统车身动挠度

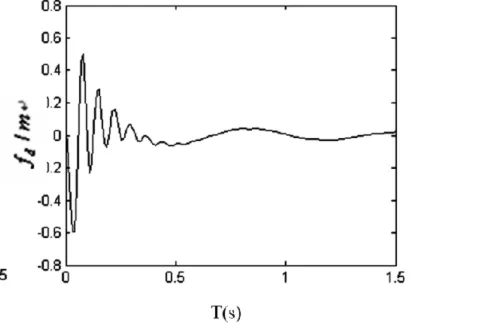
图10 非线性悬架系统车身动挠度

表1 不同悬架模型仿真结果比较

从以上仿真结果可以看出，当路面激励为凸起型路障时，非线性悬架的车身加速度和悬架动挠度的峰值和均方根值都小于线性悬架，说明非线性悬架的控制性能优于线性悬架且更接近实际控制情况。

6 结论

本文以凸起型路障作为路面激励,分析了非线性弹簧的刚度特性，建立了基于变刚度螺旋弹簧的两自由度汽车悬架系统非线性振动模型，采用统计线性化方法，借助线性随机振动理论，求解了悬架系统非线性振动问题，并利用MATLAB软件对该模型进行了动力学仿真，仿真结果输出了各物理量在时域内的变化曲线。仿真结果表明：悬架的非线性特性不容忽视，利用统计线性化方法求解汽车悬架系统的非线性振动问题是可行而且可靠的，硬特性非线性悬架的减振效果优于线性悬架，可根据仿真结果从而判断汽车的平顺性。