简约而不简单:由线性函数及其图像说开去


摘 要:线性函数是最基本、最简单的函数,其函数图像是一条倾斜的直线,具有简洁美、抽象美。线性函数及其图像在物理学上有着廣泛的应用,既可以通过直线的斜率与直线下方的面积求有关物理量,又可以根据图像的直观性简洁地分析有关问题,还可以通过巧设坐标系中的物理量,将非线性函数图像转化为线性函数图像,形象地描述物理量之间的变化规律。挖掘线性函数及其图像应用中所蕴藏的物理思想,简洁而又深邃,简约而不简单。
关键词:线性函数;线性函数图像;正比例函数;一次函数;图像转化
中图分类号:G633.7 文献标识码:A 文章编号:1003-6148(2018)10-0060-4
物理学既是实验科学,又是一门高度数学化的自然科学。物理定律的简洁性,体现在基本定律的数学形式尽可能简单,基本定律的数学方程尽可能少。在物理学发展史上的很长一段时间内,寻找“线性”与追求“平衡”一样,曾被人们看作是“完美”的、理想的追求目标[1]。线性是一个很宽泛的数学或物理概念,在不同的情况下有不同的内涵。例如,线性函数、线性方程(组)、线性代数、线性空间、线性变换等。本文探讨线性函数及其图像在物理学上的应用。
1 线性函数概述
形如y=f(x)=kx+b(k≠0,k、b是常数)的解析式表示的函数叫线性函数,也叫一次函数。在平面直角坐标系中,线性函数的图像是一条直线,其定义域是整个实数。当k>0时它是递增函数(图1所示);当k<0时它是递减函数(图2所示)[2]。式中, k、 b分别对应直线的斜率和截距。b=0的函数为正比例函数,它是一次函数的特例。
若两个变量之间存在线性函数关系,则称它们之间存在线性关系。正比例关系是线性关系中的特例,反比例关系则不是线性关系。
根据物理学的特点和问题分析的习惯,本文将线性函数划分为2个层级,即正比例函数与一次函数。
2 正比例函数及其图像在物理学上的应用
在中学物理中,有许多物理量之间的关系遵循着正比例函数关系。例如,初速度为零的匀加速直线运动的速度与时间成正比;在弹性限度内,弹簧的弹性力与形变量成正比;电容器所带的电荷量与两板间电势差成正比等[3]。
在正比例函数图像中,直线的斜率及其下方的面积往往对应一个物理量。例如,速度-时间图像中,直线的斜率表示加速度,直线下方的面积表示一段时间内质点的位移。
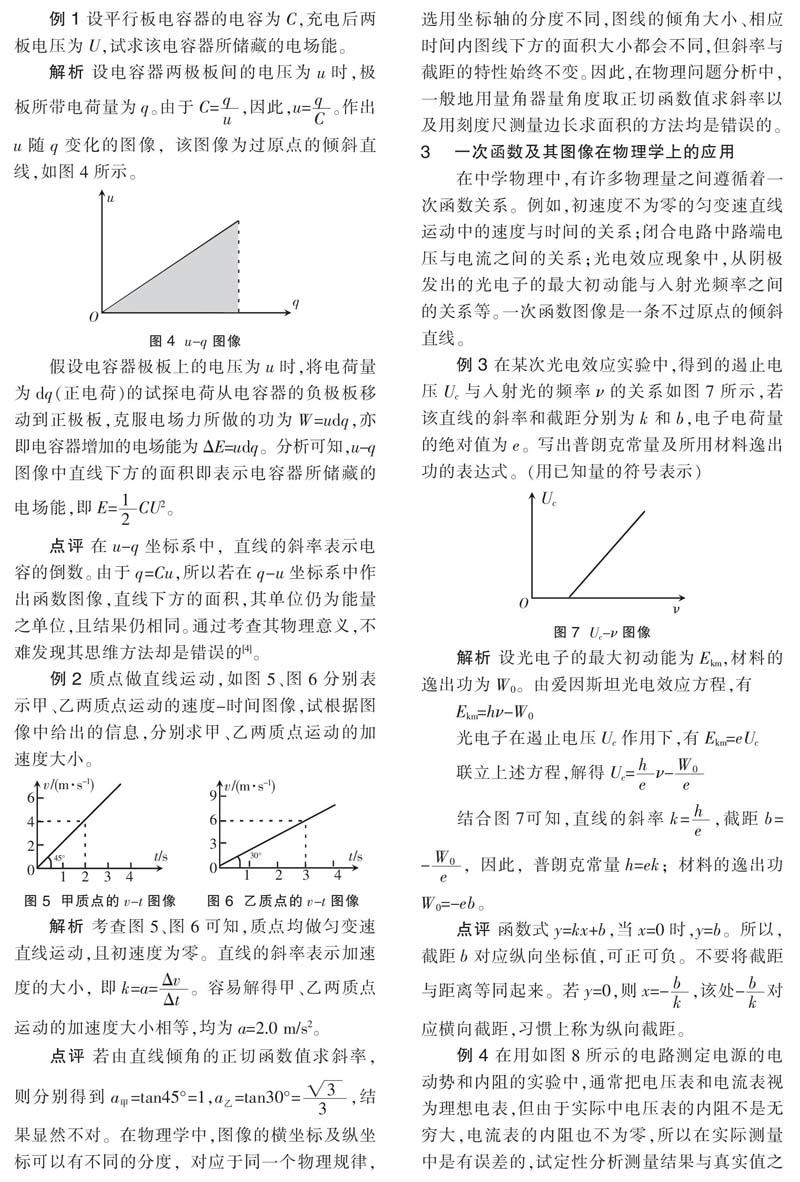
例1 设平行板电容器的电容为C,充电后两板电压为U,试求该电容器所储藏的电场能。
点评 在u-q坐标系中,直线的斜率表示电容的倒数。由于q=Cu,所以若在q-u坐标系中作出函数图像,直线下方的面积,其单位仍为能量之单位,且结果仍相同。通过考查其物理意义,不难发现其思维方法却是错误的[4]。
例2 质点做直线运动,如图5、图6分别表示甲、乙两质点运动的速度-时间图像,试根据图像中给出的信息,分别求甲、乙两质点运动的加速度大小。
3 一次函数及其图像在物理学上的应用
在中学物理中,有许多物理量之间遵循着一次函数关系。例如,初速度不为零的匀变速直线运动中的速度与时间的关系;闭合电路中路端电压与电流之间的关系;光电效应现象中,从阴极发出的光电子的最大初动能与入射光频率之间的关系等。一次函数图像是一条不过原点的倾斜直线。
例3 在某次光电效应实验中,得到的遏止电压Uc与入射光的频率ν的关系如图7所示,若该直线的斜率和截距分别为k和b,电子电荷量的绝对值为e。写出普朗克常量及所用材料逸出功的表达式。(用已知量的符号表示)
例4 在用如图8所示的电路测定电源的电动势和内阻的实验中,通常把电压表和电流表视为理想电表,但由于实际中电压表的内阻不是无穷大,电流表的内阻也不为零,所以在实际测量中是有误差的,试定性分析测量结果与真实值之间的误差[5]。
解析 在实验设计中,我们把电流表及电压表看成理想表。先测出多组电压、电流值,然后根据电压、电流值作出U-I图像,如图9中的实线所示。根据“外推法”求出电源的电动势和内阻。由于两电表内阻是客观存在的,所以在测量中不可避免地会产生误差。
4 非线性函数图像转化为线性函数图像
线性函数图像是一条直线,直线是最简洁的图像。莎士比亚说,简洁是智慧的灵魂。简洁之美,在物理美中占有极其重要的位置。杨振宁指出:“一粒沙子有一个世界,一朵花里有一个天堂”,富有哲理的两句名言,来概括物理的简洁之美,是很准确而又形象生动的[6]。
直线,无头无尾,承前启后,给人以无限的遐想;在平面直角坐标系中,一条倾斜直线穿过坐标系,不偏不倚,心无旁骛,彰显了简洁美与抽象美。
例5 利用图10所示的装置可测量滑块在斜面上运动的加速度。一斜面上安装有两个光电门,其中光电门乙固定在斜面上靠近底端处,光电门甲的位置可移动。当一带有遮光片的滑块自斜面上滑下时,与两个光电门都相连的计时器可以显示出遮光片从光电门甲至乙所用的时间t。改变光电门甲的位置进行多次测量,每次都使滑块从同一点由静止开始下滑,并用米尺测量甲、乙之间的距离x,记下相应的t值;所得数据如表1所示。
(1)若滑块所受摩擦力为一常量。试写出滑块加速度的大小a、滑块经过光电门乙时的瞬时速度v、测量值x和t四个物理量之间所满足的关系式;
(2)根据表中给出的数据,合理选择横轴及纵轴所表示的物理量,建立平面直角坐标系,作出相关图像,要求图像中的图线呈现为直线;
(3)根据所画图像求出滑块加速度的大小。(保留2位有效数字)
著名数学家G·波利亚建议将古代哲学家们所说的“简洁是真理的标记”,改成另一种说法“先从最简单的试起”。他认为:“由于人类已经具有了几个世纪的悠久而丰富的大量科学经验,所以现在表达起来应该更慎重一些;我们知道真理可能是非常复杂的。”[7]基于此,从认识论的视角来考量,面对错综复杂的自然界,从建立线性函数关系开始或从求解线性运动方程入手的处理方法对于人们认识世界是十分必要的,也是认识客观世界的一条行之有效的简化途径[1]。对于物理量之间存在的非线性函数关系,人们总是试图用线性函数关系进行近似、转化或简化处理。可以说线性函数及其图像的简洁性、直观性,带给我们的是一种“美”。透视线性函数及其图像应用中所蕴藏的物理思想,可以概括为:简洁而又深邃,简约而不简单。
参考文献:
[1]朱鋐雄.物理学方法概论[M].北京:清华大学出版社,2008:176.
[2]张顺燕.数学的思想、方法和应用(修订版)[M].北京:北京大学出版社,1997:139.
[3]王溢然,王亮.中学物理思维方法丛书·图示与图像[M].郑州:大象出版社,1999:69-70.
[4]许冬保.剖析应用图像面积求物理量时的一个隐蔽性错误[J].中学物理教学参考,2014,43(11):26-27.
[5]宓子宏.高中物理系统训练指南[M].上海:上海辞书出版社,1998:488-489.
[6]祝娅.物理发现中的哲学和创造性思维[M].北京:知识产权出版社,2011:213.
[7]刘佑昌.现代物理思想渊源(修订版)[M].北京:清华大学出版社,2010:297.

