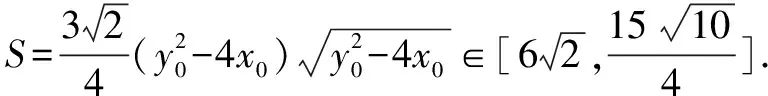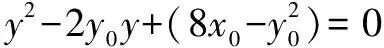2018浙江高考理科21解法探究

许银伙

(福建省泉州外国语中学 362000)

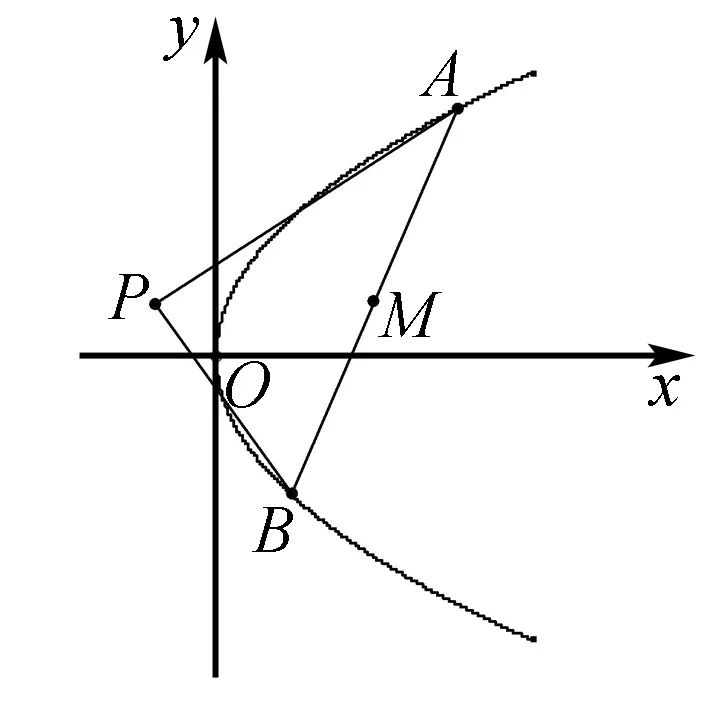
问题 (2018年浙江高考理科21)如图，已知点P是y轴左侧(不含y轴)一点，抛物线C：y2=4x上存在不同的两点A，B满足PA，PB的中点均在C上.

(1)设AB中点为M，证明：PM垂直于y轴；

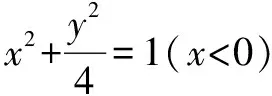
入手一 设出直线AP，BP斜率k1,k2和P,A,B坐标，然后利用中点公式，韦达定理，弦长公式，点到直线距离公式，面积公式等知识解题.

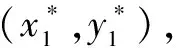
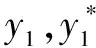
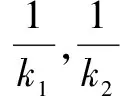
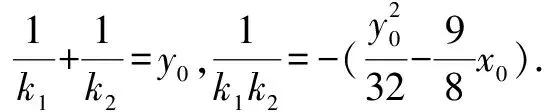
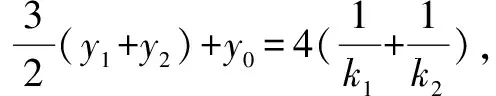
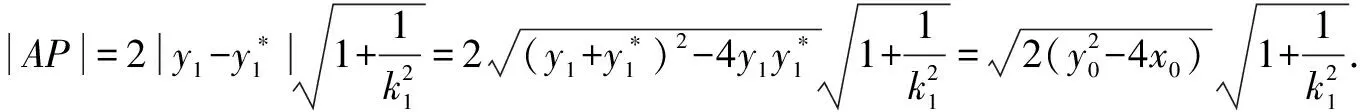
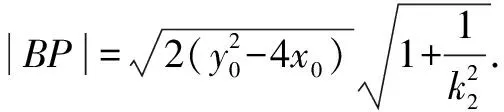
设∠APM=α,∠BPM=β，

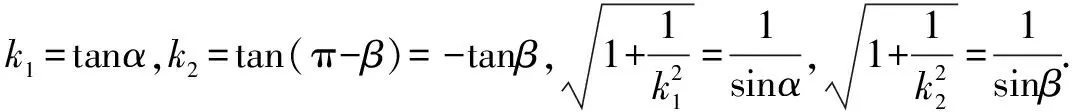
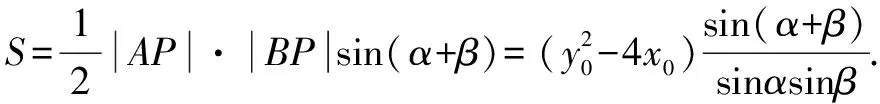
思路二 设直线AB的斜截式方程和P,A,B坐标，然后利用中点公式，韦达定理，弦长公式，点到直线距离公式，面积公式等知识解题.

方法二 (1)证明：设点P(x0,y0),A(x1,y1),B(x2,y2)，

①直线AB斜率存在时，设方程为：y=kx+b，代入y2=4x得：k2x2+2(kb-2)x+b2=0，

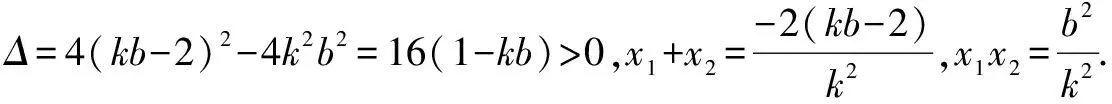
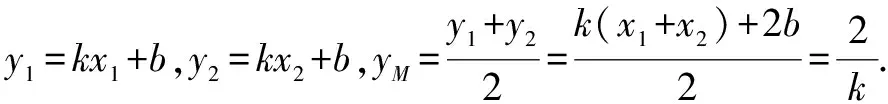
同理得：

所以x1,x2是方程k2x2+2[(y0+b)k-4]x+(y0+b)2-8x0=0的两个不同的实数根，

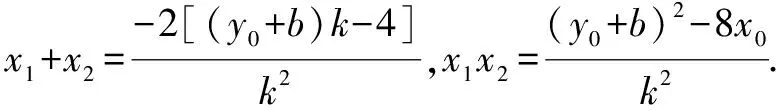
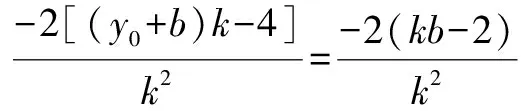
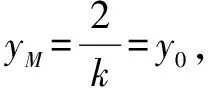
②当直线AB斜率不存在时，由抛物线性质得PM垂直于y轴必成立.

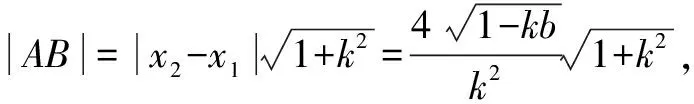
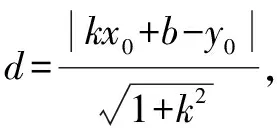
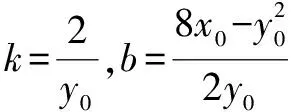
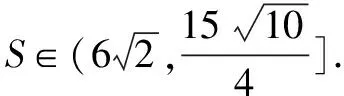
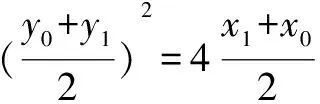
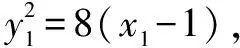
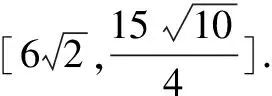
思路三 利用直线AB斜率必不等于零，且允许斜率不存在，设直线AB的倒斜式方程和P,A,B坐标，然后利用中点公式，韦达定理，弦长公式，点到直线距离公式，面积公式等知识解题.

方法三 (1)证明：设点P(x0,y0),A(x1,y1),B(x2,y2)，由已知可设直线AB方程为：x=t+my，

代入y2=4x得：y2-4my-4t=0，判别式Δ=16(m2+t)>0，y1+y2=4m,y1y2=-4t.

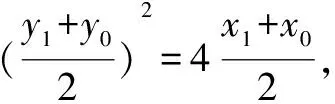
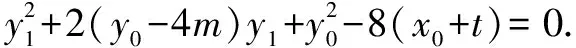
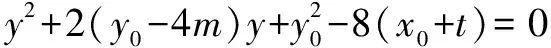
又由韦达定理得：

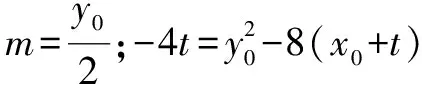
∴yM=y0，则PM垂直于y轴成立.

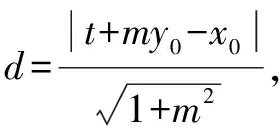
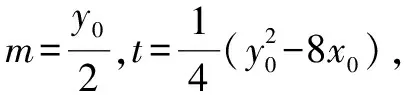
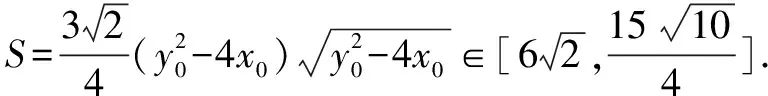
思路四 利用点A,B在抛物线上和第一步要证明的结论，由纵坐标设点A,B坐标，然后利用中点公式，弦长公式，面积公式等知识解题.

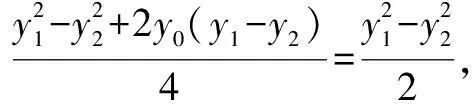
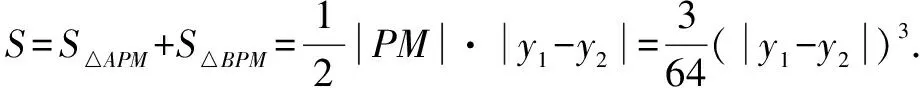
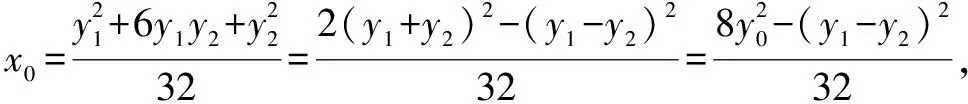
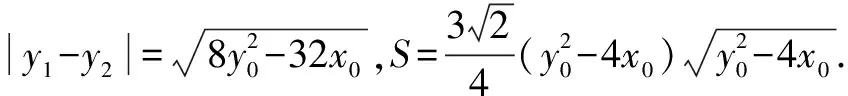
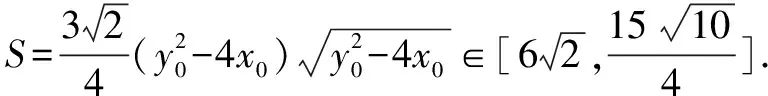
思路五 利用点A,B在抛物线上和第一步要证明的结论，由纵坐标设点A,B坐标，然后利用中点公式，韦达定理，弦长公式，面积公式等知识解题.

方法五 (1)证明：接方法四，由

整理得：

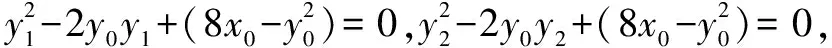
(2)解：

由(1)得：

△PAB面积

同方法一得：