算两直线交点坐标解圆锥曲线解答题
2018-12-27 08:30李宁
数理化解题研究 2018年34期
李 宁
(海南省海南中学 571158)
在圆锥曲线解答题中,有时候需要算出两直线的交点坐标来参与下一步的求解. 而此时的直线往往是动直线,直线方程含有参数,算出来的交点坐标往往结构比较复杂. 为了能够顺利算出交点坐标,可向学生介绍解线性方程组的克莱姆法则.
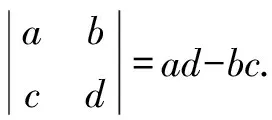
(1)求椭圆C的方程;
(2)已知A为椭圆的左顶点,过椭圆C内一点M(1,0)作斜率为k1的直线l与椭圆C交于P,Q两点,若点N为△APQ的外心,直线ON的斜率为k2,求证:k1·k2为定值.
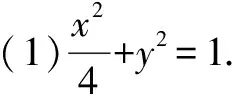
(2)设P(x1,y1),Q(x2,y2),直线l:x=my+1,代入x2+4y2=4,
整理得:(m2+4)y2+2my-3=0,
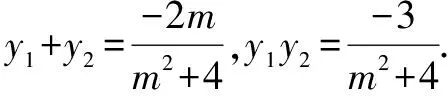
又A(-2,0),则AP的中垂线方程为(x+2)2+y2=(x-x1)2+(y-y1)2,
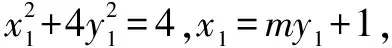
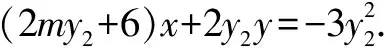
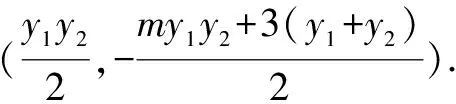
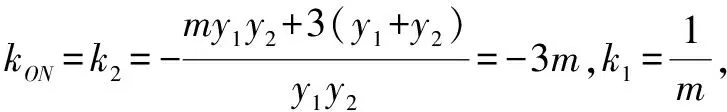
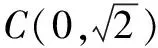
(1)求椭圆的方程;
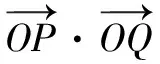
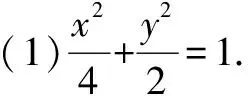
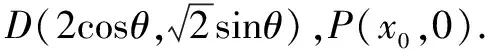
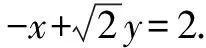
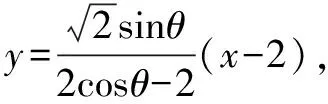
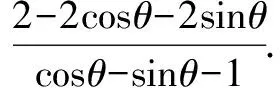
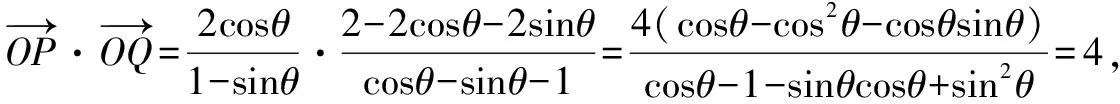
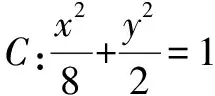
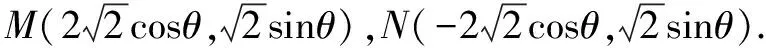
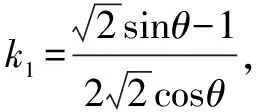
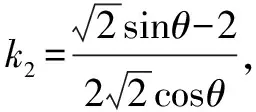
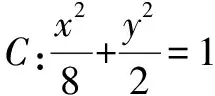
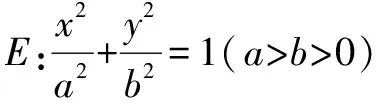
(1)求a,b的值;
(2)求证:直线MN的斜率为定值.
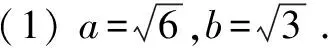
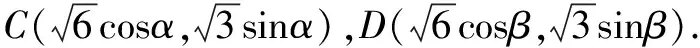
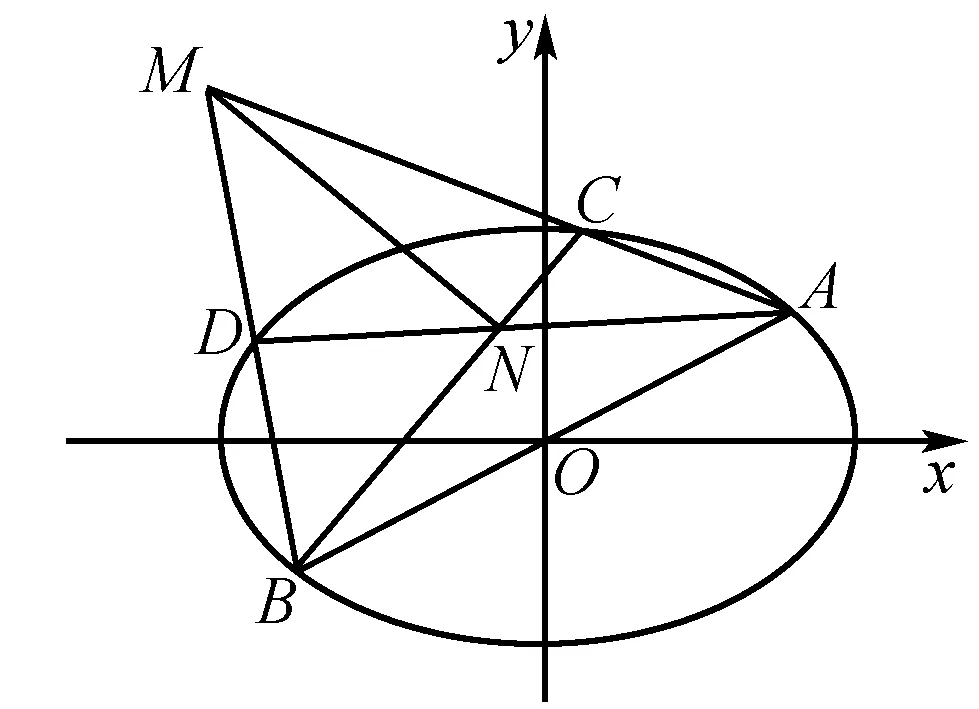
①假设AC,BD,AD,BC四条直线的斜率均存在.
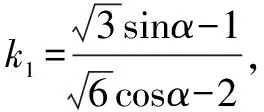
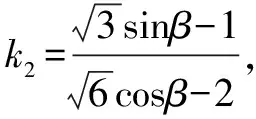
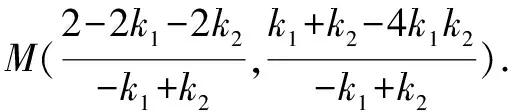
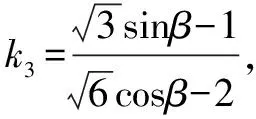
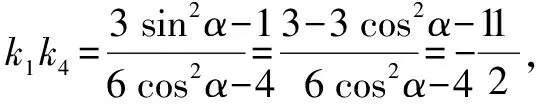
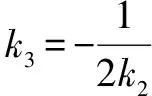
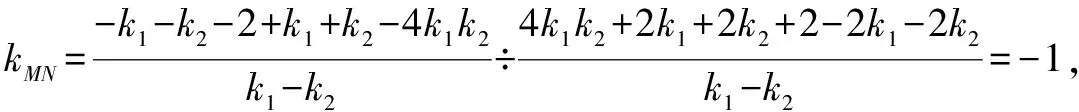
②若AC,BD,AD,BC四条直线中有直线斜率不存在,由题意此时只能有一条直线斜率不存在.
不妨设直线BD斜率不存在,此时D(-2,1),直线AC:y-1=k1(x-2).
令x=-2,解得此时M点坐标(-2,1-4k1).
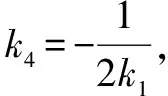

综上所述,直线MN的斜率为定值.
如果直线斜率结构比较复杂,可先不急着将斜率的内容代入直线,而是挂着斜率k算出交点坐标,然后再将斜率具体的内容代入坐标化简.
猜你喜欢
小学生学习指导(高年级)(2022年10期)2022-11-04
中学生数理化(高中版.高二数学)(2022年1期)2022-04-26
新世纪智能(教师)(2021年2期)2021-11-05
学生导报·东方少年(2019年7期)2019-06-11
电子制作(2018年10期)2018-08-04
电子制作(2018年12期)2018-08-01
中学生数理化·七年级数学人教版(2017年3期)2018-01-20
数学学习与研究(2017年11期)2017-06-20
青年时代(2017年3期)2017-02-17
中学生数理化·七年级数学人教版(2017年12期)2017-02-15

