一种基于差分进化的教与学优化算法

刘 印，李 丹

（东北大学秦皇岛分校，河北 秦皇岛 066000）

教与学优化算法是印度学者Rao等在2011年提出的一种算法，是现代元启发式算法之一。它的原理是通过模拟传统的课堂教学中老师对学生的教授，以及学生自己的自学这两个过程，来达到寻优的目的[1]。自算法提出就获得了世界各地的学者关注，并被考虑作为解决复杂优化问题的最优算法之一。自算法提出以来，被用于多个领域。例如，Rao等用教与学算法来优化无约束函数和约束函数。华洁等[2]用教与学算法对沼气的液化换热器结构进行了优化。何红等[3]利用改进的教与学算法对旅游线路进行了优化。To等用教与学算法对平面钢框架的设计进行了优化。Basu等用教与学算法处理多区域的经济负荷分配问题。拓守恒等[4]使用教与学优化算法对神经网络中的权值和阀值进行了一定优化。

1 教与学优化算法

1.1 初始化

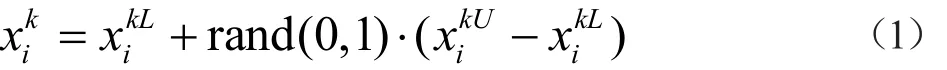
1.2 教学阶段

学生根据教师Xteacher和学生的平均值Xmean之间的差异进行学习：

1.3 学习阶段

学生之间可以通过互动来提高他们的水平：

在“教学阶段”和“学习阶段”完成之后，执行贪婪选择策略决定是否更新适应度和学生的成绩。

2 基于差分进化的教与学优化算法

2.1 自适应教学因子

在教学过程的前期，因为老师和学生之间的差距很大，且学生对于要学习的知识比较陌生，所以学生的学习效率较高，学习知识快。而在经历了一段时间的学习后，学生所掌握的知识逐渐增多，与老师的差距渐渐缩小，学习的效率逐渐下降。为了解决此问题，引入自适应教学因子：

其中，TFmin为教学因子最小值；TFmax为教学因子最大值；tmax是最大迭代次数；ti是当前迭代次数。

2.2 基于差分进化的修正学习阶段

在学习阶段引入基于差分进化思想的多样化学习方法。当选择的学生Xj优于学生Xi时，期望学生Xi接近更好的学生Xj以提高解决方案的质量。同时，学生的互相学习也受到老师的指导，学生和老师的水平相差越大，受到的影响也越大。

当所选择的学生Xj比学生Xi差时，随机从班级选出另外两个学生Xr1和Xr2，借鉴DE交叉和选择环节生成Xinew。

CR为DE中的交叉因子。这种改进不仅在学习阶段中合理控制老师的影响，还使更多的学生参与到了当前学生的学习过程，提高了种群的多样性。

3 实验分析

为对本文算法性能进行评价，本节选取9个具有不同属性的测试函数进行评估，并与5种改进的教与学优化算法（Teaching Learning Based Optimization，TLBO）算法比较。其中F1-F4单峰函数，而F5-F9是多峰函数。所有测试函数在D=30的维度上进行测试。种群数量NP设置为40，迭代次数为1 000，每个函数独立测试30次。

图1显示了几种算法在9个测试函数上的迭代曲线，其中，t为迭代次数，纵坐标F为适应度函数值。为方便观察将其取log值，曲线越靠近下方则代表收敛性能越优秀。

图1显示本文所提出的算法整体效果上表现最优，兼顾了收敛速度和收敛精度，在所有测试函数上的表现均比较优异，虽然算法的运行时间有一定的增加，但这是可以接受的。总的来说，DITLBO算法的改进是成功的，很大程度上提高了TLBO算法的综合能力。

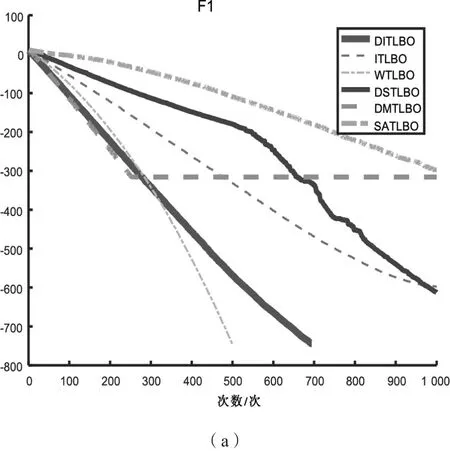
图1 几种算法的收敛曲线比较

4 结语

本文提出了一种基于差分进化的自适应教与学优化算法。针对高维复杂优化问题中容易陷入局部最优的不足，采用自适应教学因素和基于差分进化的学生阶段来提高基本的TLBO。对CEC的9个复杂测试函数进行了实验分析，证明了该方法的有效性。所提出的方法能够有效地为这些复杂的测试函数提供稳定和高质量的解。未来的研究工作将进一步提高算法能力，并尝试将其应用于解决一些实际问题。