常见几何体的表面展开图

◎王长颖

（作者单位：南京市第一中学江北新区学校）

研究立体图形的时候，我们可以通过研究平面图形（如三视图）的性质来研究几何体的性质.几何体转化为平面图形还有一种方法，那就是将几何体的表面展开，得到平面图形.我们可以通过研究立体图形的表面展开图来研究立体图形的性质，但并不是所有几何体的表面都可以展开成平面，如球的表面就不能展开成平面.这里我们列举几种常见立体图形的表面展开图供同学们学习.

一、常见几何体的展开图

1.圆柱的表面展开图.

圆柱的表面展开图由两个大小完全一样的圆（底面）和一个长方形（侧面）组成，如图1.

图1

友情提醒：圆柱展开图得到的两个圆的周长和长方形的一边长相等，长方形的另一边的长等于原来圆柱的高.

2.圆台的表面展开图.

圆台的表面展开图由大小不同的两个圆（底面）和扇形的一部分（侧面）组成，如图2.

图2

友情提醒：展开后的两个圆的周长分别等于两段弧的长度.

3.圆锥的表面展开图.

圆锥的表面展开图由一个圆（底面）和一个扇形（侧面）组成，如图3.

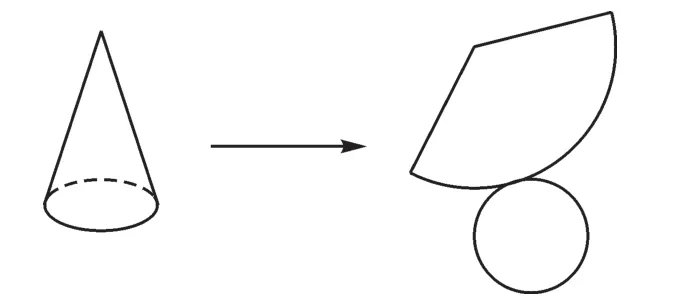
图3

4.棱锥的表面展开图.

棱锥的表面展开图由一个多边形（底面）和几个三角形（侧面）组成.三棱锥的表面展开图如图4，四棱锥的表面展开图如图5.

图4

图5

5.棱柱的表面展开图.

直棱柱的表面展开图由两个完全相同的多边形（底面）和几个长方形（侧面）组成.

直三棱柱的表面展开图由两个大小一样的三角形和三个长方形组成，如图6.

图6

图7

直四棱柱的表面展开图由两个完全一样的四边形和四个长方形组成，如图7.

二、几何体展开图

1.正三棱锥的两种展开图之间的关系.

不同几何体的表面展开图不相同，同一个几何体不同展开方式得到的平面图形也有所不同，但组成这些图形的基本图形往往又是一致的.

例如：将图8的正三棱锥沿AB、AC、AD三条棱剪开，得到的平面展开图为图9，若沿着AB、BC、AD三条棱剪开，得到的平面展开图为图10.

图8

图9

图10

上述两个三棱锥的表面展开图，虽然形状不同，但组成元素都是三角形.由此我们可以猜测由四个三角形组成的几何体的展开图可能是三棱锥.

无论是哪种形式的展开图，只要能将其围成一个立体图形，它就是该立体图形的平面展开图.

2.正方体的十一种展开图.

正方体的展开图详见本期第50页文章《借用口诀识记正方体展开图》.