基于广义交替数值通量的LDG方法求解Burger’s方程
张荣培, 王 迪, 刘 佳
(1. 沈阳师范大学 数学与系统科学学院, 沈阳 110034; 2. 沈阳师范大学 大学外语教学部, 沈阳 110034)
0 引 言
Burger’s方程在气体动力学、湍流、波的传播等研究中有着广泛的应用,该方程最初是由Bateman提出的,之后由Burger作为流体流动的数学模型定义为Burger’s方程。对于Burger’s方程的解析解,Hopf[1]和Cole[2]曾分别表明,在任何初始条件下,都可以用傅立叶级数的形式表示。然而,当初值不够光滑时,求精确解存在一定的困难。许多研究者已经研究出求解Burger’s方程的各种数值方法,如有限元方法[3]、有限体积法[4]、有限差分方法[5]等。
局部间断Galerkin(LDG)方法最初是由Cockburn[6]和Shu[7]在Bassi和Rebay针对Navier-Stokes问题所做工作的启发下提出。LDG方法具有一定的灵活性和优势,例如精度的阶数可以在每个单元网格中局部确定,所以可以很容易地被设计为任意阶精度。当然它也适用于复杂的网格区域和h-p自适应计算,并具有良好的并行化。正是因为该方法的这些特点,使其在实际计算中被广大研究者选用,例如:文献[8]是耦合的Burger’s方程对应的LDG方法;郑亚敏[9-10]针对一维常系数对流扩散模型方程,讨论了当含有Nuemann边界条件和Dirichlet边界条件时,局部间断有限元方法(LDG方法)的稳定性;谢珊珊[11]对非线性对流扩散方程的LDG方法进行了详细的误差估计;刘晓阳[12]对一维对流扩散方程LDG方法进行了超收敛性分析;许锦程[13]针对局部间断Galerkin方法关于非光滑初值作出了误差估计。对于LDG方法的构造,数值通量的合理使用能够保证系统的稳定性和高精度。以上文章中采用的都是纯粹的交替数值通量。在最近的研究中,Cheng[14],Meng和Zhang[15]构造了通过选取广义数值通量来求解对流扩散方程的LDG方法,并且在得到最优误差估计的基础上,构建和分析了新的广义Gauss Radau投影。
将局部间断Galerkin(LDG)方法应用于求解Burger’s方程,首先利用Hope-Cole变换将Burger’s方程转化为一个热传导方程,随后将其改写成含有一阶导数的等价系统;该系统Galerkin(DG)方法离散后可得到引入变量的解;最后,通过变换得到原方程的数值解。
1 问题描述及预备工作
1.1 Burger’s方程
考虑在初值条件u(x,0)=f(x),a ut+uux-vuxx=0 (1) 其中v是一个常数。 (2) 对应的初值条件即变为 (3) 对应的边界条件变为Nuemann边界情况即wx(a,t)=0,wx(b,t)=0。 其中:V=(P0(ξ),P1(ξ),…,Pk(ξ))T表示Legendre基函数;Wj(t)=(wj,0,wj,1,…,wj,k)T为上Ij的自由度,则在Ω上的自由度为集合Wj(t),即W=[W1;W2;…;WJ]。 (6) 由于是齐次Nuemann边界条件,因此2个边界点的数值通量的定义为如下形式 为了得到误差估计,选取2个广义Gauss Radau投影:对任意足够光滑的函数z,广义Gauss Radau投影Pθz定义了Pk(Ij)的唯一函数,满足 考虑到边界条件和跳跃项的定义,对式(4)和式(5)在整个区域上求和 对以上2式求和 (7) 其中 定理1(稳定性分析) 对于系统式(4)和式(5),利用LDG方法所得到的数值解在L2范数下是稳定的,即数值解wh满足‖wh(·,T)‖≤‖wh(·,0)‖。 证明 令vh=wh,qh=ph,并将其代入式(14)中得 对于式(9)右端第1项,进行分部积分有 利用数值通量的定义式(6),可以得到 通过以上推导可得到式(9)右端第2项的2种表达形式即 代入式(9)可以得到 B(wh,wh,ph,ph)=0 (10) 将式(10)的结果应用于式(7),可得到 即 由此可得出结论: 证明 令 是显然成立的,考虑式(7)、式(11)和式(12)可得 (13) 将vh=εw,qh=εp代入式(13)有 (15) 通过Cauchy-Schwarz不等式和Young’s不等式,可得 (16) 则根据Gronwall不等式、式(15)和式(16)可得到误差分析结果。 利用矩阵指数法来研究时间离散系统,式(4)和式(5)可以写成如下的矩阵形式 (19) W(0)=W0 求解Burger’s方程(1),初值条件为u(x,0)=sin(πx)0≤x≤1。 取J=25,分别取v=0.1,0.01,则可以得到在T=0.2,0.5,1.0,2.0时的数值解(图1)。 图1 当T=0.2,0.5,1.0,2.0时,分别取v=0.1和v=0.01所对应的数值解Fig.1 Numerical solution at different times T=0.2,0.5,1.0,2.0 for (a)v=0.1 (b)v=0.01 应用广义交替数值通量,通过LDG方法对Burger’s方程进行了求解。首先通过Hopf-Cole变换将非线性Burger’s方程转化为线性热方程;然后通过LDG方法对一阶常微分方程离散化;最后利用指数矩阵方法求解常微分方程组。通过对数值算例的数值结果进行仿真计算,证实了通过选取广义交替数值通量的LDG方法求解Burger’s方程是高度有效的。

1.2 计算区域剖分

1.3 相关定义
2 LDG方法

2.1 广义Gauss Radau投影

2.2 主要结果


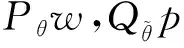
3 时间离散




4 数值算例


5 结 论

