直观呈现法下的乘法分配律教学

浙江东阳市白云中心小学（322100）

弗赖登塔尔认为：学习的最佳捷径是实践。通过二次创造获取的知识、形成的技能要比被动灌输接受，掌握得更牢固，提取运用时也更加及时顺利。弗赖登塔尔曾经说：“如果有可能，将学生置身于具体生动的情境中，进行直观地学习，学到什么是什么。不做任何强加解释，也不进行任何引导归纳，更不形成公式法则。”弗氏的直观教学法，令笔者茅塞顿开。

一、教材模式的不足

为了备好“乘法分配律”这一课，笔者参考了许多教案，发现一个普遍存在的做法，就是从猜想分配律公式到举例验证其合理性，通过完全归纳法概括出一般定律。苏教版教材四年级下册也是借助相关情境图来阐述分配律规则的：

第一步，从买5件皮夹克和5条长裤的总价入手，运用两种方法列出两个算式，然后用等号连接建立等式；

第二步，通过观察对比等式两边的算式形态，分析推导其中的逻辑关联，初步提出公式；

第三步，按照原型仿写算式，通过比较计算结果的大小，证实这种联系的普遍性；

第四步，用代数式表达规律。

这一学习流程，要求学生理性思维能力具有一定水准，思考问题细致周全、逻辑严谨，注意力长时间集中。然而面对这一学习流程，学生往往心绪不宁，焦躁不安，缺乏耐心，较易松懈。更为重要的是，从猜想到求证的过程中，学生的思维习惯是将等号左右两边的算式隔离后再分析，只关注结果的一致引起的相等关系，从结果一致反推出算式的相同。这一过程中，学生对分配律的认识是呆板和狭隘的，学生无法动态推演分配变化的过程，未能深入领会其真正的内涵，思维活动“程序化”就像是走过场。如此一来，学生也就无法在脑海里将分配律的外在格式和内在精要贯通起来，造成的后果是麻木地套用公式，这进一步加大了学习乘法分配律的难度。

二、直观式教学初探

1.复习引入

师（出示两个长方形，长和宽分别为4、3厘米和5、2厘米）：请求出图1中两个长方形面积之和。

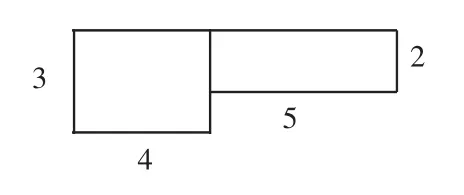
图1

生1：可以把两个长方形拼接起来，计算组合图的总面积。

师：大家按面积公式列式4×3+5×2后，计算可分三步，前两步先分别求出两个长方形的面积，再相加求总面积。

从长方形面积公式入手，将代数题型转化为直观几何题，在两个长方形面积之和的具体直观情境中，学生一步步经历乘法分配律的生成过程。

2.探索规律

师：现在对图形做一些变动，将第二个长方形的宽度变为3厘米。大家再列式求这两个长方形的面积之和。

学生很快列出算式并算出结果：4×3+5×3=12+15=27(cm2)。

师：大家做得很对，太棒了！那么还有没有不同的做法？现在数据变了，两个长方形的宽度相同，组合图的形状也发生了变化，第二次组合图与第一次组合图有所区别。

（学生分小组合作探究）

师：如图2，此时组合图从整体上看就是一个大长方形，两个长方形的宽度一样，都为3厘米，所以沿宽拼贴，刚好让长“共线”，于是新的长为4+5=9（cm），宽仍为3厘米，得出(5+4)× 3=27(cm2)。

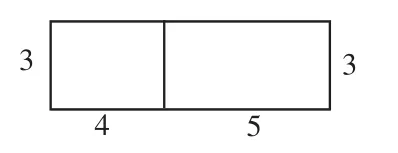
图2

师：回过头来看图1，能否使用新方法计算？

生2：不行！

师：仔细对比前后两幅图，知道其中的原因吗？

生3：图1中的两个长方形没有等长的边，无法组合成新矩形，而图2中两个长方形的宽度相等，导致长可以在一条直线上，刚好组合成一个新长方形。

师：如果将图1中的第二个长方形的长度稍作改变，使之解答可用新方法。该怎么改？

生4：将第二个长方形的长度由5厘米改为4厘米，这样就能将两个长方形的长合并起来，可以得到一个新的长方形（如图3）。

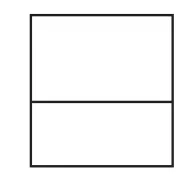
图3

列式：4 ×(3+2)=20(cm2)。

师：两种方法所求的是同一个大长方形的面积，也就是两个小长方形面积之和，于是得到4×3+5×3=(4+5)× 3，4 × 3+4 × 2=4 ×(3+2)。

师（指导学生认真观察等号左右两边）：下述哪个算式可以用第二种方法计算？判断后请作图检验。

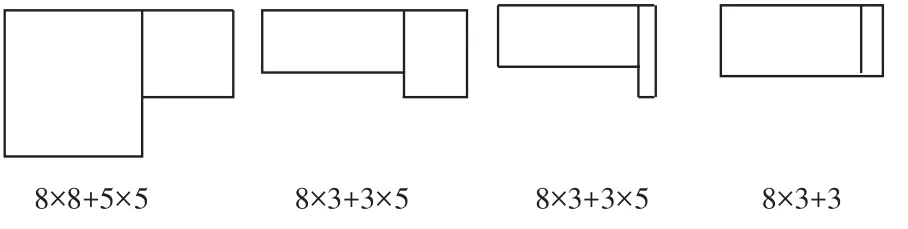
学生讨论、画图检验后，整理算式为：

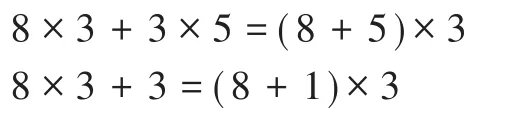
三、渗透数学本质

数学最本质的东西是抽象，抽象是创造的基础。

乘法分配律比交换律和结合律更加复杂。按照教材的设计思路讲授，学生就会将注意力分散于两种代数式上，不会深入反思为什么二者相等，是不是所有的面积组合都可以运用新方法计算。学生学习伊始就依赖于新算法，甚至执迷于新算法，丧失了继续深究与鉴别的动力。本课的设计改变了教材提出的由情境到猜想的模式，逐步出示两种方法，简单复习之后，马上提出形式相近的变式，学生立刻警觉：运用第二种算法是有前提条件的，那就是两个矩形必须有一条等长的公共边。对这一前提条件的清醒认识，有利于凸显分配律中左右两个算式的本质联系。

分配律的表述比较多，没有统一范式，因此学生总结分配律时就有很大的发挥空间。但无论哪种表达式，都少不了对其进行语言描述。教材将乘法分配律归纳为字母表示形式“(a+b)×c=a×c+b×c”，从举例验证到字母归纳，自始至终都是在数字演算上做文章，学生很容易沉沦在抽象思维的泥潭里。本课设计，从改变长方形的长和宽的长度引出两种面积算法，趁势引发学生思考哪种情形才适合用新方法，并借助画图操作与合理联想，赋抽象的“分配”予具体的几何线条，使枯燥的学习变得生动有趣起来。

现在的数学课堂因为过度追求理性思维，大幅缩减直观教学，软件演示代替了手工操作，理性推理代替了感性体验，学生思维负担增加，学习乐趣直线下降，这不得不引起教师的警惕和深思。