循“理”入“法” 以“理”驭“法”
——对“一个数除以小数”新授环节的实践与思考
浙江诸暨市海亮小学(311800)
教学“一个数除以小数”时,教师经常会有这样的困惑:如此简单的教学内容,学生作业的完成效果却常常不尽如人意,虽然后续可以通过加大练习题量的方式逐步提高学生作业的准确率,但是这样又落入了计算教学的一大“误区”。日前,笔者参与了教研组就这一内容进行的“同课异构”教学活动,针对其中的“新知探索”环节进行对比式课堂实践。
【第一次教学实践】
出示例题:奶奶编一个中国结需要0.85米丝绳,有7.65米长的丝绳,可以编几个?
读题后列出算式:7.65÷0.85=
师:这个题目与我们之前学过的知识有什么不同?(这题的除数是小数)你能用自己的方法试着算一算吗?

师:生1,你是依据什么转化的呢?
生1:商不变的性质。
师:生2和生3都是用竖式来解决,哪位同学的结果是正确的?
师:虽然生2的结果正确,但是列的竖式有问题。一起来看看老师是怎么做的。(一边板书过程,一边讲解示范)
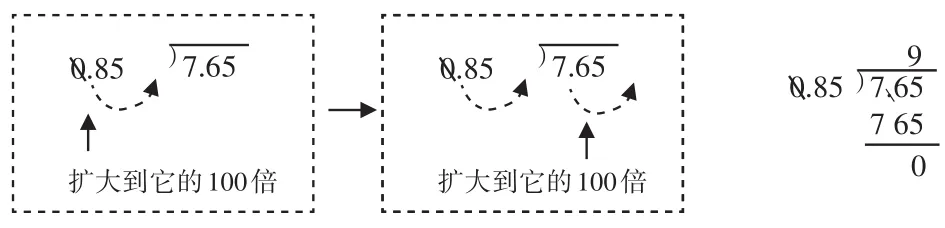
师:你能用这种方法再计算一遍吗?(学生练习)请生4说说你的想法。
生4:我把米转化成厘米,这样就可以转化成整数除法来解决。
师:这其实与生1的方法相同。计算除数是小数的除法,先利用商不变的性质将它转化成除数是整数的除法,所以要先看除数的小数位数,然后将被除数同时扩大相同的倍数。
教师列式后放手让学生去计算,必然会出现各式各样的解题方案,一旦涉及竖式计算过程,更会产生大量的可以利用的“错误资源”。此时,教师的主导作用已经演化为在处理各种算法中逐步落实本课的知识目标。然而,正是这种看似通过自主探索,使学生经历了算法多样化和过程优化的教学方法,却为后续实际教学效果不佳的状况埋下了“地雷”。
深入探索其中的原因,在以上环节中,学生需要在教师的引导下同时解决“该怎样算”“为什么这样算”“还可以怎样算”“怎样算更好”四个问题,其中前两个问题指向“计算依据”,后两个问题则体现了“计算方法”。正因为承载的内容和目标过多,难免会产生学生对“计算依据”理解不透彻,对“计算方法”掌握不扎实等现实问题,从而陷入“儿童急走追黄蝶,飞入菜花无处寻”的困境。
基于这些思考,笔者对这一个环节进行了再次设计。
【改进后的教学过程】
1.创设情境,比较设疑
逐题出示以下三个问题,分别列式并板书:(1)编一个小号的中国结需要35厘米丝绳,有735厘米丝绳,可以编几个?(2)编一个中号的中国结需要61厘米丝绳,有561.2厘米丝绳,可以编几个?(3)编一个大号的中国结需要0.85米丝绳,有7.65米丝绳,可以编几个?
师:这三个题目有什么共同点?(都是求“可以编几个”的问题,用除法计算)在得出的三个算式中,如果让你选择一题计算,你会选择哪一题?为什么?
生1:735÷35。这题的被除数和除数都是整数。
师:也就是整数除法。剩下来的题目中,你会选哪题呢?
生2:选561.2÷61。这题的除数是整数,我们已经学过除数是整数的除法。
师:这两个算式有什么共同点?
生3:都是除数是整数的除法。
师:只要除数是整数就可以了?被除数是小数对于你们来说有没有问题?(没有)
师(指7.65÷0.85):为什么不选这个算式呢?
生4:这题的被除数和除数都是小数。
师:主要是因为谁是小数?(除数)跟另外两题相比,它属于除数是小数的除法。
2.巧用转化,理解算理
师:有两题的解法是我们已经学过的,有一题的解法是没有学过的,对于没有学过的,你有什么想法?
生5:可以把除数是小数的除法转化成除数是整数的除法。也就是把没有学过的知识转化成已经学过的知识来解决。
师:这个想法非常好!那么,大家想到转化的方法了吗?

图1
师(板书如图1):说说这是怎么想的。
生6:把被除数和除数同时扩大100倍,商不变。
师:为什么这里是乘以100而不是其他的数呢?
生7:要把除数的小数转化成整数,除数是两位小数,所以扩大100倍。
师:也就是说,这种转化是由谁决定的?(除数)具体一点呢?(除数的小数位数)对被除数是怎么处理的?(除数扩大多少倍,被除数也扩大多少倍)
师:还有别的转化方法吗?(板书如图2)说说你的想法。
生8:可以把m转化为cm后再计算。
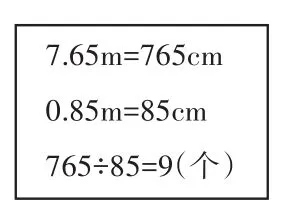
图2
师:非常好,把m转化为cm,其实就是把被除数和除数都转化成整数,也可以看作是利用了商不变的性质。
3.建立联系,竖式计算
师:这个过程如果用竖式,该如何表示呢?我们一起来试一试。(竖式表示中再次强调“算理”;过程略)
可见,第二个环节的教学中重点强调了计算这类题目之前进行转化的发起点是“除数”,实施关键则是“除数的小数位数”。由于课堂练习中已经出现了“被除数的小数位数比除数多”的变式(0.544÷0.16),此时引入例5“被除数的小数位数比除数少”的教学就水到渠成了。
【新增例5的教学】
师(出示例题:12.6÷0.28):仔细观察,这题和前面的题目有什么不同?
生9:被除数的小数位数比除数少。
师:那怎么办呢?谁来说说你的想法?
生10:将除数转化为整数扩大了100倍,被除数也要扩大100倍。
师:被除数扩大100倍以后是多少?你是怎么想的?
生11:位数不够,在末尾用0补足。
师:这样就转化成了怎样的一个算式?(整数除以整数)大家能把刚才说的过程用竖式表示出来吗?在草稿本上试一试。(学生练习、反馈,教师讲评,再次强调“先看除数的小数位数,再进行转化”的知识要点)
师(小结):被除数和除数的小数位数相同,被除数小数位数少于除数,都可以转化为整数除以整数;被除数小数位数比除数多的时候,可以转化为小数除以整数。
相比于第一次实践的思路,改进后的设计和实施有效避免了“计算依据”与“计算方法”混淆的现象,突出体现了以下两个方面的教学意图。
一、构筑起完整的教学体系,始终遵循从“计算依据”中导入“计算方法”
课始创设的一个简单情境,就引出了三种不同类型的算式,通过“你会选择哪一题计算”的问题,带领学生回顾了“整数除以整数→小数除以整数→一个数除以小数”的知识学习过程。在教学两个例题的过程中,坚持以对“算理”的深入理解为先,再顺势导入用竖式计算的方法。
在教学例5之后,引导学生依据板书自主探索“所学新知”与“已有旧知”之间的关联,帮助学生构建较为完整的知识体系。这种以知识的内部联系去促进学生理解的方式,对应了《浙江省中小学学科教学建议(小学数学)》中提到的“教师要善于运用‘联系观’去改变教学深度”的观点。小学数学中计算教学内容“螺旋上升式”的编排方式,自始至终都隐含着“体系化”的属性,在日常教学中,教师只要善于挖掘和利用,必将对学生理解算理和掌握算法起到非常重要的推动作用。
二、经历知识形成过程,特别强调以“计算依据”驾驭“计算方法”
“怎样算”“为什么这样算”“还可以怎样算”“怎样算最好”这四个问题,清晰地阐述了计算教学中新知探索环节的主要步骤。只有切实地解决了前面两个指向“计算依据”的问题,才能奠定习得“计算方法”的知识基础。单就“除数是小数的除法”这一内容而言,似乎存在“算理”和“算法”之间的区别不是非常清晰的情况,毕竟用横式解决的方法也可以看作是一种具体的算法。实际上,这正好顺应了对“怎样算最好”这个问题的解决,也就是进一步的算法优化——列竖式计算。
值得一提的是,在竖式计算的具体过程中,特别强调以除数的“小数位数”为转化的“起点”,被除数的“小数位数”随除数发生的变化而变化。这样的教学设计,一方面合理地搭建了“计算依据”与“计算方法”之间的桥梁,另一方面,也充分体现了前者对后者的“驾驭”作用。

