拨『乱』反『正』，提高计算正确率

江苏省张家港市梁丰小学 钱晓燕

在小学数学教学内容中，占比例最大的是数的认识和数的运算，这两个内容起着举足轻重的作用。但是小学生算错题却是经常出现的情况。对此，我们不能简单地把这种问题归咎于学生的粗心马虎，应该帮助学生分析错误的原因，采用恰当的策略“拨乱反正”，寻求事半功倍的教学方法。下面，就以学生计算错误的原因及引导纠错的策略进行剖析。

一、计算方法，理解中掌握

算理是计算数学的灵魂。计算法则的理解和掌握是小学数学计算教学的首要任务，通过观察、操作、探究，让学生理解算理。同时，教师也应挑选出学生在练习过程中出现的典型错例，引导学生共同分析错误原因，既能帮助学生把错误消灭萌芽状态，也能使学生知其然更知其所以然。

以52×31的竖式计算为例，摘录学生错解，如图1、图2。可以看出学生的错因是用第二个因数中的3去乘2，得到的积末位应写在哪里？为什么？这是学生最易出错的地方，也是本课重难点所在。为此，我从算式的意义和直观情境图入手，引导学生从位值制思想去理解“算理”，从而理解乘数中每个数相乘时各自应写在什么位置上，如图3所示。消除学生的困惑，帮助学生真正理清算法，突破本课教学重难点，即“十位上的数依次去乘第一个因数每位上的数”的计算方法。

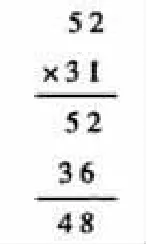
图1

图2

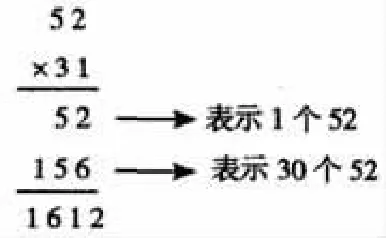
图3

在教学中，教师应及时捕捉在课堂学习过程中的各种生成性教学资源，在思维障碍处予以点拨引导，提前进行干预，帮助学生拨开思维的迷雾，获得发展。

二、加强对比，减少负迁移

奥苏泊尔认为，知识迁移就是人们已有的认知结构对新知识学习发生影响。而如果已知的知识技能对学习的新知识技能产生干扰，起消极阻碍的影响，称为负迁移。因此，教师应重视负迁移带来的消极效应，尤其是对于容易混淆的计算问题，更需要克服定式思维，通过辨析、纠错等活动突出新知识的内涵、特征和规律，提升学习效率。

例如，由于负迁移而出现的较为典型的错误：1.25×8÷1.25×8=1；100÷25×4=1。究其原因，学生因为受到简便计算 125×8=1000，25×4=100 思维的影响，再进行四则运算的练习时往往就会受到相似信息的影响，原有的简便计算思维自然浮现，而干扰了对运算顺序的思考，导致学生忽视了“同级计算从左往右依次计算法则”的计算法则。针对此类易错题，教师可以有针对性地设计对比练习题，提前干预学生可能产生的思维误区，如判断以下计算题：

①191-45+55=191-（45+55）；

②62+38×3=（62+38）×3；

③25×（4×8）=25×4+25×8。

第一道习题，意在提前干预连减简便计算与加减混合运算的混淆；第二道习题，意在提前干预乘法分配律受加减混合运算的混淆；第三道习题，意在提前干预乘法分配律与结合律的混淆。通过对典型错题的议错、辨错活动，使学生有序重建正确的知识结构，摆脱负迁移的不良影响。

三、收集错题，反思中领悟

错题集是学生将自己平时的考试、练习、作业中的做错的题目进行的一种系统汇总，建立一个错误档案。对错题集进行合理的整理、反思和利用，可以帮助学生吸取前车之鉴，有针对性地复习补救，提高数学思维品质和能力。

例如，针对六年级圆柱体积的计算，有学生收集错集如下：

题目：图书馆门前建了两个同样大小的圆柱形花坛。花坛的底面直径为6米，高为0.9米，往里装泥土的高是0.7米，两个花坛中共需要填土多少方？

错解 1：3.14×（6÷2）2×0.9×0.7×2

错解 2：3.14×（6÷2）2×0.9×2

错解 3：3.14×（6÷2）2×0.7

错因分析：这道题目中求的是共需要填土多少方，而不是求花坛的体积，题目中“花坛的高为0.9米”为多余信息。错解1和2，都是因为习惯了常规性圆柱体体积的求解，认为圆柱的半（直）径和高为必要条件，导致分不清有用与无用信息。错解3是由于未看清题目所求的是两个花坛的填土量。在以后的解题过程中，我会养成仔细读题，分析题目的有用信息和干扰信息的好习惯。

错题集的收集，就是记录纠错的心路历程，帮助学生及时归纳和总结学习中的易错知识点，加深理解和掌握，帮助学生提升学习效果。

总之，学生的错误在所难免，同时也在检验着教师教学有效性。面对学生的错误，需要我们有的放矢地干预和跟进，辨析错因，以自己的教学智慧帮助学生“少错、无错”，通过“避错”“纠错”等教学活动，引导学生领悟计算方法，发展计算思维。