锁销位置对折叠翼固有振动特性的影响分析

黄 俊，宋保江，宫钇成，郑 榕，阎绍泽

（1. 空间物理重点实验室，北京，100076；2. 清华大学机械工程系，摩擦学国家重点实验室，北京，100084）

0 引 言

折叠翼技术是现代飞行器如航母舰载机、弹道导弹等军事装备中有待进一步发展的先进技术之一。对于弹道导弹而言，采用折叠翼技术能够缩小弹体的横向尺寸，易于导弹发射，减少储运空间，增加舰艇或车辆的运输能力，对提高军事装备的战斗力具有重要意义。

鉴于航母舰载机、导弹等高精尖军事装备对折叠翼技术的迫切需求，国内外学者已对折叠翼结构的方案设计、展开运动学与动力学等方面进行了研究。Kroyer[1]采用有限元方法分析了某型号导弹折叠翼的折叠状态及展开过程的可靠性问题，但并未分析展开状态下的折叠翼振动特性。Peter等[2]通过试验研究和理论计算对不同机翼折叠角情况下折叠翼系统的气动弹性响应特性进行了分析。Snyder等[3]利用有限元的方法在不同的折叠翼折叠角度、刚度和自重等条件下，研究了折叠翼的固有频率的敏感度和颤振不稳定性，提出了减振、避振的方法。此外，有些学者研究了智能材料和智能结构等新型材料及结构应用于折叠翼结构的问题，以期达到加强或优化折叠翼结构性能的目的[4～10]。谭湘霞等[11]针对折叠翼的展开过程，设计了具有通用性的折叠翼展开动力学分析仿真模型。倪健等[12]应用失效模式和影响分析的方法对某型导弹折叠翼展开机构的可靠性进行了较为全面的研究并得出了可靠性分析模型。陈鹿民等[13]对含间隙的空间可展结构进行试验研究，讨论了连接间隙对可展结构动态特性之间的关系。李毅等[14]对折叠翼的折叠过程中的颤振进行了仿真分析，探究了折叠角及作动器刚度对折叠翼颤振特性的影响。杨宁等[15]建立了多自由度结构非线性折叠翼气动弹性方程的子结构方法，研究分析了折叠翼翼面的颤振特性。

折叠翼展开后的锁定问题是影响翼面展开后刚度的关键。若用传统的柱销锁定方式，不可避免存在间隙非线性问题，由于内外翼板的锁定冲击作用，将激起持续的折叠翼振动。为此，本文设计了锥销锁定式折叠翼结构，研制了折叠翼试验装置，通过折叠翼振动试验和有限元模拟方法，分析了内外翼之间采用不同锥销锁定组合下的折叠翼固有频率及振型，给出了较佳的内外翼锁销布置方案。

1 折叠翼结构与试验设计

1.1 折叠翼结构样机

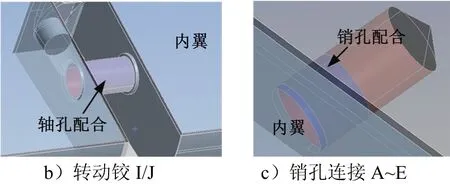
锁销连接折叠翼结构如图1所示。本文研制的折叠翼由内翼、外翼两部分组成，该折叠翼有A～E共5个位置可以布置销孔连接，销、孔均为锥形，销轴由弹簧压紧在外翼的锥孔中，以保证销孔之间的配合无间隙，如图1a所示，材料选用2A14铝合金。折叠翼的内翼和外翼通过转动铰I、J相连接，以使外翼可以相对内翼转动，如图1b所示。折叠翼展开后，内翼与外翼通过锥销锁紧，如图1c所示。在完成折叠翼内、外翼的装配后，折叠翼的总体尺寸为：长550 mm，宽380 mm，高38 mm。

续图1

需要说明的是，折叠翼样机结构设计忽略了翼面驱动和传动机构的布置，这是因为本文研究内容是锁销位置对翼面刚度的影响规律，而简化驱动和传动机构不仅不改变此影响规律，还消除了过多连接环节累积到翼面刚度试验结果中的误差。

1.2 锁销组合的试验设计

本文旨在通过试验研究不同锁销连接组合下折叠翼固有振动特性的差异，以确定折叠翼较佳的锁销位置。在样机结构设计中，5个锁销可以组合使用，也可以单独使用。如表 1所示，第 1组锁销组合方式为5个位置同时装配圆锥销，展开后折叠翼结构具有最大的连接刚度。

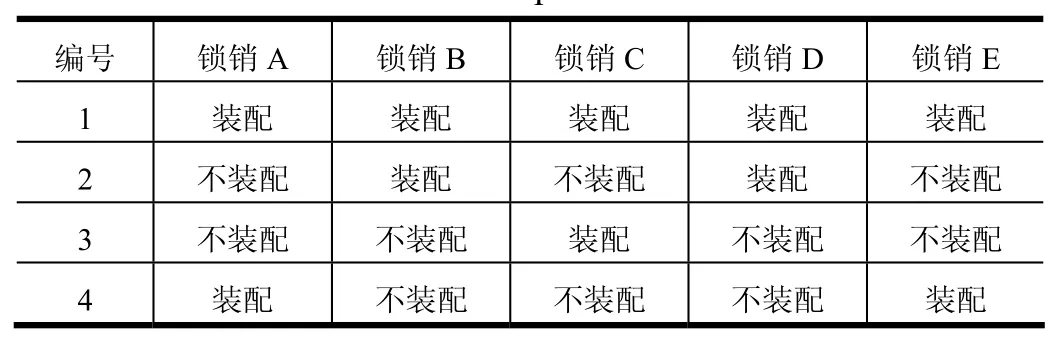
表1 锁销连接结构组合Tab.1 The Case Description of the Pin Position

考虑到锥销数量过多会增加系统复杂度，降低锁定动作可靠性，因此实际锁销设计会减少销钉数量。此外，锁销在翼面上的布置应具有对称性，所以第2、3、4组的组合方式分别是BD锁定、C锁定和AE锁定。后3种组合方式是折叠翼结构最可能选用的锁定位置方案。

1.3 测试系统及测试方法

包含内翼和外翼的折叠翼结构是一个多刚体系统，本文旨在研究锁销位置对折叠翼刚度特性的影响。考虑到折叠翼在飞行器的固支结构形式是多样的，选择固支模态试验方式难以反映内外翼连接环节的一般特性，因此，采用自由模态进行固有刚度特性分析。图2给出了锤击法测量折叠翼固有模态的流程。

由于锤击法要求折叠翼的支承模态应远低于第 1阶弹性模态频率，故选用汽车内胎作为折叠翼的支撑。在调整支撑位置选择时，选择在试验中折叠翼振幅较小的位置作为支撑位置。根据翼面的结构形式，选择折叠翼激励点及测量点。本试验采用多点激励，图 3为折叠翼自由模态试验测试系统的实物。图3a中的折叠翼激励点网格，其中内外翼各有16和52个敲击点，网格式的激励点选择有助于反映构件的整体构型。在折叠翼的对角位置分别布置了两个加速度传感器，用来测量每次敲击后所激发的加速度信号；采用 LMS SCADAS Ⅲ型动态采集系统对加速度信号进行采集，并利用 LMS Test Lab软件中的最小二乘复频域法（PolyMAX方法）进行模态参数识别并最终得出折叠翼的固有模态。

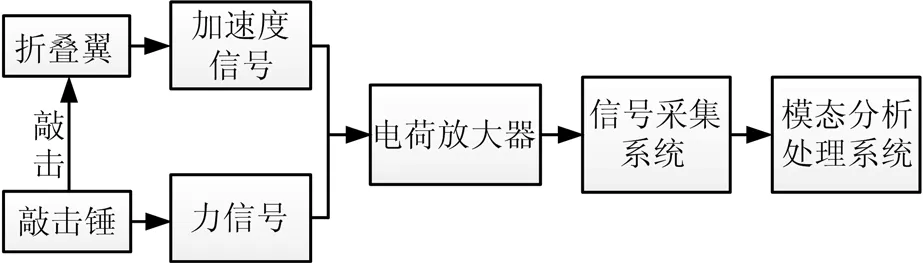
图2 锤击法测量模态流程Fig.2 Flow Chart of the Hammer Excitation Experiment to Obtain the Modal Information

图3 折叠翼自由模态试验系统Fig.3 The Modal Experiment System of the Folding Wing

2 折叠翼自由模态试验结果分析

在完成折叠翼模态试验的支撑方式、测点及激励点的选择、传感器安装后，启动LMS Test Lab软件并依次完成通道选择、锤击调试设置、带宽设置、加窗设置等步骤，然后开始对折叠翼的自由模态进行试验测量。

通过锤击模态试验，可得到各试验组已展开折叠翼的前4阶固有频率与振型。图4给出了第1种锥销组合方式的折叠翼幅频响应曲线及前4阶固有振型。由图4a可以看出，弹性支承使得折叠翼刚体振型的固有频率不再为0，但是锤击试验所激起的刚体振型的固有频率在50 Hz以内，远小于折叠翼的第1阶弹性模态的固有频率269 Hz。因此轮胎弹性支承可以在折叠翼自由模态试验中模拟自由支撑的边界条件。由图4b可以看出，第1种锥销组合方式的折叠翼的前4阶固有振型分别为：1阶扭转振型、2阶沿翼面弦向的弯曲振型、3阶沿翼翼面展向的弯曲振型，以及4阶2阶扭转振型。

分别按照表1中给出的锥销组合方式进行折叠翼自由模态试验，得到在自由边界条件下折叠翼的前 4阶固有频率，如图5所示，表2给出了折叠翼前4阶固有频率的数值。

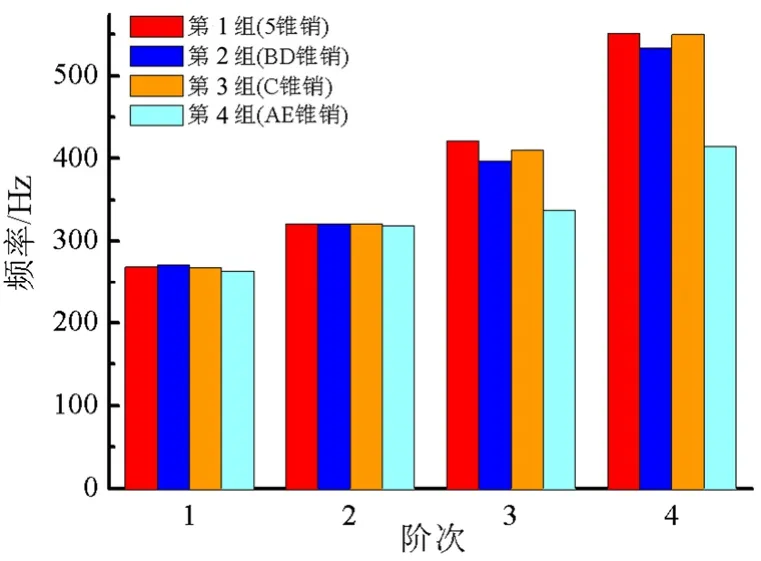
图5 四组折叠翼前4阶固有频率对比Fig.5 Comparison of the 4 Inherent Frequencies of the Four Cases

试验结果表明，4组试验结果的前两阶频率值相近，因此，折叠翼第1阶和第2阶振型与内外翼锁销连接结构关系不大，从图4所示振型也可侧面验证。

4组试验结果的后两阶频率值出现了差异，其中第3组（位置C处安装锥销）和第2组（位置B、D处安装锥销）与第1组锥销组合方式（5个位置均安装锥销）相比，后两阶固有频率相差均在6%以内。另外，第1、2、3组锥销组合方式的前4阶振型也基本一致。这表明，在C处安装锥销与B、D处安装锥销在锤击试验的激励量级下可以较好地保持折叠翼的固有振动特性。

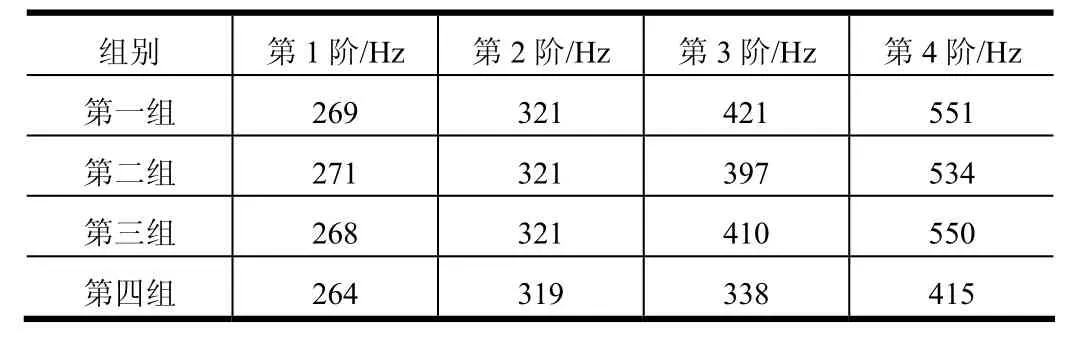
表2 折叠翼模态试验前4阶固有频率值Tab.2 The 4 Inherent Frequencies of the Folding Wing

第4组（A、E处安装锥销）的折叠翼前两阶固有频率与第1种锁销组合方式的相差较小，但后两阶固有频率却相差较为明显；而且第4组结构的后两阶振型与第1组并不一致，第4组的第3阶振型为内外翼沿翼面弦向的反向弯曲振型，该振型也出现在内外翼之间不安装锥销（即内外翼之间可自由翻转）的状态下。

3 折叠翼有限元分析

采用Pro/E软件建立如图1所示的折叠翼三维模型，将模型导入Workbench软件中。在Workbench中，定义折叠翼三维模型中材料和接触形式。选择铝合金材料，其杨氏模量为71 000 MPa，泊松比为0.33；定义内外翼间的锁销与孔配合接触面，接触面间采用固结连接。这是因为锁销采用弹簧预紧的圆锥销结构，锥销与孔的配合间隙可忽略；此外在翼面受到振动激励时，锁销仅受到径向力作用，因此锁销与孔之间没有相对运动。

由于折叠翼内外翼连接处的构型较为复杂，故采用自动划分（Automatic）的网格划分方法，该方法对规则的几何部分采用六面体单元，对不能被扫掠的部分则采用四面体单元。网格划分越细致，计算结果的误差越小，但是计算所需要的时间也越长，在逐渐细化网格的过程中，当前后两次仿真得出的固有频率数值之间的差异不超过百分之一时，则不再继续细化网格。边界条件设置为自由边界，本文分别对第 1组和第3组锁销装配方式的折叠翼结构进行模态计算，图6和图7分别给出了有限元模态计算得出的固有频率对比图与折叠翼前4阶固有振型图。

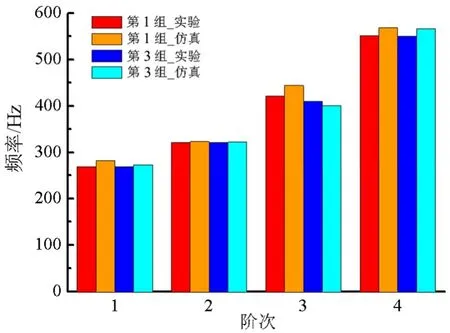
图6 第1组和第3组方案前4阶固有频率的仿真与试验结果对比Fig.6 Comparison of the Experiment and Simulation Results of Case 1 and Case 3 Inherent Frequency

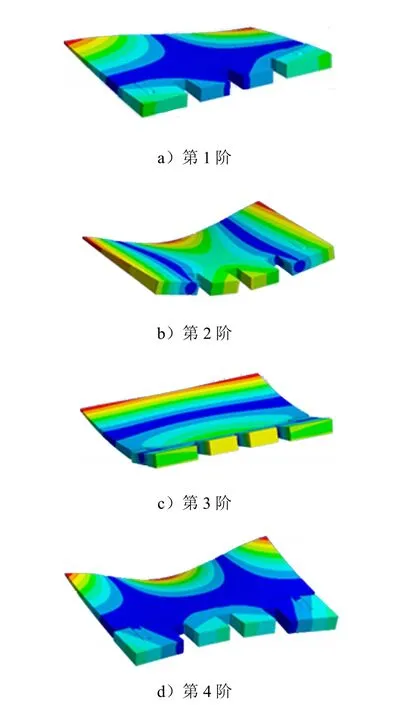
图7 第1种锥销组合折叠翼模态仿真前4阶固有振型Fig.7 Case 1 Simulation of the Four Vibration Modes

由图6和图7可以看出，折叠翼前4阶固有频率的仿真计算结果与试验结果误差在5%以内，各阶固有频率所对应的振型一致。这表明采用有限元方法可以模拟锥销锁定式折叠翼固有振动特性，也说明了试验结果是可信的。

4 结 论

本文设计了锥销锁定式折叠翼结构，通过折叠翼模态试验和有限元模拟方法，分析了内外翼之间采用不同锥销锁定组合条件下的折叠翼固有频率及振型。

试验结果表明：折叠翼内外翼间锁销连接的位置会对折叠翼固有振动特性（第3阶和第4阶振型）产生显著影响，锁销位置宜均布于内外翼连接界面上，增加内外翼连接刚度。未考虑间隙的有限元模型仿真结果与试验结果相近，侧面验证了锥销配合间隙在模态分析中可忽略。

通过模态试验方法评估了锥销位置对折叠翼刚度的影响，分析了折叠翼采用不同锥销位置结构方案时翼面固有频率和振型的响应，反映了内外翼连接装配环节对翼面在飞行器振动环境中响应的影响。结果表明，折叠翼锁销均布在内外翼连接界面时，内外翼之间有连续的连接，结构谐振频率更高。基于模态试验的折叠翼刚度评估方法简便易行，可用于折叠翼等可变形机构概念设计阶段的参数选型和优化。